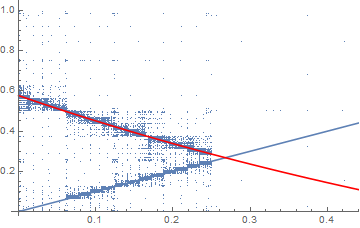
I dont know a fix, but at least its intersting to see whats going on: Start with the problematic case:
pts = Reap[ 2 NIntegrate[ Boole[ArcTan[x] + ArcTan[y] <= Pi/6 && x <= y], {x, 0, 1}, {y, 0, 1}, EvaluationMonitor :> Sow[{x, y}]]] Show[{ListPlot[pts[[2, 1]]], Plot[x, {x, 0, 1}], ContourPlot[ArcTan[x] + ArcTan[y] == Pi/6 , {x, 0, 1}, {y, 0, 1}, ContourStyle -> Red]}] You see the sampling scheme treats your Boole as a black box and does a huge number of evaluations hunting for the boundary.
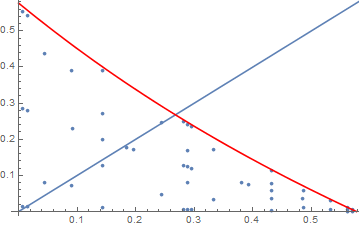
Now look at the simpler expression:
pts = Reap[ 2 NIntegrate[ Boole[ArcTan[x] + ArcTan[y] <= Pi/6 ], {x, 0, 1}, {y, 0, 1}, EvaluationMonitor :> Sow[{x, y}]]]; Show[{ListPlot[pts[[2, 1]]], Plot[x, {x, 0, 1}], ContourPlot[ArcTan[x] + ArcTan[y] == Pi/6 , {x, 0, 1}, {y, 0, 1}, ContourStyle -> Red]}] Evidently NIntegrate analytically recognizes the simple Boole expression and so automatically only samples over the appropriate region. Since the value is 1 everywhere it returns quickly with very few samples.
The same issue arises for the full area case if you set Method -> {Automatic, "SymbolicProcessing" -> False}