For a ellipse $E(\theta)$, which owns the parametric equation as follows:
$\begin{cases} x = a \sin\theta + b \cos\theta + c \\ y = d \sin\theta + e \cos\theta + f \\ \end{cases}$
Now, I have a point $P=\{x_p,y_p\}$, to know the relationship between $E(\theta)$ and $P=\{x_p,y_p\}$, I using this method:
$$ \begin{cases} \sin \theta =\frac{(c-x_p)e+b(y_p-f)}{b d-a e}\\ \cos \theta =\frac{(-c+x_p)d+a(f-y_p)}{b d-a e} \end{cases} $$
compute $m=\sin^2 \theta+\cos^2 \theta$
- if $m=1$, the point $P$ on the ellipse $E(\theta)$
- if $m>1$, the point $P$ outside the ellipse $E(\theta)$
- if $m<1$, the point $P$ inside the ellipse $E(\theta)$
However, for the compound curve, for example
ellipse segment $E_1(\theta) \qquad \theta \in [0, 2.4798],[5.8629, 2 \pi]$
ellipse segment $E_2(\theta) \qquad \theta \in [3.1275, 6.1325]$
line segment $L(E_1(2.4798),E_2(3.1275))$
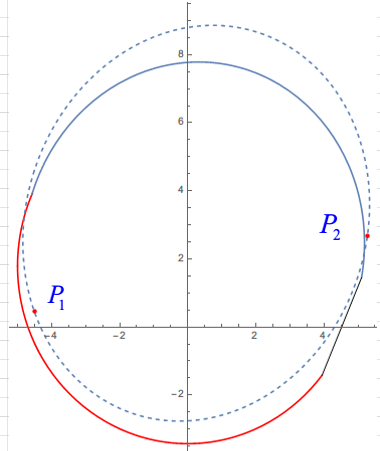
mat1 = {{0., -5., 0}, {-5.2203, 0., 1.7945}}; mat2 = {{-0.8583, -4.9384, 0.1765}, {-5.4189, 0.7822, 2.3088}}; θ1 = 2.4798; θ2 = 3.1275; Show[ {ParametricPlot[ mat1.{Sin[θ], Cos[θ], 1}, {θ, 0, 2.4798}, PlotStyle -> Red], ParametricPlot[ mat1.{Sin[θ], Cos[θ], 1}, {θ, 5.8629, 2 Pi}, PlotStyle -> Red], ParametricPlot[ mat2.{Sin[θ], Cos[θ], 1}, {θ, 3.1275, 6.1325}], Graphics[ {Line[{mat1.{Sin[θ1], Cos[θ1], 1}, mat2.{Sin[θ2], Cos[θ2], 1}}]}]}, PlotRange -> All] 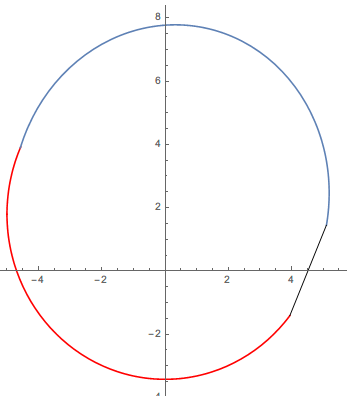
Now, I have two points $P_1,P_2$, whose coordinate are {{-4.50722, 0.455707}, {5.2748, 2.68502}},respectively.So I would like to know is there a simple method to determine whether $P$ inside the boundary?