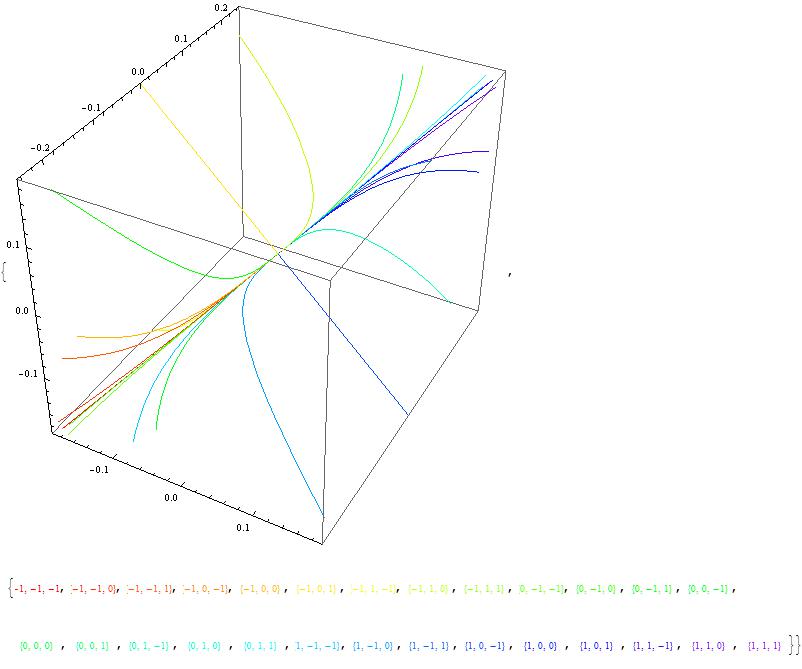
Here one way to plot many solutions for different C1, C[2], C[3].
dsol = DSolve[ Thread[{x1'[t], x2'[t], x3'[t]} == {{-2, 1, 0}, {1, -2, 1}, {0, 1, -2}}.{x1[t], x2[t], x3[t]}], {x1, x2, x3}, t] // FullSimplify; Since I work with MMA 8.0, I had to construct my own PlotLegend.
{ParametricPlot3D[ Evaluate[({x1[t], x2[t], x3[t]} /. First@dsol) /. Evaluate[ tab = Flatten[ Table[Thread[{C[1], C[2], C[3]} -> {i, j, k}], {i, -1, 1}, {j, -1, 1}, {k, -1, 1}], 2]]], {t, -1, 10}, PlotStyle -> Table[Hue[.8 (i - 1)/Length[tab]], {i, 1, Length[tab]}], ImageSize -> 300]500], Table[Graphics[{Hue[.8 (i - 1)/Length[tab]], Text[{C[1], C[2], C[3]} /. tab[[i]]]}, ImageSize -> 45], {i, 1, Length[tab]}]}