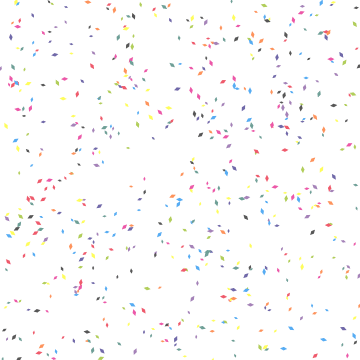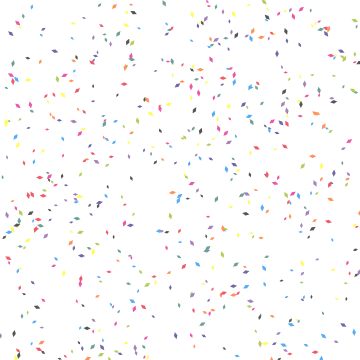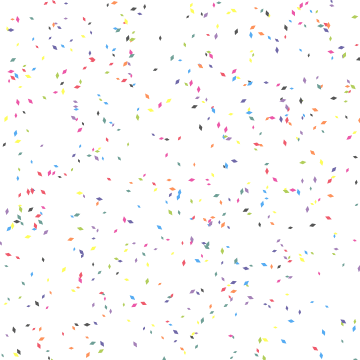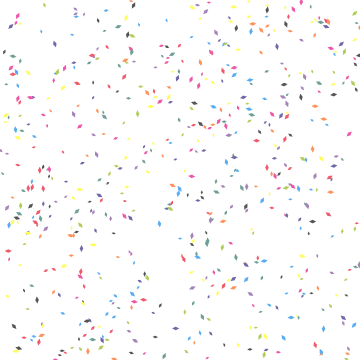No fluid dynamics I'm afraid, but here's what I came up with
Preliminaries
n = {200, 200, 200}; dim = 2; edges = {.015, .018, .024}; speed = {{0, -1}, {0, -1.5}, {0., -2}}; basePoly = {{0, -1}, {1/2, 0}, {0, 1}, {-1/2, 0}}; period = 3; Initial position colour and orientation
angularVelocity = N[RandomChoice[Range[-8, 8], #] period Pi] & /@ n; initPos = RandomReal[dim, {#, 2}] & /@ n; initAngle = RandomReal[2 Pi, #] & /@ n; colorcolors = Map[Lighter[ColorData[3][#]] &, RandomInteger[{1, 20}, #] &Transpose[ConstantArray[Hue /@ nRandomReal[1, {2}];200], 4]]; Some function to generate one confetti ( == confettus?)Visualisation
pos[pos0_,polygons[t_] ang0_,:= angVel_, col_, layer_][t_]Graphics[Table[ := Polygon[Function[{colpos, ang, vel}, Polygon[Mod[pos0 Mod[pos + speed[[layer]]speed[[i]] t, 2] + # & /@ ((edges[[layer]]edges[[i]] basePoly).RotationMatrix[ ang0 + angVel t])]} Visualisation
Manipulate[Graphics[Table[ ang pos[##,+ i][t]vel &t])] @@@ Transpose[{initPos[[i]], initAngle[[i]], angularVelocity[[i]]}], color[[i]]}], VertexColors -> colors], {i, 3}], PlotRange -> {{0, dim}, {0, dim}}]]; Manipulate[polygons[t], {t, 0, period - .03, .03}] Or to get an animated gif (note that exporting takes quite some time)
tab = Evaluate@Table[Graphics[Table[ pos[##, i][t] & @@@ Transpose[{initPos[[i]], initAngle[[i]], angularVelocity[[i]], color[[i]]}], {i, 3}], PlotRange -> {{0, dim}, {0, dim}}]Table[polygons[t], {t, 0, period - .03, .03}]; Export["confetti2.gif", tab]