See if the following will do what you desire. It first estimates the distance as half the distance to the nearest neighbor, and then splits the differences with the closest circles.
pts = RandomReal[{0, 10}, {100, 2}]; nf = Nearest[pts -> Automatic]; dist = EuclideanDistance[#, pts[[Last@nf[#, 2]]]]/2 & /@ pts; dist = FixedPoint[Function[{dist0}, 1/2 (dist0 + Table[Min[EuclideanDistance[pts[[i]], pts[[#]]] - dist0[[#]] & /@ Rest@nf[pts[[i]], 100]]Length[pts]]], {i, Length[pts]}])], dist]; // Timing (* {2.019525, Null} *) Graphics[{MapThread[Circle[#1, #2] &, {pts, dist}], Red, Point[pts]}] 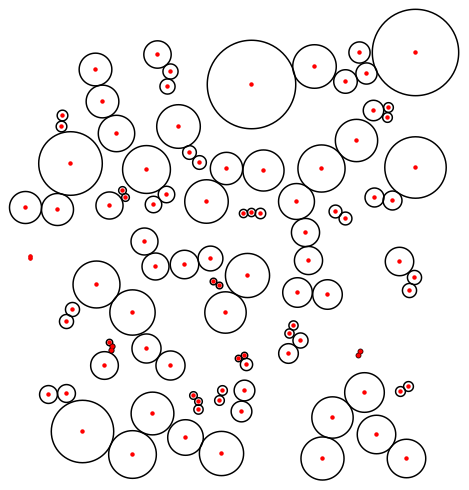
[Note: What might look like an isolated point on the left is actually two points close together.]
Quite a bit faster, but not very fast. Practically, though it is highly unlikely you have to test all points, only some of the nearest neighbors (here 9):
data = EuclideanDistance[#, pts[[Last@nf[#, 2]]]]/2 & /@ pts; dist = FixedPoint[Function[{dist0}, 1/2 (dist0 + Table[Min[EuclideanDistance[pts[[i]], pts[[#]]] - dist0[[#]] & /@ Rest@nf[pts[[i]], 10]], {i, Length[pts]}])], dist]; // Timing (* {0.254985, Null} *) The output is the same in this case. Of course there's no guarantee that the nine nearest neighbors will prevent overlap.
If you want the isolated pairs not to have the same radii, then you can start with
dist = RandomReal[{0.735, 10.47}] EuclideanDistance[#, pts[[Last@nf[#, 2]]]]/2 & /@ pts; And there will be a chance the radii will be significantly different. The lack of symmetry might be more visually appealing, depending on your intended purpose.
