Trying to solve the following PDE with BC T==1 on a spherical cap of a unit sphere and T==0 at infinity (approximated as r==(x^2 + y^2 + z^2)^0.5==40^0.5) and the flux over the remaining surfaces taken to be zero (only half domains has been specified due to symmetry reasons):

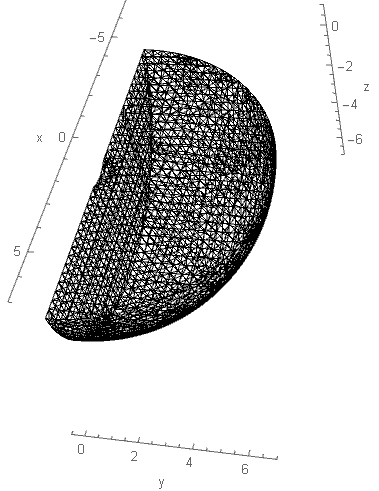
p = 0.2; Pe = 20; << NDSolve`FEM` boundaries = {-x^2 - y^2 - z^2 + 1, x^2 + y^2 + z^2 - 40, -y, z - p + 1}; \[CapitalOmega] = ToElementMesh[ ImplicitRegion[And @@ (# <= 0 & /@ boundaries), {x, y, z}]]; Show[\[CapitalOmega][ "Wireframe"["MeshElement" -> "MeshElements", Boxed -> True]], Axes -> True, AxesLabel -> {"x", "y", "z"}, PlotRange -> {{-7, 7}, {-0.5, 7}, {-7, 1}}] Show[\[CapitalOmega]["Wireframe"], Axes -> True, AxesLabel -> {"x", "y", "z"}, PlotRange -> {{-7, 7}, {-0.5, 7}, {-7, 1}}] 

The free-surface is located at z==-0.8 in the chosen reference system. The differential equation is:

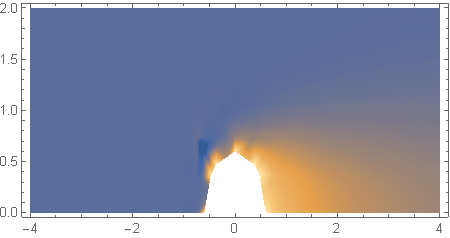
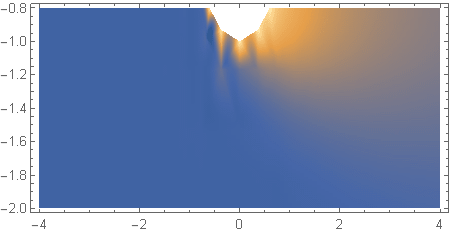
sol = NDSolveValue[{D[T[x, y, z], x] == 1/Pe Laplacian[T[x, y, z], {x, y, z}], {DirichletCondition[ T[x, y, z] == 1., boundaries[[1]] == 0.], DirichletCondition[T[x, y, z] == 0., boundaries[[2]] == 0.]}}, T, {x, y, z} \[Element] \[CapitalOmega]] 

I noticed a non-smooth behavior of the solution sol, as confirmed by the density plots:

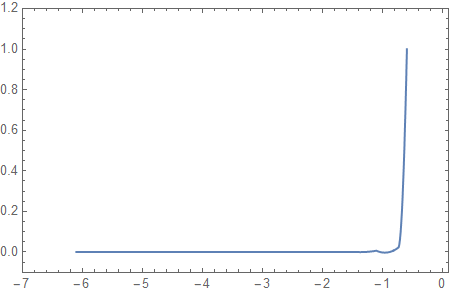
z1 = -0.8; DensityPlot[sol[x, y, z1], {x, -4, 4}, {y, 0, 2}, PlotRange -> All, PlotPoints -> 100, AspectRatio -> 1/2] DensityPlot[sol[x, 0, z], {x, -4, 4}, {z, -0.8, -2}, PlotRange -> All, PlotPoints -> 100, AspectRatio -> 1/2] 

and by some plots of the solution

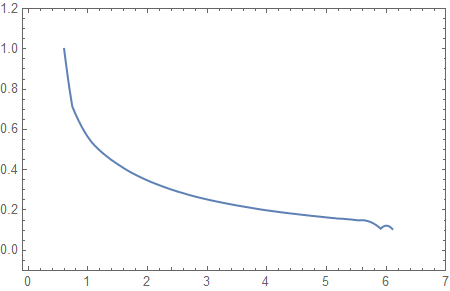
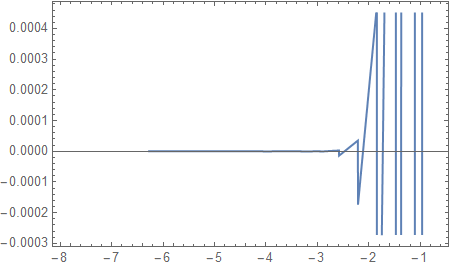
Plot[sol[x, 0, -0.8], {x, 0.6, 6.1}, Frame -> True, PlotRange -> {{-0.1, 7}, {-0.1, 1.2}}] Plot[sol[x, 0, -0.8], {x, -6.1, -0.6}, Frame -> True, PlotRange -> {{-7, 0.1}, {-0.1, 1.2}}] 

The derivatives of the solution show an even worse behavior. I report here as example just the derivative with respect to x:

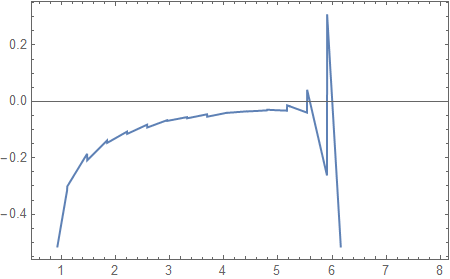
Dr[x_, y_, z_] = D[sol[x, y, z], x] Plot[Dr[x, 0, -0.8], {x, 0.6, 8}, Frame -> True] Plot[Dr[x, 0, -0.8], {x, -8, -0.6}, Frame -> True] 

I am interested in the derivative because I am trying to calculate the total flux of the gradient of sol through the two portion of the spherical cap, SC1 and SC2, which border the domain. As known, this is proportional to the heat flow through SC1 and SC2. The definition of SC1 and SC2 is:

SC1 = ImplicitRegion[ x^2 + y^2 + z^2 == 1 && z <= p - 1 && y >= 0 && x >= 0, {x, y, z}]; SC2 = ImplicitRegion[ x^2 + y^2 + z^2 == 1 && z <= p - 1 && y >= 0 && x <= 0, {x, y, z}]; Show[DiscretizeRegion[SC1, {{-5, 5}, {-5, 5}, {-3, 3}}, MaxCellMeasure -> 0.0001], Axes -> True, AxesLabel -> {"x", "y", "z"}, PlotRange -> {{-1, 1}, {-0.2, 1}, {-0.8, -1}}] Show[DiscretizeRegion[SC2, {{-5, 5}, {-5, 5}, {-3, 3}}, MaxCellMeasure -> 0.0001], Axes -> True, AxesLabel -> {"x", "y", "z"}, PlotRange -> {{-1, 1}, {-0.2, 1}, {-0.8, -1}}] 

and the heat flow through SC1 and SC2 should be:

NIntegrate[#, {x, y, z} \[Element] SC1] & /@ (Grad[ sol[x, y, z], {x, y, z}].{x, y, z}) NIntegrate[#, {x, y, z} \[Element] SC2] & /@ (Grad[ sol[x, y, z], {x, y, z}].{x, y, z}) 

Unfortunately, I get a lot of errors from the last calculation, I don't know if this happens because of the non-smooth behavior of the solution and of the derivative or for other mistakes that I am doing. Thank you in advance.