If you need derivatives of variables for later calculations, the best way is to solve for pure functions, where you get derivative very simply as shown. Second, with first order equations, you may not give derivative boundary conditions.(I gidn't check your solution)
sys = {s[1][t] + s[1][t]^2/40000 + 1/100 Derivative[1][s[1]][t] == 1/50 \[Tau][1][ t] (256000000/9 \[CurlyPhi][3][t] - 5120/9 (-9 \[Pi] Sin[64 \[Pi] t] + 15625 \[CurlyPhi][3][t]) - 64000000/9 \[CurlyPhi][4][t]), s[2][t] + s[2][t]^2/40000 + 1/100 Derivative[1][s[2]][t] == 1/50 \[Tau][2][ t] (64000000/9 \[CurlyPhi][3][t] - 2048/9 (-9 \[Pi] Sin[64 \[Pi] t] + 15625 \[CurlyPhi][3][t])), s[3][t] + s[3][t]^2/40000 + 1/100 Derivative[1][s[3]][t] == 1/50 \[Tau][3][ t] (-(128000000/9) \[CurlyPhi][3][t] + 1024/9 (-9 \[Pi] Sin[64 \[Pi] t] + 15625 \[CurlyPhi][3][t]) + 64000000/9 \[CurlyPhi][4][t]), s[4][t] + s[4][t]^2/40000 + 1/100 Derivative[1][s[4]][t] == 1/50 \[Tau][4][ t] (64000000/9 \[CurlyPhi][3][t] - 128000000/9 \[CurlyPhi][4][t] + 64000000/9 \[CurlyPhi][5][t]), s[5][t] + s[5][t]^2/40000 + 1/100 Derivative[1][s[5]][t] == 1/50 \[Tau][5][ t] (64000000/9 \[CurlyPhi][4][t] - 128000000/9 \[CurlyPhi][5][t] + 64000000/9 \[CurlyPhi][6][t]), s[6][t] + s[6][t]^2/40000 + 1/100 Derivative[1][s[6]][t] == 1/50 \[Tau][6][ t] (64000000/9 \[CurlyPhi][5][t] - 128000000/9 \[CurlyPhi][6][t] + 64000000/9 \[CurlyPhi][7][t]), s[7][t] + s[7][t]^2/40000 + 1/100 Derivative[1][s[7]][t] == 1/50 \[Tau][7][ t] (64000000/9 \[CurlyPhi][6][t] + 64000000/ 9 ((4131 \[Pi] Sin[64 \[Pi] t])/734375 + 1/4 \[CurlyPhi][7][t]) - 128000000/9 \[CurlyPhi][7][t]), s[8][t] + s[8][t]^2/40000 + 1/100 Derivative[1][s[8]][t] == 1/50 \[Tau][8][ t] (2506752/47 \[Pi] Sin[64 \[Pi] t] - 128000000/ 9 ((4131 \[Pi] Sin[64 \[Pi] t])/734375 + 1/4 \[CurlyPhi][7][t]) + 64000000/9 \[CurlyPhi][7][t]), s[9][t] + s[9][t]^2/40000 + 1/100 Derivative[1][s[9]][t] == 1/50 \[Tau][9][ t] (5013504/47 \[Pi] Sin[64 \[Pi] t] - 64000000/9 \[CurlyPhi][6][t] - 320000000/ 9 ((4131 \[Pi] Sin[64 \[Pi] t])/734375 + 1/4 \[CurlyPhi][7][t]) + 256000000/9 \[CurlyPhi][7][t]), \[Tau][1][ t] + (s[1][t] \[Tau][1][t])/40000 + 1/100 Derivative[1][\[Tau][1]][t] == 100 (256000000/9 \[CurlyPhi][3][t] - 5120/9 (-9 \[Pi] Sin[64 \[Pi] t] + 15625 \[CurlyPhi][3][t]) - 64000000/9 \[CurlyPhi][4][t]), \[Tau][2][ t] + (s[2][t] \[Tau][2][t])/40000 + 1/100 Derivative[1][\[Tau][2]][t] == 100 (64000000/9 \[CurlyPhi][3][t] - 2048/9 (-9 \[Pi] Sin[64 \[Pi] t] + 15625 \[CurlyPhi][3][t])), \[Tau][3][ t] + (s[3][t] \[Tau][3][t])/40000 + 1/100 Derivative[1][\[Tau][3]][t] == 100 (-(128000000/9) \[CurlyPhi][3][t] + 1024/9 (-9 \[Pi] Sin[64 \[Pi] t] + 15625 \[CurlyPhi][3][t]) + 64000000/9 \[CurlyPhi][4][t]), \[Tau][4][ t] + (s[4][t] \[Tau][4][t])/40000 + 1/100 Derivative[1][\[Tau][4]][t] == 100 (64000000/9 \[CurlyPhi][3][t] - 128000000/9 \[CurlyPhi][4][t] + 64000000/9 \[CurlyPhi][5][t]), \[Tau][5][ t] + (s[5][t] \[Tau][5][t])/40000 + 1/100 Derivative[1][\[Tau][5]][t] == 100 (64000000/9 \[CurlyPhi][4][t] - 128000000/9 \[CurlyPhi][5][t] + 64000000/9 \[CurlyPhi][6][t]), \[Tau][6][ t] + (s[6][t] \[Tau][6][t])/40000 + 1/100 Derivative[1][\[Tau][6]][t] == 100 (64000000/9 \[CurlyPhi][5][t] - 128000000/9 \[CurlyPhi][6][t] + 64000000/9 \[CurlyPhi][7][t]), \[Tau][7][ t] + (s[7][t] \[Tau][7][t])/40000 + 1/100 Derivative[1][\[Tau][7]][t] == 100 (64000000/9 \[CurlyPhi][6][t] + 64000000/ 9 ((4131 \[Pi] Sin[64 \[Pi] t])/734375 + 1/4 \[CurlyPhi][7][t]) - 128000000/9 \[CurlyPhi][7][t]), \[Tau][8][ t] + (s[8][t] \[Tau][8][t])/40000 + 1/100 Derivative[1][\[Tau][8]][t] == 100 (2506752/47 \[Pi] Sin[64 \[Pi] t] - 128000000/ 9 ((4131 \[Pi] Sin[64 \[Pi] t])/734375 + 1/4 \[CurlyPhi][7][t]) + 64000000/9 \[CurlyPhi][7][t]), \[Tau][9][ t] + (s[9][t] \[Tau][9][t])/40000 + 1/100 Derivative[1][\[Tau][9]][t] == 100 (5013504/47 \[Pi] Sin[64 \[Pi] t] - 64000000/9 \[CurlyPhi][6][t] - 320000000/ 9 ((4131 \[Pi] Sin[64 \[Pi] t])/734375 + 1/4 \[CurlyPhi][7][t]) + 256000000/9 \[CurlyPhi][7][t]), 128000000/9 Derivative[1][\[CurlyPhi][3]][t] - 1024/9 (-576 \[Pi]^2 Cos[64 \[Pi] t] + 15625 Derivative[1][\[CurlyPhi][3]][t]) - 64000000/9 Derivative[1][\[CurlyPhi][4]][ t] == (-(64000000/9) \[Tau][2][t] + 128000000/9 \[Tau][3][t] - 64000000/9 \[Tau][4][t])/ 1000, -(64000000/9) Derivative[1][\[CurlyPhi][3]][t] + 128000000/9 Derivative[1][\[CurlyPhi][4]][t] - 64000000/9 Derivative[1][\[CurlyPhi][5]][ t] == (-(64000000/9) \[Tau][3][t] + 128000000/9 \[Tau][4][t] - 64000000/9 \[Tau][5][t])/ 1000, -(64000000/9) Derivative[1][\[CurlyPhi][4]][t] + 128000000/9 Derivative[1][\[CurlyPhi][5]][t] - 64000000/9 Derivative[1][\[CurlyPhi][6]][ t] == (-(64000000/9) \[Tau][4][t] + 128000000/9 \[Tau][5][t] - 64000000/9 \[Tau][6][t])/ 1000, -(64000000/9) Derivative[1][\[CurlyPhi][5]][t] + 128000000/9 Derivative[1][\[CurlyPhi][6]][t] - 64000000/9 Derivative[1][\[CurlyPhi][7]][ t] == (-(64000000/9) \[Tau][5][t] + 128000000/9 \[Tau][6][t] - 64000000/9 \[Tau][7][t])/ 1000, -(64000000/9) Derivative[1][\[CurlyPhi][6]][t] - 64000000/ 9 ((264384 \[Pi]^2 Cos[64 \[Pi] t])/734375 + 1/4 Derivative[1][\[CurlyPhi][7]][t]) + 128000000/9 Derivative[1][\[CurlyPhi][7]][ t] == (-(64000000/9) \[Tau][6][t] + 128000000/9 \[Tau][7][t] - 64000000/9 \[Tau][8][t])/1000, s[1][0] == 0, s[2][0] == 0, s[3][0] == 0, s[4][0] == 0, s[5][0] == 0, s[6][0] == 0, s[7][0] == 0, s[8][0] == 0, s[9][0] == 0, \[Tau][1][0] == 0, \[Tau][2][0] == 0, \[Tau][3][0] == 0, \[Tau][4][0] == 0, \[Tau][5][0] == 0, \[Tau][6][0] == 0, \[Tau][7][0] == 0, \[Tau][8][0] == 0, \[Tau][9][0] == 0, \[CurlyPhi][3][0] == 0, \[CurlyPhi][4][0] == 0, \[CurlyPhi][5][0] == 0, \[CurlyPhi][6][0] == 0, \[CurlyPhi][7][0] == 0};
.
var = {\[CurlyPhi][3][t], \[CurlyPhi][4][t], \[CurlyPhi][5][ t], \[CurlyPhi][6][t], \[CurlyPhi][7][t], s[1][t], s[2][t], s[3][t], s[4][t], s[5][t], s[6][t], s[7][t], s[8][t], s[9][t], \[Tau][1][t], \[Tau][2][t], \[Tau][3][t], \[Tau][4][ t], \[Tau][5][t], \[Tau][6][t], \[Tau][7][t], \[Tau][8][ t], \[Tau][9][t]} /. aa_[t] -> aa ({U, S} = {{-(96/125) \[Pi] Sin[64 \[Pi] t], 4000/3 \[CurlyPhi][3][t], 8/375 (9 \[Pi] Sin[64 \[Pi] t] - 15625 \[CurlyPhi][3][t] + 62500 \[CurlyPhi][4][t]), -(4000/3) (\[CurlyPhi][3][ t] - \[CurlyPhi][5][t]), -(4000/3) (\[CurlyPhi][4][ t] - \[CurlyPhi][6][t]), -(4000/3) (\[CurlyPhi][5][ t] - \[CurlyPhi][7][t]), (44064 \[Pi] Sin[64 \[Pi] t])/ 5875 - 4000/3 \[CurlyPhi][6][t] + 1000/3 \[CurlyPhi][7][t], (58752 \[Pi] Sin[64 \[Pi] t])/5875 - 4000/3 \[CurlyPhi][7][t], 0}, {-4000 \[Tau][1][t] + 16000/3 \[Tau][2][t] - 4000/3 \[Tau][3][t], -(4000/3) \[Tau][1][t] + 4000/3 \[Tau][3][t], -(4000/3) \[Tau][2][t] + 4000/3 \[Tau][4][t], -(4000/3) \[Tau][3][t] + 4000/3 \[Tau][5][t], -(4000/3) \[Tau][4][t] + 4000/3 \[Tau][6][t], -(4000/3) \[Tau][5][t] + 4000/3 \[Tau][7][t], -(4000/3) \[Tau][6][t] + 4000/3 \[Tau][8][t], -(4000/3) \[Tau][7][t] + 4000/3 \[Tau][9][t], 4000/3 \[Tau][7][t] - 16000/3 \[Tau][8][t] + 4000 \[Tau][9][t]}}); T = 0.03125 // Rationalize[#, 0] &; varsol = NDSolve[sys, var, {t, 0, 6 T}] // Flatten;
.
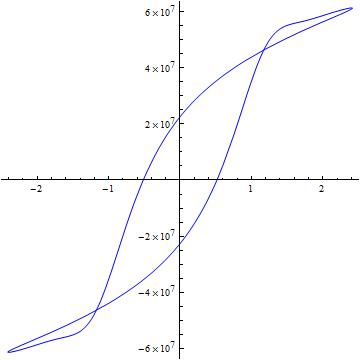
vp[t_] = -(96/125) \[Pi] Sin[64 \[Pi] t]; ParametricPlot[ Evaluate[{vp[t], (-1000 D[U, t] + S)[[5]] /. varsol}], {t, 5 T, 6 T}, PlotStyle -> {Blue}, PlotRange -> Full, AspectRatio -> 1]