EDIT: Approximations for large and small z
For large z
int3[n_Integer?NonNegative, z_?Positive] = Evaluate@ Assuming[Element[n, NonNegativeIntegers], Asymptotic[(2*Gamma[5/2 + n]*MeijerG[{{}, {2 + n}}, {{-(1/2), 1, 3/2}, {}}, z^2/4])/ (Sqrt[Pi]*BesselK[2, z]), {z, Infinity, 3}] // FullSimplify] (* (1/Sqrt[π])2^(-2 + n) z^(-3 - n) (-3 (1 + n) (130 + n (410 + n (402 + n (178 + n (37 + 3 n))))) + 2 (1 + n) (55 + n (109 + n (55 + 9 n))) z - 8 (1 + n) (5 + 3 n) z^2 + 16 z^3) Gamma[5/2 + n] *) Comparing with int1
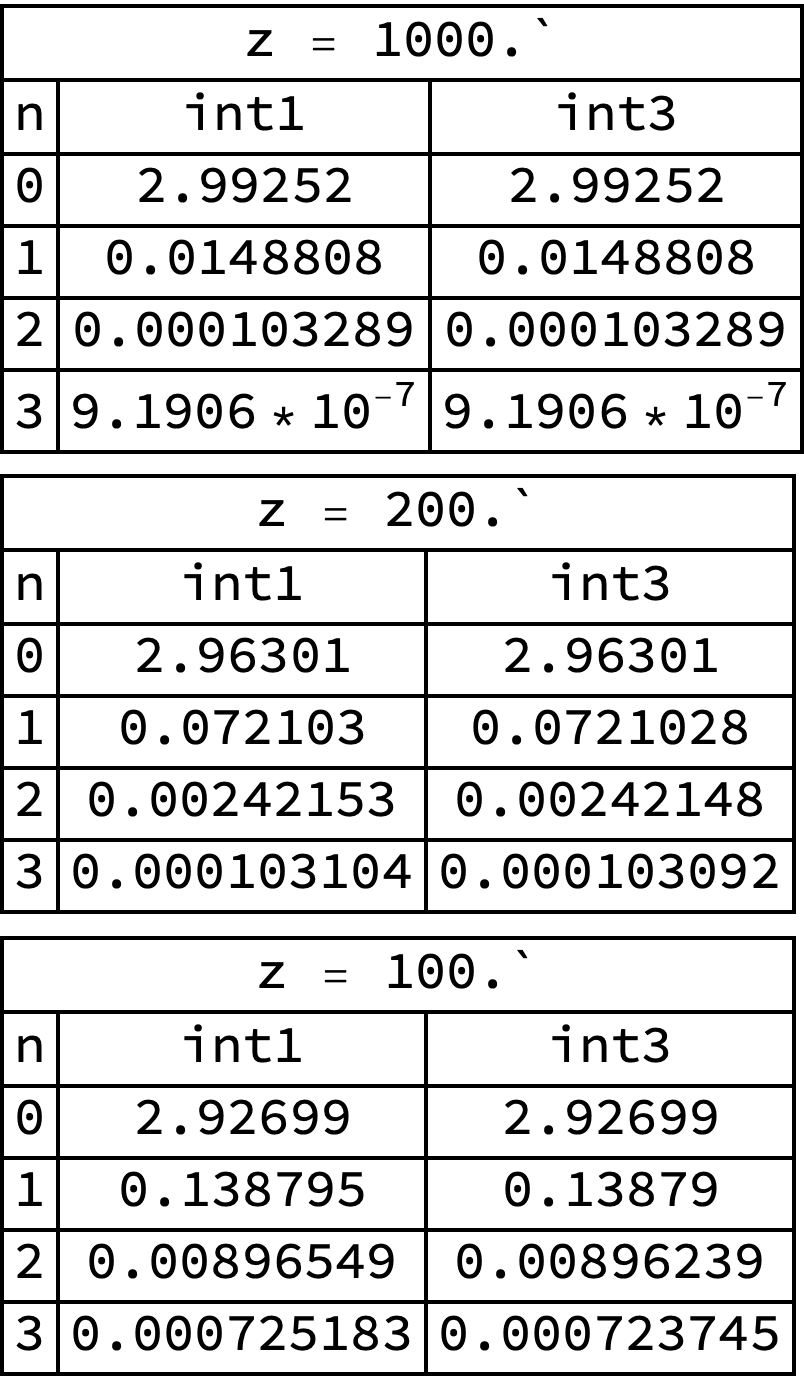
Table[ Grid[ Join[ {{StringForm["z = ``", z], SpanFromLeft}, {n, int1, int3}}, Table[ {n, int1[n][SetPrecision[z, 900]], int3[n, z]}, {n, 0, 3}]] /. x_Real :> N[x], Frame -> All], {z, {1000., 200., 100.}}] // Column For small z
int4[n_Integer?NonNegative, z_?Positive] = Evaluate@ Assuming[Element[n, NonNegativeIntegers] && z > 0, Asymptotic[(2*Gamma[5/2 + n]*MeijerG[{{}, {2 + n}}, {{-(1/2), 1, 3/2}, {}}, z^2/4])/ (Sqrt[Pi]*BesselK[2, z]), {z, 0, 5}] // FullSimplify] (* (Sqrt[π] z^4 Gamma[5/2 + n])/(3 n!) + 1/32 z (32 - 16 (1 + n) z^2 + 2 (-8 + 4 EulerGamma (1 + n)^2 - n (16 + 7 n)) z^4 + z^4 ((3 + 4 n (2 + n)) HarmonicNumber[-(1/2) + n] + 8 n (2 + n) Log[z] + Log[z^8/4])) *) Comparing with int1
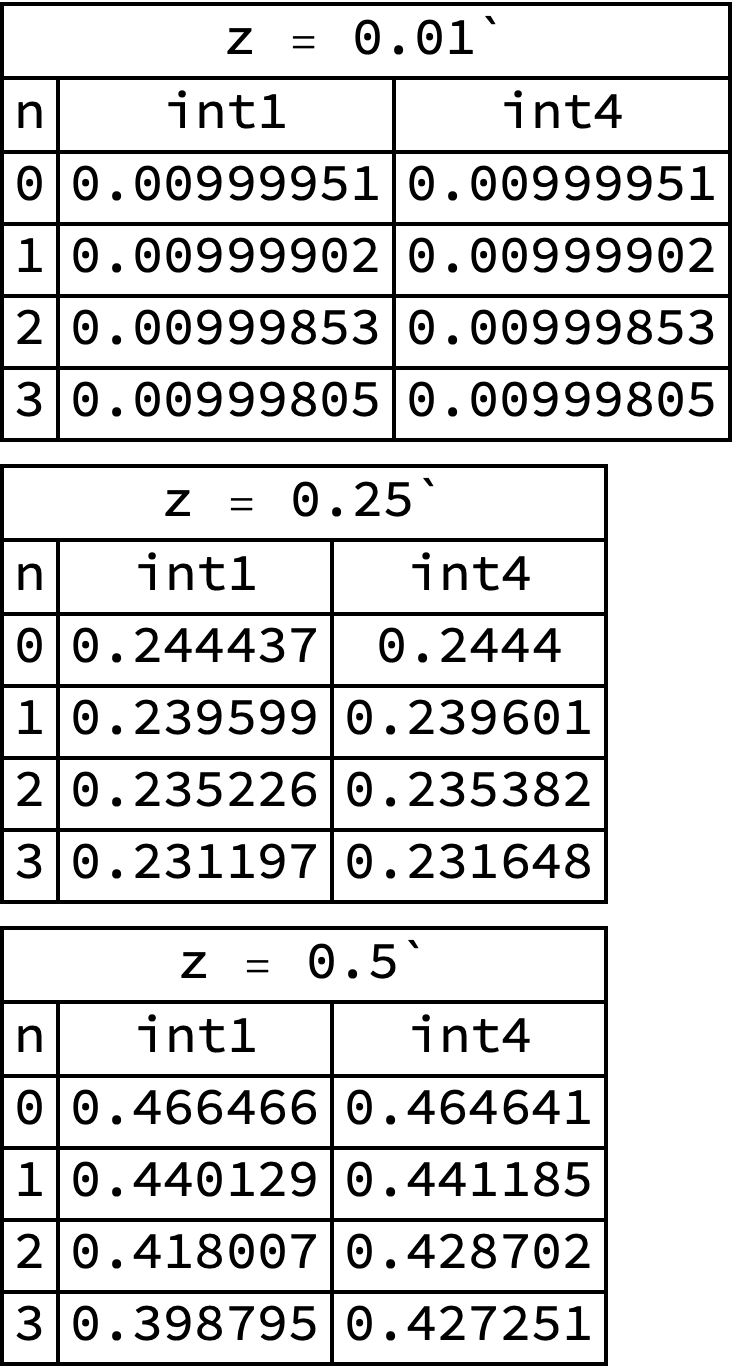
Table[ Grid[ Join[ {{StringForm["z = ``", z], SpanFromLeft}, {n, int1, int4}}, Table[{n, int1[n][z], int4[n, z]}, {n, 0, 3}]], Frame -> All], {z, {0.01, 0.25, 0.5}}] // Column