I propose "deintersection" algorithm.
Let we have $n$ random points.
n = 10; p = RandomReal[1.0, {n, 2}]; We want change the order of this points to get rid of the intersections.
Line segments $(p_1,p_2)$ and $(p_3,p_4)$ intersect if and only if the signs of areas of triangles $p_1p_2p_3$ and $p_1p_2p_4$ are different and the signs of areas of triangles $p_3p_4p_1$ and $p_3p_4p_1$ are also different.
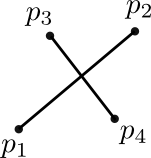
Corresponding function
SignedArea[p1_, p2_, p3_] := 0.5 (#1[[2]] #2[[1]] - #1[[1]] #2[[2]]) &[p2 - p1, p3 - p1]; IntersectionQ[p1_, p2_, p3_, p4_] := SignedArea[p1, p2, p3] SignedArea[p1, p2, p4] < 0 && SignedArea[p3, p4, p1] SignedArea[p3, p4, p2] < 0; Main step
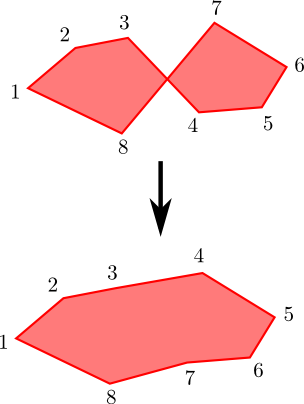
Patterns in Mathematica are very convenient for the searching and removing intersections.
Deintersect[p_] := Append[p, p[[1]]] //. {s1___, p1_, p2_, s2___, p3_, p4_, s3___} /; IntersectionQ[p1, p2, p3, p4] :> ({s1, p1, p3, Sequence @@ Reverse@{s2}, p2, p4, s3}) // Most; To add the segment between the last and the first point I use Append and Most.
As a result we got the polygon without intersections
p2 = Deintersect[p]; Graphics[{Lighter@Red, EdgeForm@Thickness[0.01], EdgeForm@Red, Polygon[p2]}] 
And many other funny polygons
Graphics[{Lighter@Red, EdgeForm@Thickness[0.01], EdgeForm@Red, Polygon[#]}, ImageSize -> 100] &@Deintersect[#] & /@ RandomReal[1.0, {10, n, 2}] 
As you can see, this algorithm can give more complicated polygons than in other answers.
