From Is there any way to reveal a removable singularity in a plot?Is there any way to reveal a removable singularity in a plot?:
Here is an update. It is I hope written in a somewhat better style. I also took the opportunity to add a couple of features. PlotPiecewise will automatically apply Piecewise expandPiecewiseExpand, and if it produces a Piecewise function it will plot it. It will also handle a wider range of conditions in a Piecewise function. There is a bit more error checking, and some error messages have been added. It is still not HoldAll. Since Mr.Wizard prodded me to improve the code, I tried to keep it so that it would work in V7.
Here is an update. It is I hope written in a somewhat better style. I also took the opportunity to add a couple of features. PlotPiecewise will automatically apply Piecewise expand, and if it produces a Piecewise function it will plot it. It will also handle a wider range of conditions in a Piecewise function. There is a bit more error checking, and some error messages have been added. It is still not HoldAll. Since Mr.Wizard prodded me to improve the code, I tried to keep it so that it would work in V7.
Here is an update. It is I hope written in a somewhat better style. I also took the opportunity to add a couple of features. PlotPiecewise will automatically apply PiecewiseExpand, and if it produces a Piecewise function it will plot it. It will also handle a wider range of conditions in a Piecewise function. There is a bit more error checking, and some error messages have been added. It is still not HoldAll. Since Mr.Wizard prodded me to improve the code, I tried to keep it so that it would work in V7.
Update 2015-7-13: PlotPiecewise now handles discontinuities of non-Piecewise functions. (It basically did this before, but required the head to be Piecewise or contain a built-in discontinuous function, like Sign. All I did was brainlessly wrap a function in Piecewise. I also had to rewrite some of the Reduce/PiecewiseExpand code. One of the more complicated examples, which used to expand to a number of integer cases, kept the integer parameter instead of expanding; in another (not shown), the Ceiling of a complicated function was no longer expanded into a Piecewise function.
Update: PlotPiecewise now automatically tries to convert a non-Piecewise function into one using PiecewiseExpand. PiecewiseExpand will also do some simplification, such as factoring and reducing a rational function; to avoid that, pass a Piecewise function directly. PlotPiecewise will not alter the formulas in a Piecewise. Note, however, that Mathematica automatically reduces x (x - 1) / (x (x - 2)) but not (x^2 - x) / (x (x - 2)).
New examples (2015-7-13)
From Is there any way to reveal a removable singularity in a plot?:
PlotPiecewise[(2^x - 2)/(x - 1), {x, -2, 2}, "DotSize" -> Offset[{3, 3}], "EmptyDotStyle" -> EdgeForm[Directive[ColorData[97, 1], AbsoluteThickness[1.6]]]] 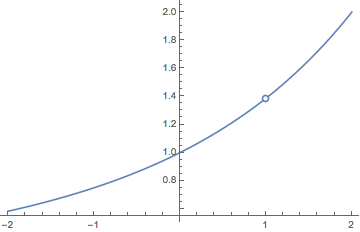
A similar one:
PlotPiecewise[(2^x - 2)/(x^2 - 1), {x, -2, 2}] 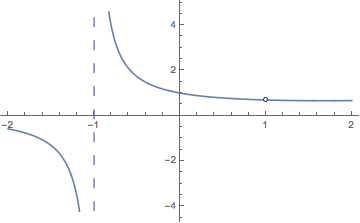
Clear[ PlotPiecewiseClearAll[PlotPiecewise, (* user interface *) PlotPiecewise`plot, (* generates the plot of a `Piecewise` function *) PlotPiecewiseDotPlotPiecewise`init, (* handles the end points of subdomains -- Sows empty/filled dots and asymptotes *) InteriorPoints, (* handles discontinuities in the interior of a subdomain *) PlotPiecewise`solve, (* Reduce + postprocessingPlotPiecewise`expand, to handle more general PiecewisePlotPiecewise`annotatedPoints, conditionsPlotPiecewise`boundaryPoints, *) PlotPiecewise`expand]; (* Used by PlotPiecewise`solve toPlotPiecewise`interiorPoints, expandPlotPiecewise`sowAnnotations, generated parameter C[1] *)PlotPiecewise`inDomain]; PlotPiecewise::usage = "PlotPiecewise[Piecewise[...], {x, a, b}, opts]"; PlotPiecewise::limindet = "Limit `` is not numeric or infinite at ``"; PlotPiecewise::nonpw = "Function `` is not a Piecewise function or did not expand to one"; PlotPiecewise`debug::debug = "``"; PlotPiecewise`debug::plot = "``"; PlotPiecewise`debug::annotation = "``"; PlotPiecewise`debug::limit = "``"; PlotPiecewise`debug = Hold[PlotPiecewise`debug::debug, PlotPiecewise`debug::plot, PlotPiecewise`debug::annotation, PlotPiecewise`debug::limit]; Off @@ PlotPiecewise`debug; Options[PlotPiecewise] = Join[{"DotSize" -> Automatic, "EmptyDotStyle" -> Automatic, "FilledDotStyle" -> Automatic, "AsymptoteStyle" -> Automatic, "BaseDotSize" -> Offset[{2, 2}], "AdditionalPoints" -> {}, (* addition pts to annotate *) "PiecewiseExpand" -> Automatic, (* which fns. to expand *) "ContinuousEndpoints" -> Automatic},(* eval. formula, not limit *) Options[Plot]]; Options[EmptyDot] = Options[FilledDot] = Options[Asymptote] = Options[PlotPiecewise`plot] = Options[PlotPiecewise`init] = Options[PlotPiecewise]; (* graphics elements *) Clear[EmptyDot, FilledDot, Asymptote]; EmptyDot[pt_, opts : OptionsPattern[]] /; OptionValue["EmptyDotStyle"] === None := {}; FilledDot[pt_, opts : OptionsPattern[]] /; OptionValue["FilledDotStyle"] === None := {}; Asymptote[pt_, opts : OptionsPattern[]] /; OptionValue["AsymptoteStyle"] === None := {}; EmptyDot[pt_, opts : OptionsPattern[]] := {White, OptionValue["EmptyDotStyle"] /. Automatic -> {}, Disk[pt, OptionValue["DotSize"] /. Automatic -> OptionValue["BaseDotSize"]]}; FilledDot[pt_, opts : OptionsPattern[]] := {OptionValue["FilledDotStyle"] /. Automatic -> {}, Disk[pt, OptionValue["DotSize"] /. Automatic -> OptionValue["BaseDotSize"]]}; Asymptote[x0_, opts : OptionsPattern[]] := {Dashing[Large], OptionValue["AsymptoteStyle"] /. Automatic -> {}, Line[Thread[{x0, OptionValue[PlotRange][[2]]}]]}; (* PlotPieceDot - Sows piecewise breaks, tagged with three ids; "filled" -> {x,y}; "empty" -> {x,y}; "asymptote" -> x; An entry in a Piecewise function has the form: piece = {formula, condition} *) PlotPiecewise`$inequality = Greater | Less | LessEqual | GreaterEqual; PlotPiecewise`$discontinuousAuto = Ceiling | Floor | Round | Sign; PlotPiecewise`$discontinuousAll = Ceiling | Floor | Round | Sign |(**Min|Max|Clip|*)UnitStep some| constants * IntegerPart |(*FractionalPart|*)Mod | Quotient | UnitBox | $filledRelations = Equal | LessEqual | GreaterEqual; $emptyRelations = Greater UnitTriangle | Less; $inequality SquareWave(*|TriangleWave|SawtoothWave*)(*|BernsteinBasis|\ BSplineBasis|Abs|If|Which|Switch*); PlotPiecewise`$discontinuous = GreaterCeiling | LessFloor | LessEqualRound | GreaterEqual;Sign; (* auxiliary function:functions*) (* causes Conditional solutions to expand to all possibilities; (arises from trig eq, and C[1] -- perhaps C[2], etc? *) PlotPiecewise`expand[cond_Or, var_] := PlotPiecewise`expand[#, var] & /@ cond; PlotPiecewise`expand[cond_, var_] := Reduce[cond, var, Backsubstitution -> True]; PlotPiecewise`solve[eq_, var_] /; MemberQ[eq, PlotPiecewise`$discontinuous, Infinity, Heads -> True] := PlotPiecewise`solve[# == C[1] && C[1] ∈ Integers && And @@ Cases[eq, Except[_Equal]], var] & /@ Cases[eq, PlotPiecewise`$discontinuous[e_] :> e, Infinity]; PlotPiecewise`solve[eq_, var_] := {var -> (var /. #)} & /@ List @ ToRules @List@ToRules@ PlotPiecewise`expand[ Reduce[eq, var, Reals, Backsubstitution -> True], var] /. {False -> {}}; (* PlotPiecewiseDotlimit routines for handling discontinuous functions, which Limit fails to do *) Needs["NumericalCalculus`"]; PlotPiecewise`nlimit[f_?NumericQ, var_ -> x0_, dir_] := f; PlotPiecewise`nlimit[f_, var_ -> x0_, dir_] := NLimit[f, var -> x0, dir]; PlotPiecewise`limit[f_, var_ Calls-> auxiliaryx0_, functiondir_] InteriorPoints/; MemberQ[Numerator[f], PlotPiecewise`$discontinuous, BreaksInfinity, down compound inequalities into simpleHeads inequalities-> True] := Module[{y0, f0}, From simplef0 inequalities= f //. (disc : PlotPiecewise`$discontinuous)[z_] /; FreeQ[z, PlotPiecewise`$discontinuous] :> disc[ With[{dz = Abs[D[z, determinesvar] dots/asymptotes. var -> N@x0]}, From equalities Mean[{z /. var -> N@x0, sows a dot z /. var -> x0 - 0.1 Last[dir]/Max[1, ifdz]}]] formula ]; Message[PlotPiecewise`debug::limit, {f0, f, var -> x0, dir}]; Quiet[Check[y0 = PlotPiecewise`nlimit[f0, var -> x0, dir], Check[y0 = Limit[f0, var -> x0, dir], If[! NumericQ[y0], y0 = Indeterminate]]], {Power::infy, Infinity::indet, NLimit::noise}]; y0 ]; PlotPiecewise`limit[f_, var_ -> x0_, dir_] := Module[{y0}, Quiet[Check[y0 = f /. var -> x0, Check[y0 = Limit[f, var -> x0, dir], If[! NumericQ[y0], y0 = Indeterminate]]], {Power::infy, Infinity::indet}]; y0 ]; PlotPiecewise`$reverseIneq = {Less -> Greater, Greater -> Less, LessEqual -> GreaterEqual}; PlotPiecewise`reverseIneq[(rel : PlotPiecewise`$inequality)[ args__]] := (rel /. PlotPiecewise`$reverseIneq) @@ Reverse@{args}; PlotPiecewise`inDomain[] := LessEqual @@ PlotPiecewise`domain[[{2, 1, 3}]]; PlotPiecewise`inDomain[dom_] := LessEqual @@ dom[[{2, 1, 3}]]; (* annotatedPoints -- returns list of abscissas to be "annotated" with dots/asymptotes boundaryPoints -- returns list of boundaries numbers between \ pieces interiorPoints -- returns list of points where the \ denominator is definedzero *) PlotPiecewiseDot[piece_] := (InteriorPoints[piece]; PlotPiecewiseDot[piece, "sow"]); PlotPiecewiseDot[{formula_, HoldPattern @ Inequality[a_, rel1_, b_PlotPiecewise`annotatedPoints[allpieces_, rel2_domain_, c_]}, "sow"]additionalpoints_] := PlotPiecewiseDot[#,DeleteDuplicates@Flatten@Join[ "sow"] & /@ {{formula, rel1[a, b]}, {formulaPlotPiecewise`boundaryPoints[allpieces, rel2[bdomain], c]}}; PlotPiecewiseDot[{formula_, (rel : $inequality)[a_, b_, c_]}PlotPiecewise`interiorPoints[allpieces, "sow"] :=domain], PlotPiecewiseDot[#, "sow"] & /@ {{formula,additionalpoints rel[a, b]}, {formula, rel[b, c]}};]; PlotPiecewiseDot[PlotPiecewise`boundaryPoints[allpieces_, domain : {formula_var_, cond_Equal}_, "sow"]_}] := With[{aconditions = PlotPiecewise`var DeleteDuplicates[ Equal @@@ Flatten[Last /.@ #, yy = formula allpieces /. #} {HoldPattern@ Inequality[a_, rel1_, b_, rel2_, If[NumericQ[Abs[yy]] c_] :> {PlotPiecewise`reverseIneq[rel1[a, b]], Sow[ rel2[b, c]}, (rel : PlotPiecewise`$inequality)[a_, b_, c_] :> {aPlotPiecewise`reverseIneq[rel[a, yyb]], rel[b, c]}} ]]}, "filled"]]] Message[PlotPiecewise`debug::annotation, conditions]; var /. Flatten[ (* deletes no soln {}'s *) PlotPiecewise`solve[# && PlotPiecewise`inDomain[domain], var] & /@ conditions, 1] /. var -> {} (* no BPs in domain *) ]; PlotPiecewise`interiorPoints[allpieces_, domain : {var_, _, _}] := MapThread[ Function[{formula, condition}, Flatten[ {With[{solns = PlotPiecewise`solve[ cond Denominator[formula, Trig -> True] == 0 && (condition /. {LessEqual -> Less, GreaterEqual -> Greater}) && LessEqual @@ PlotPiecewise`domain[[{2, 1, 3}]], PlotPiecewise`var] (* check =? *); PlotPiecewise`var]}, PlotPiecewiseDot[ PlotPiecewise`var /. solns /. PlotPiecewise`var -> {formula_,} cond : (rel : $inequality)[_, _]}, "sow"] := With[{a = PlotPiecewise`var /. #, yy = Limit[formula, First @ #, Direction -> If[MatchQ[rel, Greater | GreaterEqual], 1, -1]]}, If[Abs[yy] == Infinity, Sow[a, "asymptotes"], If[NumericQ[yy], Sow[{a, yy}, If[MatchQ[rel, $filledRelations] ], "filled" If[MemberQ[Numerator[formula], "empty"]]PlotPiecewise`$discontinuous, Message[PlotPiecewise::limindet, yyInfinity, a]]Heads -> True], ]] &With[{solns /@= PlotPiecewise`solve[ Equal @@ cond Numerator[formula] == 0 && (condition /. {LessEqual -> Less, GreaterEqual -> Greater}) && LessEqual @@ PlotPiecewise`domain[[{2, 1, 3}]], PlotPiecewise`var]}, PlotPiecewise`var /. solns /. PlotPiecewise`var -> {} ], {} ]} ]], Transpose@allpieces ]; (* checksowAnnotations =?- *)Sows irregular points, tagged with three ids; "filled" \[Rule] {x,y}; (* "empty" \[Rule] {x,y}; auxiliary function: finds discontinuities"asymptote" inside\[Rule] intervals x; *) InteriorPoints[PlotPiecewise`sowAnnotations[allpieces_, domain : {formula_var_, cond_a_, b_}, {}] := {}; PlotPiecewise`sowAnnotations[allpieces_, domain With[: {solnsvar_, a_, b_}, points_List] := (Message[PlotPiecewise`debug::annotation, "sowAnn" PlotPiecewise`solve[-> {allpieces, points}]; PlotPiecewise`sowAnnotations[allpieces, domain, ##] & Denominator[formula@@@ Partition[{If[First[#] == a, TrigIndeterminate, a]}~Join~#~ Join~{If[Last[#] == b, Indeterminate, b]}, 3, 1] &@ SortBy[points, N]); PlotPiecewise`sowAnnotations[allpieces_, domain : {var_, _, _}, xminus_, x0_?NumericQ, xplus_] := Module[{y0, yplus, yminus, f0, fminus, fplus}, f0 = First[ Pick @@ MapAt[# /. var -> True]x0 ==& 0/@ &&# &, Transpose@allpieces, (cond2] /. {LessEqual} -> Less,{Indeterminate}]; GreaterEqual Quiet[y0 = f0 /. var -> GreaterN@x0, {Power::infy, Infinity::indet})]; && If[xminus =!= Indeterminate, (* xminus ≠ left endpoint *) fminus = LessEqual First[Pick @@ PlotPiecewise`domain[[ MapAt[# /. var -> Mean[{2xminus, 1x0}] & /@ # &, 3 Transpose@allpieces, 2] /. {}]] -> {Indeterminate}]; yminus = PlotPiecewise`limit[fminus, var -> x0, Direction -> 1]; ]; If[xplus PlotPiecewise`var]}=!= Indeterminate, (* xplus ≠ right endpoint *) With[{a fplus = PlotPiecewise`varFirst[ Pick @@ MapAt[# /. var -> Mean[{x0, xplus}] & /@ # &, yy = Limit[formula Transpose@allpieces, First@#]2] /. {}, -> {Indeterminate}]; yplus = PlotPiecewise`limit[fplus, If[Abs[yy]var ==-> Infinityx0, Direction -> -1]; ]; If[Abs[yminus] == Sow[a,Infinity "asymptotes"]|| Abs[yplus] == Infinity, Sow[x0, "asymptote"]]; If[NumericQ[yy] If[NumericQ[y0], Sow[{ax0, yyy0}, "empty"],"filled"]]; Message[ Message[PlotPiecewisePlotPiecewise`debug::limindetannotation, yy{{x0, a]]y0, f0}, {xminus, yminus, fminus}, ]]{xplus, yplus, fplus}}]; Sow[{x0, #}, "empty"] & /@ solns DeleteDuplicates@DeleteCases[Select[{yminus, yplus}, NumericQ], y0] ]; (* initialization of context variables *) PlotPiecewise`init[f : HoldPattern@Piecewise[pieces_, default_], domain : {var_, _, _}, opts : OptionsPattern[]] := (PlotPiecewise`domain = SetPrecision[domain, Infinity]; PlotPiecewise`var = var; PlotPiecewise`allpieces = If[default =!= Indeterminate, Append[pieces,(* add True case to pieces *) {default, If[Head[#] === Not, Reduce[#], #] &@ Simplify[Not[Or @@ (Last /@ pieces)]]}], pieces] /. {formula_, HoldPattern@Or[e__]} :> Sequence @@ ({formula, #} & /@ List[e]); PlotPiecewise`$discontinuous = OptionValue[ "PiecewiseExpand"] /. {Automatic -> PlotPiecewise`$discontinuousAuto, All -> PlotPiecewise`$discontinuousAll, None -> {}}; Message[PlotPiecewise`debug::debug, "f" -> f] ); (* The main plotting function *) PlotPiecewise`plot[f : HoldPattern @ Piecewise[pieces_, default_], domain : {var_, a_, b_}, opts : OptionsPattern[]] /; (PlotPiecewise`var = var; PlotPiecewise`domain = SetPrecision[domain, Infinity]; True) := With[{exceptions = Last @ Reap[ PlotPiecewiseDot[#(*,opts*)] & /@ If[default =!= Indeterminate, Append[pieces, (* add True (default) case to pieces *) {default, Reduce[Not[Or @@ (Last /@ pieces)]]}], pieces], {"asymptotes", "empty", "filled"}], plotopts = FilterRules[{opts}, Cases[Options[Plot], Except[Exclusions -> _]]]}, With[{exclusions = Join[ If[OptionValue[Exclusions] === None, {}, Flatten[{OptionValue[Exclusions]}]], PlotPiecewise`var == # & /@ Flatten[First @ exceptions]]}, With[{curves = Plot[f, domain, Evaluate @ Join[{Exclusions -> exclusions}, plotopts]]}, Show[curves, Graphics[{ColorData[1][1], EdgeForm[ColorData[1][1]], OptionValue[PlotStyle] /. Automatic -> {}, MapThread[ Map, {{ Asymptote[#, PlotRange -> PlotRange[curves], opts] &, EmptyDot[#, opts] &, FilledDot[#, opts] & }, If[Depth[#] > 2, First[#], #] & /@ exceptions}]}]]]] ] PlotPiecewise`plot[f : HoldPattern@Piecewise[pieces_, default_], domain : {var_, a_, b_}, opts : OptionsPattern[]] := Block[{PlotPiecewise`var, PlotPiecewise`domain, PlotPiecewise`allpieces, PlotPiecewise`$discontinuous}, (* INITIALIZATION: PlotPiecewise`var; PlotPiecewise`domain; PlotPiecewise`allpieces; PlotPiecewise`$discontinuous *) PlotPiecewise`init[f, domain, opts]; Message[PlotPiecewise`debug::plot, "allpieces" -> PlotPiecewise`allpieces]; (* ThePOINTS userOF INTEREST *) With[{annotatedpoints = PlotPiecewise`annotatedPoints[ PlotPiecewise`allpieces, PlotPiecewise`domain, OptionValue["AdditionalPoints"]], plotopts = FilterRules[{opts}, Cases[Options[Plot], Except[Exclusions -interfaces> _]]]}, Message[PlotPiecewise`debug::plot, "annotatedpoints" -> annotatedpoints]; (* ANNOTATIONS *) With[{annotations = Last@Reap[ PlotPiecewise`sowAnnotations[ PlotPiecewise`allpieces, PlotPiecewise`domain, annotatedpoints], {"asymptote", "empty", "filled"}]}, Message[PlotPiecewise`debug::plot, Thread[{"asymptote", "empty", "filled"} -> annotations]]; (* PROCESS PLOT *) With[{exclusions = Join[ If[OptionValue[Exclusions] === None, {}, Flatten[{OptionValue[Exclusions]}]], PlotPiecewise`var == # & /@ Flatten[First@annotations]](*can't we use annotatedpoints?*)}, With[{curves = Plot[f, domain, Evaluate@Join[{Exclusions -> exclusions}, plotopts]]}, Show[curves, Graphics[{ColorData[1][1], EdgeForm[ColorData[1][1]], OptionValue[PlotStyle] /. Automatic -> {}, MapThread[ Map, {{Asymptote[#, PlotRange -> PlotRange[curves], opts] &, EmptyDot[#, opts] &, FilledDot[#, opts] &}, If[Depth[#] > 2, First[#], #] & /@ annotations}]}]]]] ]] ]; (* The user-interface *) PlotPiecewise[f : HoldPattern@Piecewise[pieces_, default_], domain_, opts : OptionsPattern[]] := PlotPiecewise`plot[f, domain, opts]; (* tries to expand f as a Piecewise function *) PlotPiecewise`pweMethods = {"Simplification" -> False, "EliminateConditions" -> False, "RefineConditions" -> False, "ValueSimplifier" -> None}; PlotPiecewise[f_, domain : {var_, a_, b_}, opts : OptionsPattern[]] := Block[{PlotPiecewise`graphics}, (* restrict var in PiecewiseExpand/;Reduce*) With[{pwfa0 = Assuming[varIf[# \[Element]< Realsa, PiecewiseExpand[f]]#, # - 1/2] &@Floor[a], b0 = If[# > b, #, # + 1/2] &@Ceiling[b]}, TrueQ With[{pwf = Assuming[a0 < var < b0, PiecewiseExpand[ f /. dis : PlotPiecewise`$discontinuousAll[_] :> Piecewise[ Map[ {#[[1, -1]], Replace[#[[2 ;;]], cond_ /; ! FreeQ[cond, C[_]] :> (Reduce[#, var, DeleteDuplicates@Cases[#, C[_], Infinity]] & /@ LogicalExpand[ cond /. HoldPattern[And[e__?(FreeQ[#, var] &)]] :> Reduce[And[e]]]) ]} &, List @@ Reduce[dis == C[1] && C[1] ∈ Integers && a0 < var < b0, {C[1], x}, Backsubstitution -> True]], Indeterminate], Method -> PlotPiecewise`pweMethods]]}, If[Head[pwf] === Piecewise, PlotPiecewise`graphics = PlotPiecewise`plot[pwf, domain, opts];opts], PlotPiecewise`graphics = True, PlotPiecewise`plot[ Message[PlotPiecewise::nonpw Piecewise[{{f, f];-Infinity < var < Infinity}}, Indeterminate], False]] := PlotPiecewise`graphics domain, opts]] ]]; PlotPiecewise`graphics ]; Update: PlotPiecewise now automatically tries to convert a non-Piecewise function into one using PiecewiseExpand. PiecewiseExpand will also do some simplification, such as factoring and reducing a rational function; to avoid that, pass a Piecewise function directly. PlotPiecewise will not alter the formulas in a Piecewise. Note, however, that Mathematica automatically reduces x (x - 1) / (x (x - 2)) but not (x^2 - x) / (x (x - 2)).
Clear[ PlotPiecewise, (* user interface *) PlotPiecewise`plot, (* generates the plot of a `Piecewise` function *) PlotPiecewiseDot, (* handles the end points of subdomains -- Sows empty/filled dots and asymptotes *) InteriorPoints, (* handles discontinuities in the interior of a subdomain *) PlotPiecewise`solve, (* Reduce + postprocessing, to handle more general Piecewise conditions *) PlotPiecewise`expand]; (* Used by PlotPiecewise`solve to expand generated parameter C[1] *) PlotPiecewise::usage = "PlotPiecewise[Piecewise[...], {x, a, b}, opts]"; PlotPiecewise::limindet = "Limit `` is not numeric or infinite at ``"; PlotPiecewise::nonpw = "Function `` is not a Piecewise function or did not expand to one"; Options[PlotPiecewise] = Join[{"DotSize" -> Automatic, "EmptyDotStyle" -> Automatic, "FilledDotStyle" -> Automatic, "AsymptoteStyle" -> Automatic, "BaseDotSize" -> Offset[{2, 2}]}, Options[Plot]]; Options[EmptyDot] = Options[FilledDot] = Options[Asymptote] = Options[PlotPiecewise`plot] = Options[PlotPiecewise]; (* graphics elements *) EmptyDot[pt_, opts : OptionsPattern[]] := {White, OptionValue["EmptyDotStyle"] /. Automatic -> {}, Disk[pt, OptionValue["DotSize"] /. Automatic -> OptionValue["BaseDotSize"]]}; FilledDot[pt_, opts : OptionsPattern[]] := {OptionValue["FilledDotStyle"] /. Automatic -> {}, Disk[pt, OptionValue["DotSize"] /. Automatic -> OptionValue["BaseDotSize"]]}; Asymptote[x0_, opts : OptionsPattern[]] := {Dashing[Large], OptionValue["AsymptoteStyle"] /. Automatic -> {}, Line[Thread[{x0, OptionValue[PlotRange][[2]]}]]}; (* PlotPieceDot - Sows piecewise breaks, tagged with three ids; "filled" -> {x,y}; "empty" -> {x,y}; "asymptote" -> x; An entry in a Piecewise function has the form: piece = {formula, condition} *) (* some constants *) $filledRelations = Equal | LessEqual | GreaterEqual; $emptyRelations = Greater | Less; $inequality = Greater | Less | LessEqual | GreaterEqual; (* auxiliary function: causes Conditional solutions to expand to all possibilities; (arises from trig eq, and C[1] -- perhaps C[2], etc? *) PlotPiecewise`expand[cond_Or, var_] := PlotPiecewise`expand[#, var] & /@ cond; PlotPiecewise`expand[cond_, var_] := Reduce[cond, var, Backsubstitution -> True]; PlotPiecewise`solve[eq_, var_] := {var -> (var /. #)} & /@ List @ ToRules @ PlotPiecewise`expand[ Reduce[eq, var, Reals, Backsubstitution -> True], var] /. {False -> {}}; (* PlotPiecewiseDot -- Calls auxiliary function InteriorPoints Breaks down compound inequalities into simple inequalities From simple inequalities, determines dots/asymptotes From equalities, sows a dot, if formula is defined *) PlotPiecewiseDot[piece_] := (InteriorPoints[piece]; PlotPiecewiseDot[piece, "sow"]); PlotPiecewiseDot[{formula_, HoldPattern @ Inequality[a_, rel1_, b_, rel2_, c_]}, "sow"] := PlotPiecewiseDot[#, "sow"] & /@ {{formula, rel1[a, b]}, {formula, rel2[b, c]}}; PlotPiecewiseDot[{formula_, (rel : $inequality)[a_, b_, c_]}, "sow"] := PlotPiecewiseDot[#, "sow"] & /@ {{formula, rel[a, b]}, {formula, rel[b, c]}}; PlotPiecewiseDot[{formula_, cond_Equal}, "sow"] := With[{a = PlotPiecewise`var /. #, yy = formula /. #}, If[NumericQ[Abs[yy]], Sow[{a, yy}, "filled"]]] & /@ PlotPiecewise`solve[ cond && LessEqual @@ PlotPiecewise`domain[[{2, 1, 3}]], PlotPiecewise`var] (* check =? *); PlotPiecewiseDot[{formula_, cond : (rel : $inequality)[_, _]}, "sow"] := With[{a = PlotPiecewise`var /. #, yy = Limit[formula, First @ #, Direction -> If[MatchQ[rel, Greater | GreaterEqual], 1, -1]]}, If[Abs[yy] == Infinity, Sow[a, "asymptotes"], If[NumericQ[yy], Sow[{a, yy}, If[MatchQ[rel, $filledRelations], "filled", "empty"]], Message[PlotPiecewise::limindet, yy, a]] ]] & /@ PlotPiecewise`solve[ Equal @@ cond && LessEqual @@ PlotPiecewise`domain[[{2, 1, 3}]], PlotPiecewise`var] (* check =? *); (* auxiliary function: finds discontinuities inside intervals *) InteriorPoints[{formula_, cond_}] := With[{solns = PlotPiecewise`solve[ Denominator[formula, Trig -> True] == 0 && (cond /. {LessEqual -> Less, GreaterEqual -> Greater}) && LessEqual @@ PlotPiecewise`domain[[{2, 1, 3}]], PlotPiecewise`var]}, With[{a = PlotPiecewise`var /. #, yy = Limit[formula, First@#]}, If[Abs[yy] == Infinity, Sow[a, "asymptotes"], If[NumericQ[yy], Sow[{a, yy}, "empty"], Message[PlotPiecewise::limindet, yy, a]] ]] & /@ solns ]; (* The main plotting function *) PlotPiecewise`plot[f : HoldPattern @ Piecewise[pieces_, default_], domain : {var_, a_, b_}, opts : OptionsPattern[]] /; (PlotPiecewise`var = var; PlotPiecewise`domain = SetPrecision[domain, Infinity]; True) := With[{exceptions = Last @ Reap[ PlotPiecewiseDot[#(*,opts*)] & /@ If[default =!= Indeterminate, Append[pieces, (* add True (default) case to pieces *) {default, Reduce[Not[Or @@ (Last /@ pieces)]]}], pieces], {"asymptotes", "empty", "filled"}], plotopts = FilterRules[{opts}, Cases[Options[Plot], Except[Exclusions -> _]]]}, With[{exclusions = Join[ If[OptionValue[Exclusions] === None, {}, Flatten[{OptionValue[Exclusions]}]], PlotPiecewise`var == # & /@ Flatten[First @ exceptions]]}, With[{curves = Plot[f, domain, Evaluate @ Join[{Exclusions -> exclusions}, plotopts]]}, Show[curves, Graphics[{ColorData[1][1], EdgeForm[ColorData[1][1]], OptionValue[PlotStyle] /. Automatic -> {}, MapThread[ Map, {{ Asymptote[#, PlotRange -> PlotRange[curves], opts] &, EmptyDot[#, opts] &, FilledDot[#, opts] & }, If[Depth[#] > 2, First[#], #] & /@ exceptions}]}]]]] ] (* The user-interfaces *) PlotPiecewise[f : HoldPattern@Piecewise[pieces_, default_], domain_, opts : OptionsPattern[]] := PlotPiecewise`plot[f, domain, opts]; (* tries to expand f as a Piecewise function *) PlotPiecewise[f_, domain : {var_, a_, b_}, opts : OptionsPattern[]] /; With[{pwf = Assuming[var \[Element] Reals, PiecewiseExpand[f]]}, TrueQ @ If[Head[pwf] === Piecewise, PlotPiecewise`graphics = PlotPiecewise`plot[pwf, domain, opts]; True, Message[PlotPiecewise::nonpw, f]; False]] := PlotPiecewise`graphics Update 2015-7-13: PlotPiecewise now handles discontinuities of non-Piecewise functions. (It basically did this before, but required the head to be Piecewise or contain a built-in discontinuous function, like Sign. All I did was brainlessly wrap a function in Piecewise. I also had to rewrite some of the Reduce/PiecewiseExpand code. One of the more complicated examples, which used to expand to a number of integer cases, kept the integer parameter instead of expanding; in another (not shown), the Ceiling of a complicated function was no longer expanded into a Piecewise function.
Update: PlotPiecewise now automatically tries to convert a non-Piecewise function into one using PiecewiseExpand. PiecewiseExpand will also do some simplification, such as factoring and reducing a rational function; to avoid that, pass a Piecewise function directly. PlotPiecewise will not alter the formulas in a Piecewise. Note, however, that Mathematica automatically reduces x (x - 1) / (x (x - 2)) but not (x^2 - x) / (x (x - 2)).
New examples (2015-7-13)
From Is there any way to reveal a removable singularity in a plot?:
PlotPiecewise[(2^x - 2)/(x - 1), {x, -2, 2}, "DotSize" -> Offset[{3, 3}], "EmptyDotStyle" -> EdgeForm[Directive[ColorData[97, 1], AbsoluteThickness[1.6]]]] 
A similar one:
PlotPiecewise[(2^x - 2)/(x^2 - 1), {x, -2, 2}] 
ClearAll[PlotPiecewise, PlotPiecewise`plot, PlotPiecewise`init, PlotPiecewise`solve, PlotPiecewise`expand, PlotPiecewise`annotatedPoints, PlotPiecewise`boundaryPoints, PlotPiecewise`interiorPoints, PlotPiecewise`sowAnnotations, PlotPiecewise`inDomain]; PlotPiecewise::usage = "PlotPiecewise[Piecewise[...], {x, a, b}, opts]"; PlotPiecewise::limindet = "Limit `` is not numeric or infinite at ``"; PlotPiecewise::nonpw = "Function `` is not a Piecewise function or did not expand to one"; PlotPiecewise`debug::debug = "``"; PlotPiecewise`debug::plot = "``"; PlotPiecewise`debug::annotation = "``"; PlotPiecewise`debug::limit = "``"; PlotPiecewise`debug = Hold[PlotPiecewise`debug::debug, PlotPiecewise`debug::plot, PlotPiecewise`debug::annotation, PlotPiecewise`debug::limit]; Off @@ PlotPiecewise`debug; Options[PlotPiecewise] = Join[{"DotSize" -> Automatic, "EmptyDotStyle" -> Automatic, "FilledDotStyle" -> Automatic, "AsymptoteStyle" -> Automatic, "BaseDotSize" -> Offset[{2, 2}], "AdditionalPoints" -> {}, (* addition pts to annotate *) "PiecewiseExpand" -> Automatic, (* which fns. to expand *) "ContinuousEndpoints" -> Automatic},(* eval. formula, not limit *) Options[Plot]]; Options[EmptyDot] = Options[FilledDot] = Options[Asymptote] = Options[PlotPiecewise`plot] = Options[PlotPiecewise`init] = Options[PlotPiecewise]; (* graphics elements *) Clear[EmptyDot, FilledDot, Asymptote]; EmptyDot[pt_, opts : OptionsPattern[]] /; OptionValue["EmptyDotStyle"] === None := {}; FilledDot[pt_, opts : OptionsPattern[]] /; OptionValue["FilledDotStyle"] === None := {}; Asymptote[pt_, opts : OptionsPattern[]] /; OptionValue["AsymptoteStyle"] === None := {}; EmptyDot[pt_, opts : OptionsPattern[]] := {White, OptionValue["EmptyDotStyle"] /. Automatic -> {}, Disk[pt, OptionValue["DotSize"] /. Automatic -> OptionValue["BaseDotSize"]]}; FilledDot[pt_, opts : OptionsPattern[]] := {OptionValue["FilledDotStyle"] /. Automatic -> {}, Disk[pt, OptionValue["DotSize"] /. Automatic -> OptionValue["BaseDotSize"]]}; Asymptote[x0_, opts : OptionsPattern[]] := {Dashing[Large], OptionValue["AsymptoteStyle"] /. Automatic -> {}, Line[Thread[{x0, OptionValue[PlotRange][[2]]}]]}; PlotPiecewise`$inequality = Greater | Less | LessEqual | GreaterEqual; PlotPiecewise`$discontinuousAuto = Ceiling | Floor | Round | Sign; PlotPiecewise`$discontinuousAll = Ceiling | Floor | Round | Sign |(*Min|Max|Clip|*)UnitStep | IntegerPart |(*FractionalPart|*)Mod | Quotient | UnitBox | UnitTriangle | SquareWave(*|TriangleWave|SawtoothWave*)(*|BernsteinBasis|\ BSplineBasis|Abs|If|Which|Switch*); PlotPiecewise`$discontinuous = Ceiling | Floor | Round | Sign; (* auxiliary functions*) (* causes Conditional solutions to expand to all possibilities; (arises from trig eq, and C[1] -- perhaps C[2], etc? *) PlotPiecewise`expand[cond_Or, var_] := PlotPiecewise`expand[#, var] & /@ cond; PlotPiecewise`expand[cond_, var_] := Reduce[cond, var, Backsubstitution -> True]; PlotPiecewise`solve[eq_, var_] /; MemberQ[eq, PlotPiecewise`$discontinuous, Infinity, Heads -> True] := PlotPiecewise`solve[# == C[1] && C[1] ∈ Integers && And @@ Cases[eq, Except[_Equal]], var] & /@ Cases[eq, PlotPiecewise`$discontinuous[e_] :> e, Infinity]; PlotPiecewise`solve[eq_, var_] := {var -> (var /. #)} & /@ List@ToRules@ PlotPiecewise`expand[ Reduce[eq, var, Reals, Backsubstitution -> True], var] /. {False -> {}}; (* limit routines for handling discontinuous functions, which Limit fails to do *) Needs["NumericalCalculus`"]; PlotPiecewise`nlimit[f_?NumericQ, var_ -> x0_, dir_] := f; PlotPiecewise`nlimit[f_, var_ -> x0_, dir_] := NLimit[f, var -> x0, dir]; PlotPiecewise`limit[f_, var_ -> x0_, dir_] /; MemberQ[Numerator[f], PlotPiecewise`$discontinuous, Infinity, Heads -> True] := Module[{y0, f0}, f0 = f //. (disc : PlotPiecewise`$discontinuous)[z_] /; FreeQ[z, PlotPiecewise`$discontinuous] :> disc[ With[{dz = Abs[D[z, var] /. var -> N@x0]}, Mean[{z /. var -> N@x0, z /. var -> x0 - 0.1 Last[dir]/Max[1, dz]}]] ]; Message[PlotPiecewise`debug::limit, {f0, f, var -> x0, dir}]; Quiet[Check[y0 = PlotPiecewise`nlimit[f0, var -> x0, dir], Check[y0 = Limit[f0, var -> x0, dir], If[! NumericQ[y0], y0 = Indeterminate]]], {Power::infy, Infinity::indet, NLimit::noise}]; y0 ]; PlotPiecewise`limit[f_, var_ -> x0_, dir_] := Module[{y0}, Quiet[Check[y0 = f /. var -> x0, Check[y0 = Limit[f, var -> x0, dir], If[! NumericQ[y0], y0 = Indeterminate]]], {Power::infy, Infinity::indet}]; y0 ]; PlotPiecewise`$reverseIneq = {Less -> Greater, Greater -> Less, LessEqual -> GreaterEqual}; PlotPiecewise`reverseIneq[(rel : PlotPiecewise`$inequality)[ args__]] := (rel /. PlotPiecewise`$reverseIneq) @@ Reverse@{args}; PlotPiecewise`inDomain[] := LessEqual @@ PlotPiecewise`domain[[{2, 1, 3}]]; PlotPiecewise`inDomain[dom_] := LessEqual @@ dom[[{2, 1, 3}]]; (* annotatedPoints -- returns list of abscissas to be "annotated" with dots/asymptotes boundaryPoints -- returns list of boundaries numbers between \ pieces interiorPoints -- returns list of points where the \ denominator is zero *) PlotPiecewise`annotatedPoints[allpieces_, domain_, additionalpoints_] := DeleteDuplicates@Flatten@Join[ PlotPiecewise`boundaryPoints[allpieces, domain], PlotPiecewise`interiorPoints[allpieces, domain], additionalpoints ]; PlotPiecewise`boundaryPoints[allpieces_, domain : {var_, _, _}] := With[{conditions = DeleteDuplicates[ Equal @@@ Flatten[Last /@ allpieces /. {HoldPattern@ Inequality[a_, rel1_, b_, rel2_, c_] :> {PlotPiecewise`reverseIneq[rel1[a, b]], rel2[b, c]}, (rel : PlotPiecewise`$inequality)[a_, b_, c_] :> {PlotPiecewise`reverseIneq[rel[a, b]], rel[b, c]}} ]]}, Message[PlotPiecewise`debug::annotation, conditions]; var /. Flatten[ (* deletes no soln {}'s *) PlotPiecewise`solve[# && PlotPiecewise`inDomain[domain], var] & /@ conditions, 1] /. var -> {} (* no BPs in domain *) ]; PlotPiecewise`interiorPoints[allpieces_, domain : {var_, _, _}] := MapThread[ Function[{formula, condition}, Flatten[ {With[{solns = PlotPiecewise`solve[ Denominator[formula, Trig -> True] == 0 && (condition /. {LessEqual -> Less, GreaterEqual -> Greater}) && LessEqual @@ PlotPiecewise`domain[[{2, 1, 3}]], PlotPiecewise`var]}, PlotPiecewise`var /. solns /. PlotPiecewise`var -> {} ], If[MemberQ[Numerator[formula], PlotPiecewise`$discontinuous, Infinity, Heads -> True], With[{solns = PlotPiecewise`solve[ Numerator[formula] == 0 && (condition /. {LessEqual -> Less, GreaterEqual -> Greater}) && LessEqual @@ PlotPiecewise`domain[[{2, 1, 3}]], PlotPiecewise`var]}, PlotPiecewise`var /. solns /. PlotPiecewise`var -> {} ], {} ]} ]], Transpose@allpieces ]; (* sowAnnotations - Sows irregular points, tagged with three ids; "filled" \[Rule] {x,y}; "empty" \[Rule] {x,y}; "asymptote" \[Rule] x; *) PlotPiecewise`sowAnnotations[allpieces_, domain : {var_, a_, b_}, {}] := {}; PlotPiecewise`sowAnnotations[allpieces_, domain : {var_, a_, b_}, points_List] := (Message[PlotPiecewise`debug::annotation, "sowAnn" -> {allpieces, points}]; PlotPiecewise`sowAnnotations[allpieces, domain, ##] & @@@ Partition[{If[First[#] == a, Indeterminate, a]}~Join~#~ Join~{If[Last[#] == b, Indeterminate, b]}, 3, 1] &@ SortBy[points, N]); PlotPiecewise`sowAnnotations[allpieces_, domain : {var_, _, _}, xminus_, x0_?NumericQ, xplus_] := Module[{y0, yplus, yminus, f0, fminus, fplus}, f0 = First[ Pick @@ MapAt[# /. var -> x0 & /@ # &, Transpose@allpieces, 2] /. {} -> {Indeterminate}]; Quiet[y0 = f0 /. var -> N@x0, {Power::infy, Infinity::indet}]; If[xminus =!= Indeterminate, (* xminus ≠ left endpoint *) fminus = First[Pick @@ MapAt[# /. var -> Mean[{xminus, x0}] & /@ # &, Transpose@allpieces, 2] /. {} -> {Indeterminate}]; yminus = PlotPiecewise`limit[fminus, var -> x0, Direction -> 1]; ]; If[xplus =!= Indeterminate, (* xplus ≠ right endpoint *) fplus = First[ Pick @@ MapAt[# /. var -> Mean[{x0, xplus}] & /@ # &, Transpose@allpieces, 2] /. {} -> {Indeterminate}]; yplus = PlotPiecewise`limit[fplus, var -> x0, Direction -> -1]; ]; If[Abs[yminus] == Infinity || Abs[yplus] == Infinity, Sow[x0, "asymptote"]]; If[NumericQ[y0], Sow[{x0, y0}, "filled"]]; Message[ PlotPiecewise`debug::annotation, {{x0, y0, f0}, {xminus, yminus, fminus}, {xplus, yplus, fplus}}]; Sow[{x0, #}, "empty"] & /@ DeleteDuplicates@DeleteCases[Select[{yminus, yplus}, NumericQ], y0] ]; (* initialization of context variables *) PlotPiecewise`init[f : HoldPattern@Piecewise[pieces_, default_], domain : {var_, _, _}, opts : OptionsPattern[]] := (PlotPiecewise`domain = SetPrecision[domain, Infinity]; PlotPiecewise`var = var; PlotPiecewise`allpieces = If[default =!= Indeterminate, Append[pieces,(* add True case to pieces *) {default, If[Head[#] === Not, Reduce[#], #] &@ Simplify[Not[Or @@ (Last /@ pieces)]]}], pieces] /. {formula_, HoldPattern@Or[e__]} :> Sequence @@ ({formula, #} & /@ List[e]); PlotPiecewise`$discontinuous = OptionValue[ "PiecewiseExpand"] /. {Automatic -> PlotPiecewise`$discontinuousAuto, All -> PlotPiecewise`$discontinuousAll, None -> {}}; Message[PlotPiecewise`debug::debug, "f" -> f] ); (* The main plotting function *) PlotPiecewise`plot[f : HoldPattern@Piecewise[pieces_, default_], domain : {var_, a_, b_}, opts : OptionsPattern[]] := Block[{PlotPiecewise`var, PlotPiecewise`domain, PlotPiecewise`allpieces, PlotPiecewise`$discontinuous}, (* INITIALIZATION: PlotPiecewise`var; PlotPiecewise`domain; PlotPiecewise`allpieces; PlotPiecewise`$discontinuous *) PlotPiecewise`init[f, domain, opts]; Message[PlotPiecewise`debug::plot, "allpieces" -> PlotPiecewise`allpieces]; (* POINTS OF INTEREST *) With[{annotatedpoints = PlotPiecewise`annotatedPoints[ PlotPiecewise`allpieces, PlotPiecewise`domain, OptionValue["AdditionalPoints"]], plotopts = FilterRules[{opts}, Cases[Options[Plot], Except[Exclusions -> _]]]}, Message[PlotPiecewise`debug::plot, "annotatedpoints" -> annotatedpoints]; (* ANNOTATIONS *) With[{annotations = Last@Reap[ PlotPiecewise`sowAnnotations[ PlotPiecewise`allpieces, PlotPiecewise`domain, annotatedpoints], {"asymptote", "empty", "filled"}]}, Message[PlotPiecewise`debug::plot, Thread[{"asymptote", "empty", "filled"} -> annotations]]; (* PROCESS PLOT *) With[{exclusions = Join[ If[OptionValue[Exclusions] === None, {}, Flatten[{OptionValue[Exclusions]}]], PlotPiecewise`var == # & /@ Flatten[First@annotations]](*can't we use annotatedpoints?*)}, With[{curves = Plot[f, domain, Evaluate@Join[{Exclusions -> exclusions}, plotopts]]}, Show[curves, Graphics[{ColorData[1][1], EdgeForm[ColorData[1][1]], OptionValue[PlotStyle] /. Automatic -> {}, MapThread[ Map, {{Asymptote[#, PlotRange -> PlotRange[curves], opts] &, EmptyDot[#, opts] &, FilledDot[#, opts] &}, If[Depth[#] > 2, First[#], #] & /@ annotations}]}]]]] ]] ]; (* The user-interface *) PlotPiecewise[f : HoldPattern@Piecewise[pieces_, default_], domain_, opts : OptionsPattern[]] := PlotPiecewise`plot[f, domain, opts]; (* tries to expand f as a Piecewise function *) PlotPiecewise`pweMethods = {"Simplification" -> False, "EliminateConditions" -> False, "RefineConditions" -> False, "ValueSimplifier" -> None}; PlotPiecewise[f_, domain : {var_, a_, b_}, opts : OptionsPattern[]] := Block[{PlotPiecewise`graphics}, (* restrict var in PiecewiseExpand/Reduce*) With[{a0 = If[# < a, #, # - 1/2] &@Floor[a], b0 = If[# > b, #, # + 1/2] &@Ceiling[b]}, With[{pwf = Assuming[a0 < var < b0, PiecewiseExpand[ f /. dis : PlotPiecewise`$discontinuousAll[_] :> Piecewise[ Map[ {#[[1, -1]], Replace[#[[2 ;;]], cond_ /; ! FreeQ[cond, C[_]] :> (Reduce[#, var, DeleteDuplicates@Cases[#, C[_], Infinity]] & /@ LogicalExpand[ cond /. HoldPattern[And[e__?(FreeQ[#, var] &)]] :> Reduce[And[e]]]) ]} &, List @@ Reduce[dis == C[1] && C[1] ∈ Integers && a0 < var < b0, {C[1], x}, Backsubstitution -> True]], Indeterminate], Method -> PlotPiecewise`pweMethods]]}, If[Head[pwf] === Piecewise, PlotPiecewise`graphics = PlotPiecewise`plot[pwf, domain, opts], PlotPiecewise`graphics = PlotPiecewise`plot[ Piecewise[{{f, -Infinity < var < Infinity}}, Indeterminate], domain, opts]] ]]; PlotPiecewise`graphics ]; 