To find the area of these points, we first must convert to a projected coordinate system. Since your points lie in multiple state plane systems, we'll use UTM zone 11 to convert your latitude longitudes.
Here are the points courtesy of new Wolfram Language functions...
latlons = {{32.6123, -117.041}, {40.6973, -111.9}, {34.0276, -118.046}, {40.8231, -111.986}, {34.0446, -117.94}, {33.7389, -118.024}}; GeoGraphics[GeoMarker/@latlons] 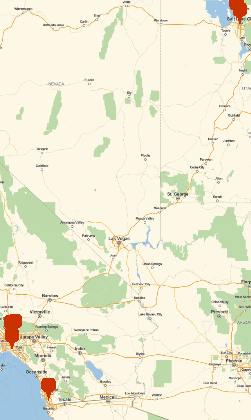
To do the conversion:
utm = GeoGridPosition[GeoPosition[#], "UTMZone11"][[1]] & /@ latlons
{{-3848.25, 3.60975*10^6}, {431132., 4.51949*10^6}, {-96605.2, 3.76722*10^6}, {423059., 4.53305*10^6}, {-86797.8, 3.76901*10^6}, {-94892.4, 3.73517*10^6}}
This returns coordinates in meters.
Graphics`Mesh`MeshInit[]; PolygonArea[utm]
7.43416*10^10
And let's convert to acres, lazily...
UnitConvert[Quantity[%, "meters squared"], "acres"]
1.83701*10^7 acres
Even so, these points are spread far apart in a strange order across multiple defined projected areas, so the area calculation may not be as accurate as possible.
