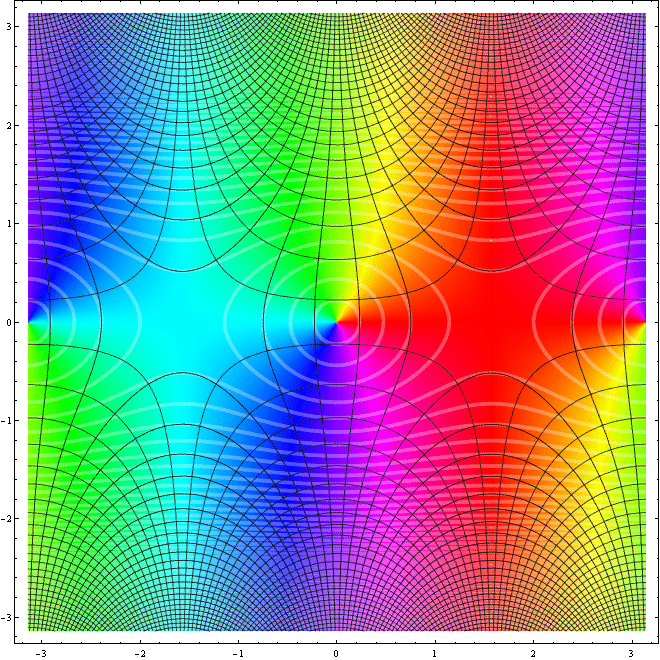
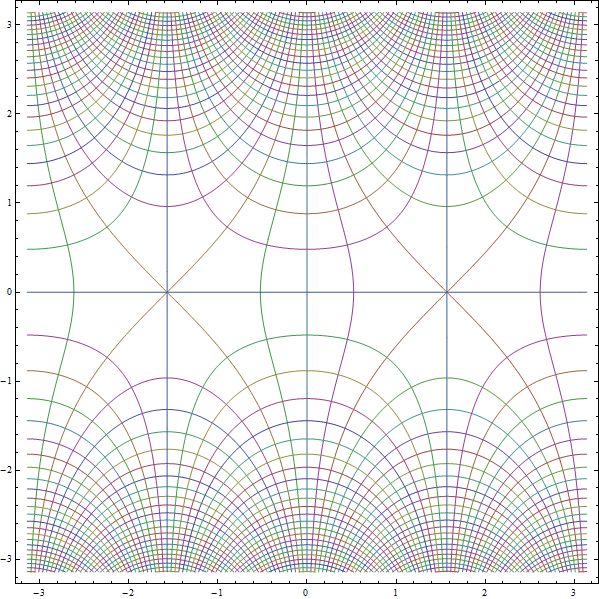
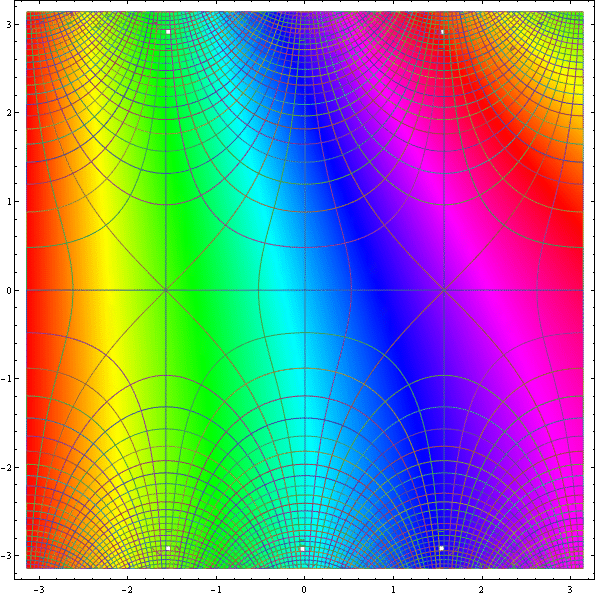
This seemsis a good way :
DensityPlot[ -(1/2)Rescale[ Arg[Sin[xArg[Sin[-x +- I y]], {-Pi, Pi}], {x, -Pi, Pi}, {y, -Pi, Pi}, MeshFunctions -> Function @@@ {{{x, y, z}, Re[Sin[x + I y]]}, {{x, y, z}, Im[Sin[x + I y]]}, {{x, y, z}, Abs[Sin[x + I y]]}}, MeshStyle -> {Directive[Gray, Opacity[0Directive[Opacity[0.8], Thickness[0.001]], Directive[Gray, Opacity[0Directive[Opacity[0.7], Thickness[0.001]], Directive[White, Opacity[0.7]3], Thickness[0.005]]006]]}, ColorFunction -> Hue, Mesh -> 50, Exclusions -> None, PlotPoints -> 100]