Sadly the undocumented mechanism behind Simon's splitstyle no longer works in Mathematica 10.0 or 10.1. Post-processing(1)(1),(2)(2) remains an option as does use of ListPlotuse of ListPlot. While pure post-processing is possible, in a bid to make this answer unique I shall instead define styleSplitter as a function that extracts the PlotStyle option from an unevaluated Plot expression. If none is present the default for that plot type is taken from Options.
(This function can be viewed as a derivative of xslittlegrass's restylePlot2xslittlegrass's restylePlot2 that pulls style information from the Plot expression itself.)
SetAttributes[styleSplitter, HoldFirst] styleSplitter[plot : h_[___, op : OptionsPattern[]]] := MapAt[ ListLinePlot[Cases[Normal @ #, Line[x__] :> x, -3] , PlotRange -> Full , PlotStyle -> OptionValue[h, {op}, PlotStyle] ][[1]] & , plot , 1 ] Test:
g[y_] := Total[Table[1, {z, 1, Round[y + 1]}]]; Plot[ Table[g[x*n], {n, 1, 3}], {x, 0, 1}, PlotStyle -> {Blue, Orange} ] // styleSplitter 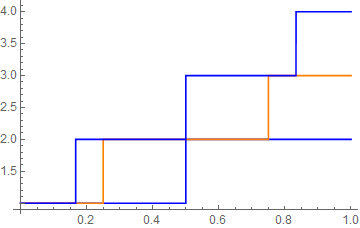
Because styling is done by ListLinePlot itself automatic behaviors such as style cycling are preserved.
