The first thing I did was to rationalizing all calculations, starting with the defintion of σ and minroot. This stops the Solve::ratnz messages. I also made some other improvements to minroot.

σ = 6/10; minroot[gg_?NumericQ, bb_?NumericQ] := Module[{b, g, rts, r}, b = Rationalize[bb, 0]; g = Rationalize[gg, 0]; rts = r /. Solve[ 1 - (b/r)^2 - g^-2*(2/15*σ^9 (1/(r - 1)^9 - 1/(r + 1)^9 - 9/(8 r) (1/(r - 1)^8 - 1/(r + 1)^8)) - σ^3 (1/(r - 1)^3 - 1/(r + 1)^3 - 3/(2 r) (1/(r - 1)^2 - 1/(r + 1)^2))) == 0, r]; Max[Select[rts, Im[#] == 0 && # > 0 &]]] 

The definition of aA is more or less untouched.

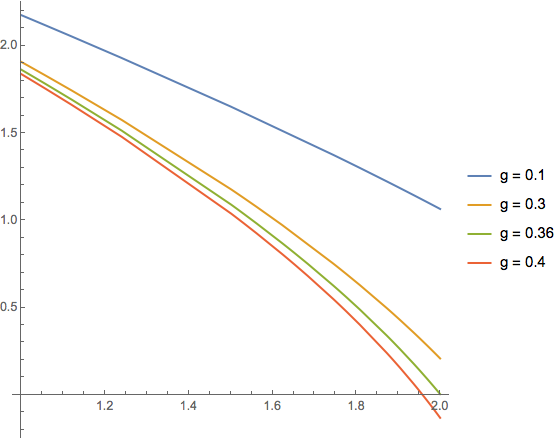
aA[g_?NumberQ, b_?NumberQ, i_] := Pi - 2 b NIntegrate[ 1/(r^2* Sqrt[ 1 - (b/r)^2 - g^(-2)* (2/15*σ^9 (1/(r - 1)^9 - 1/(r + 1)^9 - 9/(8 r) * (1/(r - 1)^8 - 1/(r + 1)^8)) - σ^3 (1/(r - 1)^3 -1/(r + 1)^3 -3/(2 r) * (1/(r - 1)^2 - 1/(r + 1)^2)))]), {r, minroot[g, b], ∞}, Exclusions -> {r^2*Sqrt[1 - (b/r)^2 - g^(-2)* (2/15*σ^9 (1/(r - 1)^9 - 1/(r + 1)^9 - 9/(8 r) * (1/(r - 1)^8 - 1/(r + 1)^8)) - σ^3 (1/(r - 1)^3 - 1/(r + 1)^3 - 3/(2 r) * (1/(r - 1)^2 - 1/(r + 1)^2)))] == 0}, MaxRecursion -> i, Method -> {Automatic, "SymbolicProcessing" -> False}] 

A plot of aA over the interval [1, 2] for several values of g shows the problem with small values of g.

Plot[Evaluate[Re[aA[#, b, 5]]& /@ #], {b, 1, 2}, PlotPoints -> 5, PlotRange -> {-.25, 2.25}, PlotLegends -> Evaluate[( Style[Row[{"g = ", #}], 12]&) /@ #], AspectRatio -> 1, ImageSize -> Medium]&[{.1, .3, .36, .4}] 

We now know why rootmin fails for g < .36116; however, using the version of minroot shown above, rootmin produces no messages for values of g >= .36116. I do recommend simplifying it as shown below.

rootmin[g_?NumberQ] := Module[{b}, b /. FindRoot[Re[aA[g, b, 5]] == 0, {b, 1, 2}, Method -> "Brent"]] rootmin[.36116] 

2. 

That is, the zero falls right at the end of the interval.