Since someone dragged in Canada...

Here is the code from a MathGroup post I had referenced. I have modified to compile to C and that speeds it further. The one-off preprocessing does take time but it seems not unreasonable. It takes a list of lists of polygons (so the "region" need not be connected). To account for this I slightly alter the setup from Mac's response.

Preprocessing the polygon:

getSegsC = Compile[{{j, _Integer}, {minx, _Real}, {len, _Real}, {eps, _Real}, \ {segs, _Real, 3}}, Module[{lo, hi}, lo = minx + (j - 1)*len - eps; hi = minx + j*len + eps; Select[segs, Module[{xlo, xhi}, {xlo, xhi} = Sort[{#[[1, 1]], #[[2, 1]]}]; lo <= xlo <= hi || lo <= xhi <= hi || (xlo <= lo && xhi >= hi)] &]]]; polyToSegmentList[poly_, nbins_] := Module[{xvals, yvals, minx, maxx, miny, maxy, segments, flatsegments, segmentbins, xrange, len, eps}, {xvals, yvals} = Transpose[Flatten[poly, 1]]; {minx, maxx} = {Min[xvals], Max[xvals]}; {miny, maxy} = {Min[yvals], Max[yvals]}; segments = Map[Partition[#, 2, 1, {1, 1}] &, poly]; flatsegments = Flatten[segments, 1]; xrange = maxx - minx; eps = 1/nbins*len; len = xrange/nbins; segmentbins = Table[getSegsC[j, minx, len, eps, flatsegments], {j, nbins}]; {{minx, maxx}, {miny, maxy}, segmentbins}] 

The actual in-or-out code.

pointInPolygon[{x_, y_}, bins_, xmin_, xmax_, ymin_, ymax_] := Catch[Module[{nbins = Length[bins], bin}, If[x < xmin || x > xmax || y < ymin || y > ymax, Throw[False]]; bin = Ceiling[nbins*(x - xmin)/(xmax - xmin)]; If[EvenQ[countIntersectionsC[bins[[bin]], x, y, ymin - 1.]], False, True]]] countIntersectionsC = Compile[{{segs, _Real, 3}, {x, _Real}, {yhi, _Real}, {ylo, _Real}}, Module[{tally = 0, yval, xlo, xhi, y1, y2}, Do[{{xlo, y1}, {xhi, y2}} = segs[[j]]; If[(x < xlo && x < xhi) || (x > xlo && x > xhi), Continue[]]; yval = y1 + (x - xlo)/(xhi - xlo)*(y2 - y1); If[ylo < yval < yhi, tally++];, {j, Length[segs]}]; tally]]; 

The mainland of Canada will be the test again. As in Mac's example I rescale so coordinates are all between -1 and 1. This means I really don't need the x/ymin/max stuff but I opted to keep that in.

p = CountryData["Canada", "Polygon"][[1, 1]]; poly = {Transpose[{Rescale[ p[[All, 1]], {Min@#, Max@#} &@p[[All, 1]], {-1, 1}], Rescale[p[[All, 2]], {Min@#, Max@#} &@p[[All, 2]], {-1, 1}]}]}; 

I'll use 1000 bins and do the preprocessing.

nbins = 1000; Timing[{{xmin, xmax}, {ymin, ymax}, segmentbins} = polyToSegmentList[poly, nbins];] (* Out[369]= {5.15, Null} *) 

For testing I'll take 20000 points.

npts = 20000; pts = Partition[RandomReal[{-1, 1}, npts], 2]; Timing[ inout = Map[pointInPolygon[#, segmentbins, xmin, xmax, ymin, ymax] &, pts];] (* Out[402]= {0.37, Null} *) 

Visual check:

ListPlot[Pick[pts, inout], Joined -> False]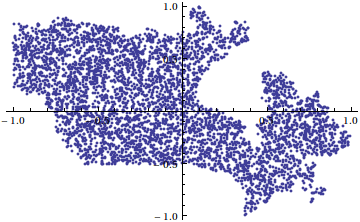 

The northeast reminds me a bit of the duck's head seen here. But then...I've always found the Baffin...to be bafflin'.