13
$\begingroup$

Consider a self-intersecting non-convex polygon:

points = {{0, 0}, {2, 0}, {11, 4}, {-1, 4}, {4, .5}, {6, 7}, {7, 0}, {10, 0}, {10, 6}, {0, 6}};

I need to find the polygon's outer boundary (in red):

boundary={{0,0},{2,0},{3.660194174757282,0.7378640776699029},{4,0.5},{4.138613861386139,0.9504950495049506},{6.701492537313434,2.0895522388059704},{7,0},{10,0},{10,3.555555555555556},{10,4},{10,6},{6.142857142857142,6},{6,7},{5.692307692307692,6},{5.692307692307692,6},{0,6},{0,4},{-1,4},{0,3.3000000000000003}}; { Graphics@Thread@Line@Transpose[{points, RotateLeft@points}], Graphics@{Red, Thread@Line@Transpose[{boundary, RotateLeft@boundary}]} }

enter image description here

WindingPolygon, OuterPolygon and their combinations fail:

{ Graphics@Thread@Line@Transpose[{#,RotateLeft@#}]&@WindingPolygon[points][[1]], Graphics@Thread@Line@Transpose[{#,RotateLeft@#}]&@OuterPolygon[Polygon@points][[1]], Graphics@Thread@Line@Transpose[{#,RotateLeft@#}]&@OuterPolygon[WindingPolygon[points]][[1]] }

enter image description here

What is the proper way to solve this problem?

Improve this question
$\endgroup$

4 Answers 4

Reset to default
7
$\begingroup$

Apply my function contourPolygon on coordinates of a polygon. (output is already a polygon)

Use preset tms variable from @Anton answer.

contourPolygon[x_] := Polygon[#[[1]][[First@FirstCase[#, _Rule, {#[[2]]}, All]]]] &@ CrossingPolygon[x] Graphics[{EdgeForm[White], Polygon[#], FaceForm[None], EdgeForm[{Green}], contourPolygon[#]}] & /@ tms // Multicolumn[#, Background -> Gray] &

enter image description here

Improve this answer
$\endgroup$
7
  • $\begingroup$ Now we're talking $\endgroup$ Commented Nov 12, 2024 at 4:48
  • $\begingroup$ How come this CrossingPolygon functionality is not mentioned anywhere in documentation? CrossingPolygon[points][[2]] gives all that is necessary, but is somehow omitted Help. $\endgroup$ Commented Nov 12, 2024 at 8:08
  • $\begingroup$ @cvgmt Yes, but may not work for some special cases, like for example points {{0, 0}, {0, 1}, {1, 0}, {1, 1}}. $\endgroup$ Commented Nov 12, 2024 at 10:24
  • $\begingroup$ @cvgmt In fact your code does not work. Look at Graphics[{EdgeForm[Red], CrossingPolygon[tm9] /. Rule[a_, b_] :> a}] or instead of tm9 use tm1 or tm2. $\endgroup$ Commented Nov 12, 2024 at 10:38
  • $\begingroup$ @Anton I agree, the second argument of output of CrossingPolygon is not well explained in the documentation. Also notice that code in cvgmt's comment above does not work as can be seen by code in my previous comment. $\endgroup$ Commented Nov 12, 2024 at 10:42
11
$\begingroup$ 
points = {{0, 0}, {2, 0}, {11, 4}, {-1, 4}, {4, .5}, {6, 7}, {7, 0}, {10, 0}, {10, 6}, {0, 6}}; poly = Polygon@points; pts = RegionUnion[poly, DiscretizeRegion@OuterPolygon@poly] // MeshPrimitives[#, 0] & // Map[Apply[Sequence]] Graphics[{Lighter@Yellow, Polygon@pts, Red, Point@pts, Black, Line@(Join[pts, {First@pts}])}]

polygon showing outer boundary method-1

Using RegionBoundary:

pts = DiscretizeRegion[poly] // RegionBoundary // MeshPrimitives[#, 0] & // Map[Apply[Sequence]]; fst = FindShortestTour[pts]; pts[[Last@fst]] // Graphics[{Lighter@Green, Polygon@#, Red, Point@#}] &

polygon showing outer boundary method-2

Improve this answer
$\endgroup$
5
  • $\begingroup$ RegionUnion[poly, OuterPolygon@poly] does not work on my system (WM 14.0 Windows). $\endgroup$ Commented Nov 9, 2024 at 19:31
  • $\begingroup$ In computing pts in the first set of codes, the following error occurs: Part::partw: Part 2 of Line[{{{-1.,4.},{0.,3.3}},{{0.,0.},{2.,0.}},{{0.,3.3},{0.,0.}},{{3.66019,0.737864},{4.,0.5}},{{<<18>>,<<3>>},<<1>>},<<1>>,{{6.14286,6.},{6.42857,4.}},{{6.42857,4.},{6.70149,2.08955}},{{7.,0.},{10.,0.}},{{10.,3.55556},{11.,4.}}}] does not exist. "14.1.0 for Mac OS X ARM (64-bit) (July 16, 2024)" $\endgroup$ Commented Nov 10, 2024 at 4:52
  • $\begingroup$ Sorry about the omission. I have updated the first answer to include DiscretizeRegion. $\endgroup$ Commented Nov 10, 2024 at 5:04
  • $\begingroup$ RegionUnion[poly, DiscretizeRegion@OuterPolygon@poly] crashes on 14.0 $\endgroup$ Commented Nov 10, 2024 at 6:21
  • $\begingroup$ I use v12.2 so can't say that I know how to fix/alter it for more recent versions. $\endgroup$ Commented Nov 10, 2024 at 6:42
7
$\begingroup$

  • We add a large Rectangle which contain the Polygon and use RegionDifference to clip the Polygon.

  • After that we use InnerPolygon to get the "boundary" desired region.

  • I test this method in version 12.2,12.3, 13.3.1,14.0 but does not work in 14.1, it is a bug of 14.1 since the result of RegionDifference is wrong.

rectangle = Rectangle @@ Transpose@CoordinateBounds[Transpose@RegionBounds[poly], 1.5]; regout = BoundaryMesh[rectangle]; reg = RegionDifference[regout, poly]; regin = InnerPolygon[reg]; {regout, Region@poly, reg} Graphics[{Red, RegionBoundary[regin]}]
  • The correct result of RegionDifference should be (version 13.3.1 and 14.0 is right, version 12.2,12.3 and 14.1 is wrong)
  • For version 12.2 and 12.3, when we set poly = WindingPolygon[points, "NonzeroRule"]; then all the result is correct.

enter image description here

enter image description here

  • If we don't not want to use InnerPolygon, we can also extract the MeshCells in the region.
MeshRegion[MeshCoordinates[reg], MeshCells[reg, 1, "Multicells" -> True][[2]]]

or

BoundaryMeshRegion[MeshCoordinates[reg], MeshCells[reg, 1, "Multicells" -> True][[2]]] // RegionBoundary

enter image description here

Improve this answer
$\endgroup$
5
  • $\begingroup$ regin is EmptyRegion[2] on 14.1.0 for Mac OS X ARM (64-bit) (July 16, 2024). $\endgroup$ Commented Nov 10, 2024 at 4:48
  • $\begingroup$ @A.Kato Since RegionDifference is wrong in version 14.1 $\endgroup$ Commented Nov 10, 2024 at 5:01
  • $\begingroup$ For version 14.1, we have to use ImageMesh. Clear[points, poly, rectangle, g]; points = {{0, 0}, {2, 0}, {11, 4}, {-1, 4}, {4, .5}, {6, 7}, {7, 0}, {10, 0}, {10, 6}, {0, 6}}; poly = WindingPolygon[points, "NonzeroRule"]; rectangle = Rectangle @@ Transpose@CoordinateBounds[points, .5]; g = Graphics[{rectangle, White, poly}] // ImageMesh; BoundaryMeshRegion[MeshCoordinates[g], MeshCells[g, 1, "Multicells" -> True][[2]]] // RegionBoundary $\endgroup$ Commented Nov 10, 2024 at 8:40
  • $\begingroup$ @cvgmt ImageMesh does not give a precise solution. $\endgroup$ Commented Nov 11, 2024 at 8:32
  • $\begingroup$ @Anton That is why I just add a comments. $\endgroup$ Commented Nov 11, 2024 at 9:47
3
$\begingroup$

Here's a more generalized solution, based on @cvgmt's approach.

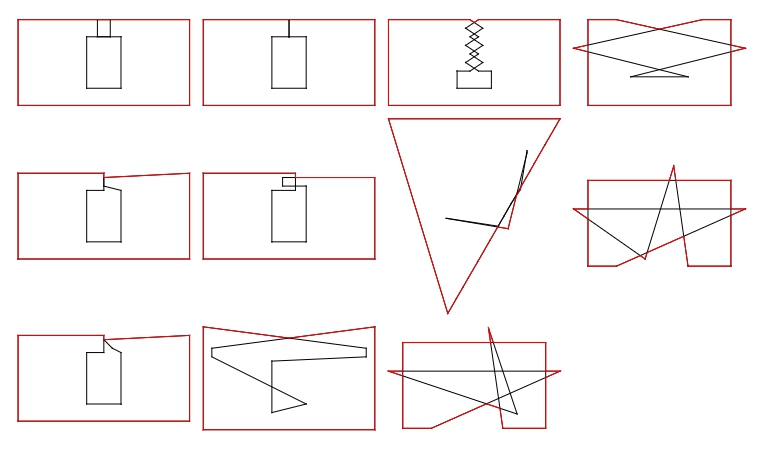
Toy models:

tm1={{-10,-5},{10,-5},{10,5},{-0.75,5},{-0.75,3},{2,3},{2,-3},{-2,-3},{-2,3},{0.75,3},{0.75,5},{-10,5}}; tm2={{-10,-5},{10,-5},{10,5},{0,4.5},{0,3.5},{2,3},{2,-3},{-2,-3},{-2,3},{0,3},{0,5},{-10,5}}; tm3={{-10,-5},{10,-5},{10,5},{0,4.5},{1,3.5},{2,3},{2,-3},{-2,-3},{-2,3},{0,3},{0,5},{-10,5}}; tm4={{-10,-5},{10,-5},{10,5},{0,5},{0,3},{2,3},{2,-3},{-2,-3},{-2,3},{0,3},{0,5},{-10,5}}; tm5={{-10,-5},{10,-5},{10,4.5},{-0.75,4.5},{-0.75,3.5},{2,3.5},{2,-3},{-2,-3},{-2,3},{0.75,3},{0.75,5},{-10,5}}; tm6={{-10,-5},{10,-5},{10,7},{-9,4.5},{-9,3.5},{2,-2},{-2,-3},{-2,3},{9,3.5},{9,4.5},{-10,7}}; tm7={{-10,-5},{10,-5},{10,5},{.5,5},{-1,4},{.5,3},{-1,2},{.5,1},{-1,0},{.5,-1},{2,-1},{2,-3},{-2,-3},{-2,-1},{-.5,-1},{1,0},{-.5,1},{1,2},{-.5,3},{1,4},{-.5,5},{-10,5}}; tm8={{13876.088285207748`,13583.902501240373`},{13901.698801517487`,13628.228394724429`},{13919.968444108963`,13659.692779097706`},{13935.85636305809`,13687.496636971831`},{13963.85636305809`,13735.496636971831`},{13980.172897577286`,13764.05057232827`},{13998.918132781982`,13796.608086518943`},{14040.546700874964`,13868.696582235396`},{14060.004526236118`,13903.382270960472`},{14087.774329972268`,13945.03697647041`},{14106.99999988079`,14057.987787880003`},{14107.`,14051.3012342304`},{14051.902840881348`,13830.91259828031`},{13871.37843067944`,13861.`},{13874.793525728837`,13861.`},{14022.955277819834`,13838.205884293207`},{14115.38800375802`,13998.422609171696`},{14128.616750717163`,14021.82731544599`},{14159.856363117695`,14076.496637016535`},{14187.85636305809`,14124.496636971831`},{14203.167274781636`,14151.290732435882`},{13703.167274781636`,14151.290732435882`}}; tm9={{0,0},{2,0},{11,4},{-1,4},{8,1},{6,7},{7,0},{10,0},{10,6},{0,6}}; tm10={{0,0},{10,0},{10,6},{8,6},{-1,4},{7,2},{3,2},{11,4},{2,6},{0,6}}; tm11={{0,0},{2,0},{11,4},{-1,4},{4,0.5},{6,7},{7,0},{10,0},{10,6},{0,6}}; tms = {tm1, tm2, tm3, tm4, tm5, tm6, tm7, tm8, tm9, tm10, tm11};

First, we go along with @cvgmt go get the reg:

outerContour[points_]:=Module[{cb,reg,segs,fcs,mc,reg1,mc1,polys,segs1,tal}, cb=CoordinateBounds[points,.5]; reg=RegionDifference[BoundaryMesh[Rectangle@@Transpose@cb],Polygon@points];

Get rid of first four (those are from the rectangle), to get the intersected line segments:

segs=Drop[Sort@MeshCells[reg,1][[All,1]],4];

We turn these segments into an undirected graph; its FindFundamentalCycles give us a set of polygons which we can merge to get a non-intersecting polygon representation, which is then triangulated:

fcs=FindFundamentalCycles@Graph[UndirectedEdge@@@segs]; mc=MeshCoordinates@reg; reg1=DiscretizeGraphics@Graphics`PolygonUtils`PolygonUnion[Polygon@#&/@(mc[[#]]&/@fcs[[All,All,1]])]; mc1=MeshCoordinates@reg1; polys=MeshCells[reg1,2][[All,1]];

FInally, those triangles' segments are counted with Tally, so those that are only counted once, make up the boundary we are after:

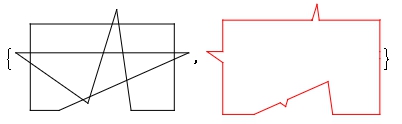
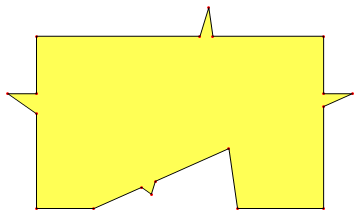
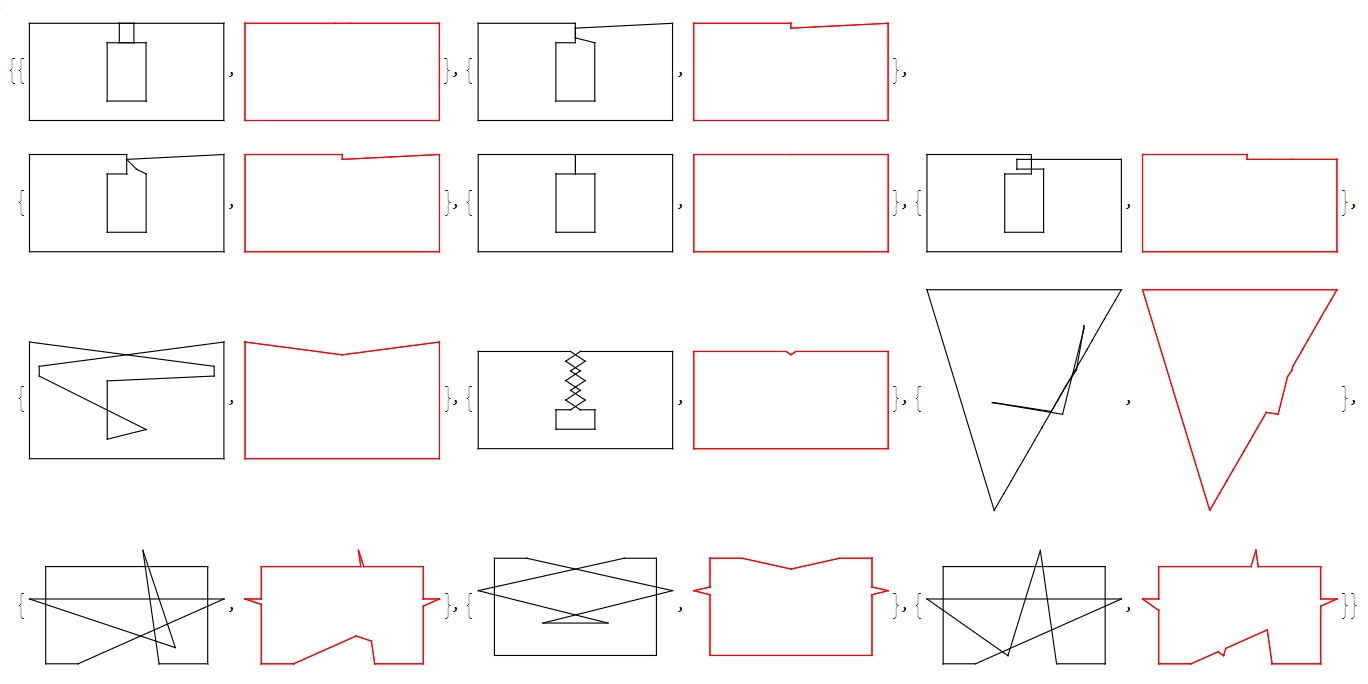
segs1=Sort/@Flatten[Transpose[{#,RotateLeft@#}]&/@polys,1]; Partition[mc1[[Flatten[Pick[tal=Tally@segs1;tal[[All,1]],tal[[All,2]],1],1]]],2] ]; {Graphics@{Thread@Line@Transpose[{#,RotateLeft@#}]},Graphics@{Red,Thread@Line@Transpose[{outerC=outerContour[#];outerC,RotateLeft@outerC}]}}&/@tms

FindFundamentalCycles seems to do the job, though it's not obvious why it always generates cycles that cover 100% of any Polygon@points. But it does, in all my toy model cases.

enter image description here

UPD.

Based on @azerbajdzan solution, a bit cleaner: 
contourPolygon1[x_] := Polygon[#[[1]][[FirstCase[#[[2]], _List, #[[2]], All]]]] &@ CrossingPolygon[x] Graphics[{EdgeForm[Black], Thread@Line@Transpose[{#, RotateLeft@#}], FaceForm[None], EdgeForm[{Red}], contourPolygon1[#]}] & /@ tms // Multicolumn[#] &

enter image description here

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.