2
$\begingroup$

I have an expression for the form

Subscript[W, f[a, b]][c] = ρ^f[a,b]ω[c]ρ^-f[a,b]

that I want to render in TraditionalForm for a variety of values a,b, and c so that, for example when c==7 and f[a,b]==5 for given b and c I get

$$W_5(7)=\rho^{5}\omega(7)\rho^{-5}$$

but I can't figure out how to get Mathematica to evaluate the parts I need evaluated, while leaving alone the parts I need left alone to get the desired result.

For example, 

TraditionalForm[Subscript[W, f[a, b]][c] = ρ^f[a,b]ω[c]ρ^-f[a,b]]

just results in

$$\omega(7)$$

How can I control evaluation and formatting of my expression to have the desired parts evaluated (here for example the application of f and the values of a,b, and c, without also collapsing the whole structure of the expression?

Improve this question
$\endgroup$

3 Answers 3

Reset to default
3
$\begingroup$ 
res = TraditionalForm[ HoldForm[Subscript[W, f[a, b]][ c] == \[Rho]^f[a, b] \[Omega][c] \[Rho]^-f[a, b]]]; res /. {c -> 7, f[a, b] -> 5};

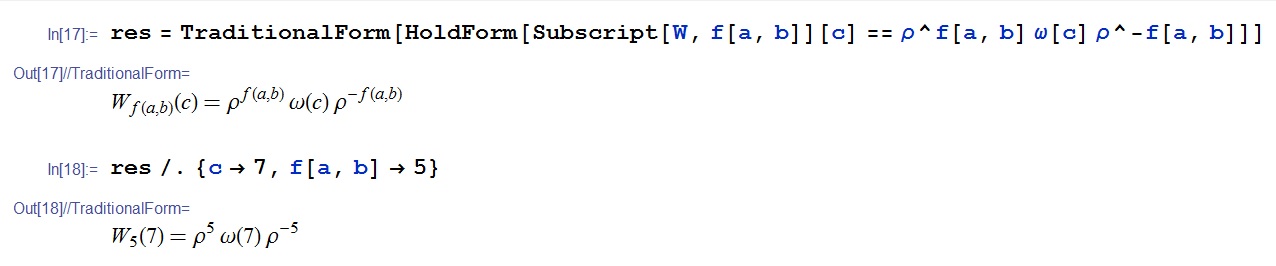
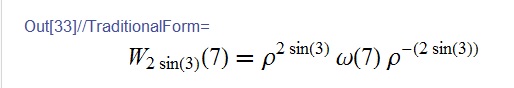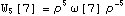enter image description here

For your second question you can try this:

g[a_,b_]:=a Sin[b]; res /. {c -> 7, f[a, b] -> g[2 , 3]}

enter image description here

Improve this answer
$\endgroup$
8
  • $\begingroup$ Excellent! What about when f is defined elsewhere; that is, I have f[a_,b_] := ... somewhere else and can vary; i.e the right hand side of the f[a,b] -> ... rule is not constant but depends on a and b? $\endgroup$ Commented Mar 7, 2015 at 23:39
  • 1
    $\begingroup$ @raxacoricofallapatorius please check the update. $\endgroup$ Commented Mar 7, 2015 at 23:44
  • $\begingroup$ Yes but a and b could be coming from anywhere. For example TraditionalForm[HoldForm[Subscript[W, f[#, b]][c] = ρ^f[#, b] ω[c] ρ^-f[#, b]]] & /@ Range[3] /. {b -> 2, c -> 7, f[a, b] -> g[a, b]} leaves all the f unsubstituted, while I need them replaced with the evaluation of g. $\endgroup$ Commented Mar 8, 2015 at 20:50
  • $\begingroup$ In this case use pattern replacement: TraditionalForm[ HoldForm[ Subscript[W, f[#, b]][ c] = [Rho]^f[#, b] [Omega][c] [Rho]^-f[#, b]]] & /@ Range[3] /. {b -> 2, c -> 7} /. {f[a_, b_] -> g[a, b]}. $\endgroup$ Commented Mar 8, 2015 at 21:29
  • $\begingroup$ That leaves g[a,b] unevaluated. For example if g[a, b] := a + b it leaves 1+2, etc. rather than 3; and if g[a, b] is more complex, it results in errors. $\endgroup$ Commented Mar 9, 2015 at 12:44
3
$\begingroup$

Crucial, for answer to this question, is: why parts of our expression should "stay unevaluated".

= in Mathematica is Set function. If we want to express assignment, but just don't want to evaluate it, then we can use = and HoldForm like in rasher's answer, or, if we just want to suppress Set evaluation, we can Inactivate it:

Inactivate[Subscript[W, f[a, b]][c] = ρ^f[a, b] ω[c] ρ^-f[a, b], Set] // TraditionalForm

$W_{f(a,b)}(c)=\omega (c)$

If later we want to perform this assignment we can take above expression and Activate it.

If we want to express equality, not assignment, then use == as already suggested by Algohi it renders the same in TraditonalForm, but there's no Set evaluation to suppress.

Subscript[W, f[a, b]][c] == ρ^f[a, b] ω[c] ρ^-f[a, b] // TraditionalForm

$W_{f(a,b)}(c)=\omega (c)$

There's still "unwanted evaluation" on right hand side. The question is similar: why we don't want ρ^f[a, b] ω[c] ρ^-f[a, b] to evaluate to ω[c].

If we want it to preserve exactly this form and prevent any evaluation, then we should use HoldForm, as in other answers.

If we just want to prevent simplifications of multiplication, then again we should ask ourselves why.

  • If this is an ordinary commuting multiplication, but we just don't want it to perform built-in simplifications, then we can inactivate Times function, for example like this:

    Subscript[W, f[a, b]][c] == Inactive[Times][ρ^f[a, b], ω[c], ρ^-f[a, b]] // TraditionalForm

    $W_{f(a,b)}(c)=\rho ^{f(a,b)}*\omega (c)*\rho ^{-f(a,b)}$

    If we don't want * signs, we can change TraditionalForm boxes of Inactive[Times] to be the same as of ordinary Times:

    MakeBoxes[Inactive[Times][x__], TraditionalForm] := MakeBoxes[HoldForm@Times[x], TraditionalForm] Subscript[W, f[a, b]][c] == Inactive[Times][ρ^f[a, b], ω[c], ρ^-f[a, b]] // TraditionalForm

    $W_{f(a,b)}(c)=\rho ^{f(a,b)}\omega (c)\rho ^{-f(a,b)}$

    As in case of inactive Set, we can at any point Activate Times.

  • If ρ and ω don't commute, then use ** instead of Times.

    Subscript[W, f[a, b]][c] == ρ^f[a, b] ** ω[c] ** ρ^-f[a, b] // TraditionalForm

    $W_{f(a,b)}(c)=\rho ^{f(a,b)}\text{**}\omega (c)\text{**}\rho ^{-f(a,b)}$

    Again if we don't want stars, we can change TraditionalForm boxes of NonCommutativeMultiply to be the same as of ordinary Times:

    MakeBoxes[NonCommutativeMultiply[x__], TraditionalForm] := MakeBoxes[HoldForm@Times[x], TraditionalForm] Subscript[W, f[a, b]][c] == ρ^f[a, b] ** ω[c] ** ρ^-f[a, b] // TraditionalForm

    $W_{f(a,b)}(c)=\rho ^{f(a,b)}\omega (c)\rho ^{-f(a,b)}$

Negative powers

In Mathematica expressions with with negative numeric powers are rendered as division by same expressions with positive power:

a^-5

$\frac{1}{a^5}$

As we can see in FullForm:

a^-5 //FullForm (* Power[a,-5] *)

This is still Power expression, so no simplifications where performed. Result we're getting is done when expression is converted to boxes and holding evaluation will not help here.

HoldForm[a^-5]

$\frac{1}{a^5}$

It may seem to work when we do something like:

HoldForm[a^-b] /. b -> 5

$a^{-5}$

But what really happens is that we have held multiplication of -1 and 5 which can be seen in FullForm:

HoldForm[a^-b] /. b -> 5 // FullForm (* HoldForm[Power[a,Times[-1,5]]] *)

Above expression is rendered as we want because exponent is not a negative number. It is a more complicated expression. This expression would evaluate to negative number, but we've prevented its evaluation. Here we see also another feature: multiplication by -1 has also some special rendering rules.

That's why holding evaluation will fail e.g. in this situation:

HoldForm[a^-b] /. b -> -5

$a^{-(-5)}$

If we want to get different boxes for Power expressions, instead of holding evaluation, we need to define special box representations.

Going back to example from question. Power[ρ, ...] in TraditionalForm is rendered, as power of any other symbol:

ρ^5 // TraditionalForm

$\rho^5$

ρ^(1/2) // TraditionalForm

$\sqrt{\rho}$

ρ^-5 // TraditionalForm

$\frac{1}{\rho^5}$

ρ^-a // TraditionalForm

$\rho^{-a}$

To change this behavior we need to redefine TraditionalForm boxes for such expressions, for example like this:

MakeBoxes[HoldPattern@Power[ρ, x_], TraditionalForm] := SuperscriptBox["ρ", MakeBoxes[x, TraditionalForm]]

Now we get:

ρ^5 // TraditionalForm

$\rho^5$

ρ^(1/2) // TraditionalForm

$\rho^{\frac{1}{2}}$

ρ^-5 // TraditionalForm

$\rho^{-5}$

ρ^-a // TraditionalForm

$\rho^{-a}$

Summary

With special formatting defined e.g. like this:

MakeBoxes[HoldPattern@Power[ρ, x_], TraditionalForm] := SuperscriptBox["ρ", MakeBoxes[x, TraditionalForm]] MakeBoxes[HoldPattern@NonCommutativeMultiply[x__], TraditionalForm] := RowBox[List @@ (Function[expr, MakeBoxes[expr, TraditionalForm], HoldAllComplete] /@ HoldComplete[x])]

we get:

Subscript[W, f[a, b]][c] == ρ^f[a, b] ** ω[c] ** ρ^-f[a, b] // TraditionalForm % /. {f[a, b] -> 5, c -> 7} // TraditionalForm

$W_{f(a,b)}(c)=\rho ^{f(a,b)}\omega (c)\rho ^{-f(a,b)}$

$W_5(7)=\rho^5\omega(7)\rho^{-5}$

without any evaluation manipulations.

Improve this answer
$\endgroup$
2
$\begingroup$ 
ls = HoldForm[Subscript[W, f[a, b]][c] = ρ^f[a, b] ω[c] ρ^-f[a, b]] ReplaceRepeated[ls, {f[a, b] -> 5, c -> 7}]

enter image description here

Then just TraditionalForm that...

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.