How can I draw the figure shown above in rectangular coordinates, calculate the area and perimeter of the shaded region as a function of radius r of the outer circle, and find the points of intersection of the inner circles.
$\begingroup$ $\endgroup$
7 
5 Answers
$\begingroup$ $\endgroup$
2 Show it:
RegionPlot[ region = RegionUnion[ Sequence @@ RegionIntersection @@@ Subsets[{Disk[{-1, 0}], Disk[{0, -1}], Disk[{1, 0}], Disk[{0, 1}]}, {2}], Fold[RegionDifference, {Disk[{0, 0}, 2], Disk[{-1, 0}], Disk[{0, -1}], Disk[{1, 0}], Disk[{0, 1}]}]], Frame -> False]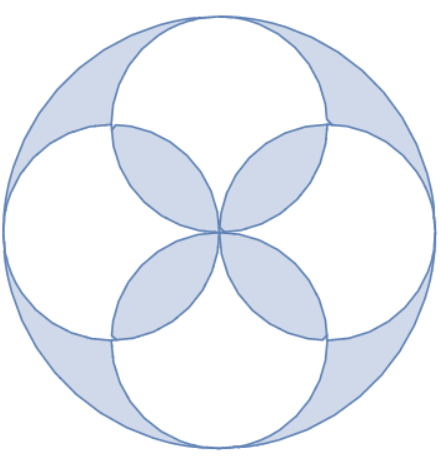 
Area
Area[region] 4 (-2 + π)
Perimeter
ArcLength@RegionBoundary[region] 12 π
- $\begingroup$ why does the code show that weird angle at the intersection points? $\endgroup$Alucard– Alucard2017-02-21 04:14:42 +00:00Commented Feb 21, 2017 at 4:14
- $\begingroup$ @Alucard: Plotting functions have finite accuracy. This can be fixed by adding the MaxRecursion -> 5 option to RegionPlot (perhaps there are better ways). $\endgroup$Meni Rosenfeld– Meni Rosenfeld2017-02-21 11:01:17 +00:00Commented Feb 21, 2017 at 11:01
$\begingroup$ $\endgroup$
2 I would use BooleanRegion:
reg = BooleanRegion[ Xor, {Disk[{-1,0},1], Disk[{0,1},1], Disk[{1,0},1], Disk[{0,-1},1], Disk[{0,0},2]} ]; RegionMeasure @ reg RegionMeasure @ RegionBoundary @ reg 4 (-2 + Pi)
12 Pi
- $\begingroup$ Thank you all, now I have a clearer idea of doing this with more difficult figures $\endgroup$zeros– zeros2017-03-03 19:57:40 +00:00Commented Mar 3, 2017 at 19:57
- $\begingroup$ BTW, instead of
RegionMeasureandRegionMeasure@*RegionBoundaryone can useArea, and in v11.1,Perimeter. $\endgroup$kirma– kirma2017-03-19 14:02:58 +00:00Commented Mar 19, 2017 at 14:02
$\begingroup$ $\endgroup$
Your question wants a relationship for r which I assume is the radius of the larger circle. You can get it like this:
c1 = ImplicitRegion[(x - r)^2 + y^2 <= r^2, {x, y}]; c2 = ImplicitRegion[x^2 + (y - r)^2 <= r^2, {x, y}]; Assuming[r > 0, Area[RegionIntersection[c1, c2]]] yields
$\frac{1}{2} (\pi -2) r^2$
All the shaded areas in terms of r:
FullSimplify[\[Pi]*r^2 - 4 \[Pi] (r/2)^2 + 8 1/8 (-2 + \[Pi]) r^2] $\left ( \pi -2\right )r^2$
Testing for the particular answer given by yode:
(-2 + \[Pi]) r^2 /. r -> 2 yields
$4\pi - 8$
$\begingroup$ $\endgroup$
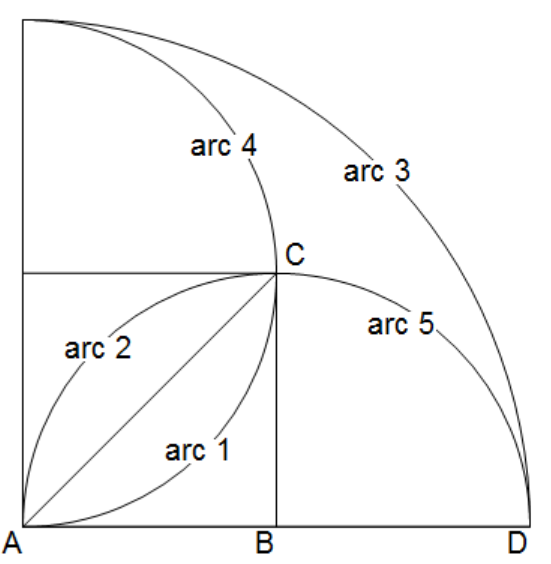
1 Just for fun. By symmetry we need only consider the first quadrant.
Graphics[{EdgeForm[Black], FaceForm[None], Disk[{0, 0}, 2, {0, Pi/2}], Disk[{1, 0}, 1, {0, Pi}], Disk[{0, 1}, 1, {-Pi/2, Pi/2}], Line[{{1, 0}, {1, 1}}], Line[{{0, 0}, {1, 1}}], Line[{{0, 1}, {1, 1}}], Text[Style["A", 20], {0, 0}, {1, 1}], Text[Style["B", 20], {1, 0}, {1, 1}], Text[Style["C", 20], {1, 1}, {-2, -1}], Text[Style["D", 20], {2, 0}, {1, 1}], Text[Style["arc 1", 20, Background -> White], {0.7, 0.3}, {0, 0}], Text[Style["arc 2", 20, Background -> White], {0.3, 0.7}, {0, 0}], Text[Style["arc 3", 20, Background -> White], {1.4, 1.4}, {0, 0}], Text[Style["arc 4", 20, Background -> White], {0.8, 1.5}, {0, 0}], Text[Style["arc 5", 20, Background -> White], {1.5, 0.8}, {0, 0}] }] 
Let the radius of the small circle be 1 (hence the radius of the large circle is 2).
So the perimeter can be seen to be length of arc1+ arc2+arc3+arc4+arc5:
Let $p_i$ represent arc i length. Now $p_1=p_2=p_4=p_5= \pi/2$ and arc length $p3= \pi/2 \times 2$. Hence total perimeter:
perimeter = 4 (4 Pi/2 + Pi/2 2) i.e. $12\pi$
For the area: area bounded by arc1 and arc 2 is 2 x (area of sector-area of triangle ABC):
area1 = 2 (Pi/4 - 1/2) The area bounded by arcs 3,4 and 5= area of quarter circle -area of 2 semicircles+ area of overlap:
area2 = (Pi/2) 2^2/2 - Pi + area1 Note area1=area2=$\pi/2-1$, so the total area is
total = Simplify[4 (area1 + area2)] yielding:
4 (-2 + \[Pi]) 
- $\begingroup$ Thank you all, now I have a clearer idea of doing this with more difficult figures $\endgroup$zeros– zeros2017-03-03 19:57:56 +00:00Commented Mar 3, 2017 at 19:57
$\begingroup$ $\endgroup$
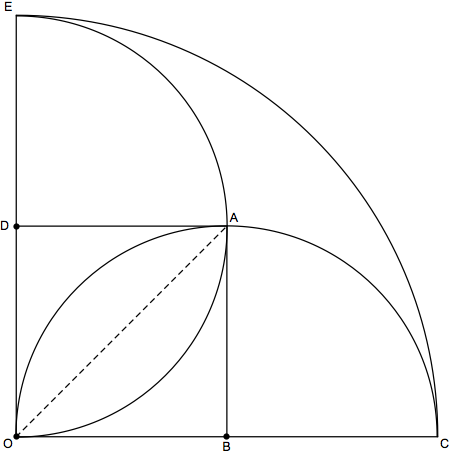
1 This isn't really a Mathematica problem. It is a Euclidean geometry problem and can be solve by a little classic geometry reasoning. Like ubpdqn I will work in the 1st quadrant and invoke symmetry.
By construction
$\qquad$OC = OE = R
$\qquad$OB = OD = DA = BA = R/2
By observation
$\qquad$Quadrant perimeter = EA + AO + OA + BA + EC
$\qquad$OBAD is a square
Arcs EA + OA and AO, + BA are one half the circumference of the equal circles centered at B and D, which have diameters R/2, so EA + OA + AO, + BA = circumference of an inner circle = π R. EC is one quarter of the circumference of the outer circle, so EC = (2 π R)/4 = π R/2. The quadrant perimeter is therefore π R + π R/2 = 3 π R/2.
It follows that the full perimeter, 4 x (quadrant perimeter), is 6 π R.
Point A is one of the points where the inner circles intersect and it clearly lies at {R/2, R/2}. By symmetry, the four points of intersection are
$\qquad${{R/2, R/2}, {-R/2, R/2}, {-R/2, -R/2}, {R/2, -R/2}}.
Finding the area is a little more complicated, but not much.
The area, a1, between the two arcs ending at points O and A is clearly twice the difference of the area between the arc OA and the dashed line OA. This in turn is the area of a quadrant of inner circle centered at B less the half the square OBAD. Thus,
$\qquad$a1 = 2 ((π (R/2)^2)/4 - ((R/2)^2)/2) = 1/8 (π - 2) R^2
The area, a2, bordered by the arcs EC, EA and AC is the area of the quadrant less the area of 2 quadrants of an inner circle less the area of the square OBAD. This is given by
$\qquad$a2 = (π R^2)/4 - (π (R/2)^2)/2 - (R/2)^2 = 1/8 (π - 2) R^2
Note that a1 = a2 (which I find an interesting result in itself). Therefore, the full area is
$\qquad$4 (2 a1) = (π - 2) R^2
- $\begingroup$ Thank you all, now I have a clearer idea of doing this with more difficult figures $\endgroup$zeros– zeros2017-03-03 19:57:25 +00:00Commented Mar 3, 2017 at 19:57
code-requestbecause any other interpretation imo would render this question as posted on the wrong site. $\endgroup$