0
$\begingroup$

I consider the following function:

bound[K10_] := xi - (p0*(Q10 - K10)/(p0 - K10 + Sqrt[(K10)^2 - m1^2]*(1 - 2*alpha)))/(u0Max);

This function is basically an implicit function which relates the variable xi to alpha. p0,Q10,m1 and u0Max are constants, which i set to

p0 = 1; m1 = 0.1; m2 = 0.1; Q10 = 1/2*(p0 + (m1 - m2)*(m1 + m2)/p0); Q10Min = (m1^2 + p0^2/4)/p0; u0Max = p0*(Q10 - Q10Min)/(p0 - Q10Min - Sqrt[Q10Min^2 - m1^2]);

K10P is defined in the following way:

K10P = -m1^2*Q10*(1 - 2*alpha)^2/(p0^2 - 2*p0*Q10 + Q10^2*(1 - (1 - 2*alpha)^2)) + Sqrt[(-m1^2*Q10*(1 - 2*alpha)^2/(p0^2 - 2*p0*Q10 + Q10^2*(1 - (1 - 2*alpha)^2)))^2 + (m1^4*(1 - 2*alpha)^2 + m1^2*(p0 - Q10)^2)/(p0^2 - 2*p0*Q10 + Q10^2*(1 - (1 - 2*alpha)^2))];

The implicit function "bound[K10_]" defines a function of the form xi[alpha], but i would like to solve this implicit function for alpha and obtain an expression depending on xi only, so i try:

Solve[bound[K10P] == 0, alpha];

Unfortunately, this does not work in the sense that this command runs forever without solving the equation. Do you have any suggestions how to obtain my desired expression?

Improve this question
$\endgroup$

2 Answers 2

Reset to default
7
$\begingroup$

Could turn it into a polynomial relation using GroebnerBasis.

bound[K10_] := xi - (p0*(Q10 - K10)/(p0 - K10 + Sqrt[(K10)^2 - m1^2]*(1 - 2*alpha)))/(u0Max); p0 = 1; m1 = 1/10; m2 = 1/10; Q10 = 1/2*(p0 + (m1 - m2)*(m1 + m2)/p0); Q10Min = (m1^2 + p0^2/4)/p0; u0Max = p0*(Q10 - Q10Min)/(p0 - Q10Min - Sqrt[Q10Min^2 - m1^2]); K10P = -m1^2* Q10*(1 - 2*alpha)^2/(p0^2 - 2*p0*Q10 + Q10^2*(1 - (1 - 2*alpha)^2)) + Sqrt[(-m1^2* Q10*(1 - 2*alpha)^2/(p0^2 - 2*p0*Q10 + Q10^2*(1 - (1 - 2*alpha)^2)))^2 + (m1^4*(1 - 2*alpha)^2 + m1^2*(p0 - Q10)^2)/(p0^2 - 2*p0*Q10 + Q10^2*(1 - (1 - 2*alpha)^2))]; gb = GroebnerBasis[bound[K10P], {alpha, xi}]; alphaxi = First[gb] (* Out[43]= -390625 - 37500000 alpha + 37500000 alpha^2 + 1531250 xi + 147000000 alpha xi - 147000000 alpha^2 xi - 1875625 xi^2 - 217530000 alpha xi^2 + 220410000 alpha^2 xi^2 - 5760000 alpha^3 xi^2 + 2880000 alpha^4 xi^2 + 735000 xi^3 + 144001200 alpha xi^3 - 149646000 alpha^2 xi^3 + 11289600 alpha^3 xi^3 - 5644800 alpha^4 xi^3 - 35985600 alpha xi^4 + 38807424 alpha^2 xi^4 - 5698944 alpha^3 xi^4 + 2987712 alpha^4 xi^4 - 165888 alpha^5 xi^4 + 55296 alpha^6 xi^4 *)

It turns out that this factors into a quadratic and a quartic in alpha, so if so desired one can get radical solution branches.

Factor[alphaxi] (* Out[47]= (625 - 1225 xi + 600 xi^2 - 24 alpha xi^2 + 24 alpha^2 xi^2) (-625 - 60000 alpha + 60000 alpha^2 + 1225 xi + 117600 alpha xi - 117600 alpha^2 xi - 59976 alpha xi^2 + 62280 alpha^2 xi^2 - 4608 alpha^3 xi^2 + 2304 alpha^4 xi^2) *)
Improve this answer
$\endgroup$
3
  • $\begingroup$ This works well, thanks for the suggestion. Is it also possible to extend this method such that i can use arbitrary values for p0,m1 and m2? $\endgroup$ Commented Jul 4, 2019 at 13:42
  • $\begingroup$ You can try that. I think it should work in the same way. $\endgroup$ Commented Jul 4, 2019 at 15:32
  • $\begingroup$ It works for sure if i replace the values for p0,m1 or m2 by different values, but i am looking for a final expression which depends on p0,m1 and m2 and can be chosen arbitrarily. If i try this, it does not work. $\endgroup$ Commented Jul 4, 2019 at 15:45
2
$\begingroup$

First, let's build the function you want to define. We use your equation bound[K10P] == 0 and more general Re[bound[K10P]] == 0

Q10 = 1/2*(p0 + (m1 - m2)*(m1 + m2)/p0); Q10Min = (m1^2 + p0^2/4)/p0; u0Max = p0*(Q10 - Q10Min)/(p0 - Q10Min - Sqrt[Q10Min^2 - m1^2]); K10P = -m1^2* Q10*(1 - 2*alpha)^2/(p0^2 - 2*p0*Q10 + Q10^2*(1 - (1 - 2*alpha)^2)) + Sqrt[(-m1^2* Q10*(1 - 2*alpha)^2/(p0^2 - 2*p0*Q10 + Q10^2*(1 - (1 - 2*alpha)^2)))^2 + (m1^4*(1 - 2*alpha)^2 + m1^2*(p0 - Q10)^2)/(p0^2 - 2*p0*Q10 + Q10^2*(1 - (1 - 2*alpha)^2))]; ContourPlot[bound[K10P] == 0, {alpha, -1, 2}, {xi, 0, 1.2}, FrameLabel -> Automatic, PlotPoints -> 150] ContourPlot[Re[bound[K10P]] == 0, {alpha, -5, 5}, {xi, 0, 1.2}, FrameLabel -> Automatic, PlotPoints -> 150]

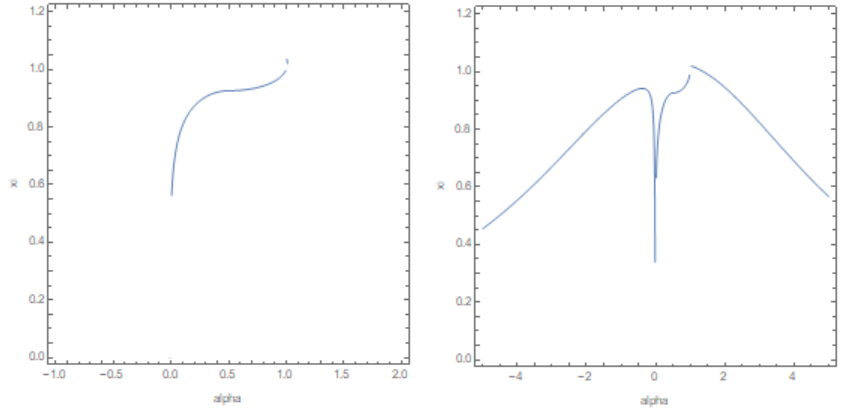
Figure 1

We see that the alpha function has several branches for real values of xi. This is the problem. The same can be obtained using

bound[K10P] // FullSimplify Out[]= -((25 (96 - Sqrt[( 1 - 96 (-1 + alpha) alpha)/((-1 + alpha)^2 alpha^2)] + 1/( alpha - alpha^2)))/(12 (196 + 1/(1 - alpha) + 1/alpha - Sqrt[( 1 - 96 (-1 + alpha) alpha)/((-1 + alpha)^2 alpha^2)] + Sqrt[2] (1 - 2 alpha) Sqrt[((1 - 2 alpha)^2 (1 + (-1 + alpha) alpha (-48 + Sqrt[( 1 - 96 (-1 + alpha) alpha)/((-1 + alpha)^2 alpha^2)])))/((-1 + alpha)^2 alpha^2)]))) + xi

From here we immediately find (xif=xi)

xif[alpha_] := ( 25 (96 - Sqrt[( 1 - 96 (-1 + alpha) alpha)/((-1 + alpha)^2 alpha^2)] + 1/( alpha - alpha^2)))/( 12 (196 + 1/(1 - alpha) + 1/alpha - Sqrt[( 1 - 96 (-1 + alpha) alpha)/((-1 + alpha)^2 alpha^2)] + Sqrt[2] (1 - 2 alpha) Sqrt[((1 - 2 alpha)^2 (1 + (-1 + alpha) alpha (-48 + Sqrt[( 1 - 96 (-1 + alpha) alpha)/((-1 + alpha)^2 alpha^2)])))/((-1 + alpha)^2 alpha^2)]))

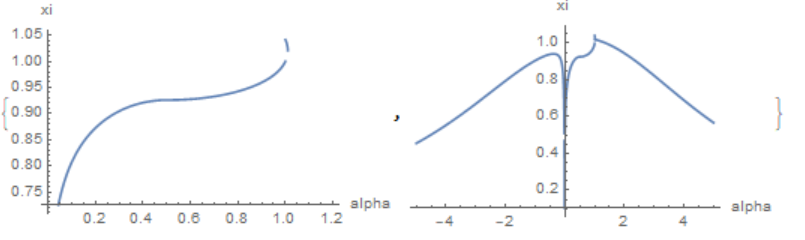
Get the same curves

{Plot[xif[x], {x, 0, 1.2}, PlotPoints -> 200, AxesLabel -> {"alpha", "xi"}], Plot[Re[xif[x]], {x, -5, 5}, PlotPoints -> 200, AxesLabel -> {"alpha", "xi"}]}

Figure2

Define the inverse function

\[Alpha] = InverseFunction[ Function[{alpha}, ( 25 (96 - Sqrt[( 1 - 96 (-1 + alpha) alpha)/((-1 + alpha)^2 alpha^2)] + 1/( alpha - alpha^2)))/( 12 (196 + 1/(1 - alpha) + 1/alpha - Sqrt[( 1 - 96 (-1 + alpha) alpha)/((-1 + alpha)^2 alpha^2)] + Sqrt[2] (1 - 2 alpha) Sqrt[((1 - 2 alpha)^2 (1 + (-1 + alpha) alpha (-48 + Sqrt[( 1 - 96 (-1 + alpha) alpha)/((-1 + alpha)^2 alpha^2)])))/((-1 + alpha)^2 alpha^2)]))]]

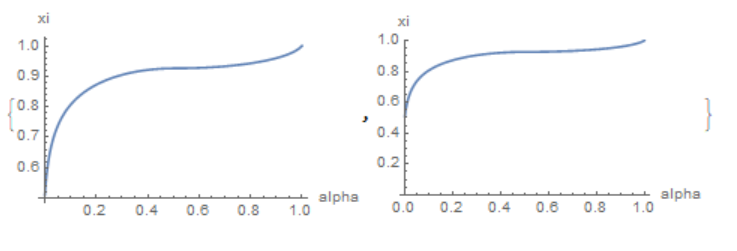
If you evaluate the alpha function, then there will be no answer, since the system will not be able to select a branch. But you can choose the branch of the solution of the equation. Suppose we chose branch 0<alpha<1. Define the function

xif[alpha_ /; alpha > 0 && alpha < 1] := ( 25 (96 - Sqrt[( 1 - 96 (-1 + alpha) alpha)/((-1 + alpha)^2 alpha^2)] + 1/( alpha - alpha^2)))/( 12 (196 + 1/(1 - alpha) + 1/alpha - Sqrt[( 1 - 96 (-1 + alpha) alpha)/((-1 + alpha)^2 alpha^2)] + Sqrt[2] (1 - 2 alpha) Sqrt[((1 - 2 alpha)^2 (1 + (-1 + alpha) alpha (-48 + Sqrt[( 1 - 96 (-1 + alpha) alpha)/((-1 + alpha)^2 alpha^2)])))/((-1 + alpha)^2 alpha^2)]))

Make sure that we select the desired branch:

{Plot[xif[x], {x, 0, 1.2}, PlotPoints -> 200, AxesLabel -> {"alpha", "xi"}, PlotRange -> All], Plot[Re[xif[x]], {x, -5, 5}, PlotPoints -> 200, AxesLabel -> {"alpha", "xi"}, PlotRange -> {0, 1}]}

Figure 3

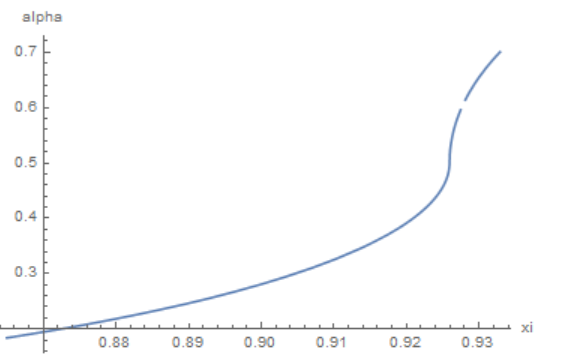
Define and plot the inverse function

alph = InverseFunction[xif] Plot[alph[x], {x, .3, 0.99}, PlotRange -> All, AxesLabel -> {"xi", "alpha"}]

Figure 4

Improve this answer
$\endgroup$
3
  • $\begingroup$ How can i choose the branch in particular? Lets suppose that alpha is between 0 and 1 as you already plotted above. $\endgroup$ Commented Jul 3, 2019 at 20:23
  • $\begingroup$ @RealDestructor See update to my answer . $\endgroup$ Commented Jul 4, 2019 at 3:40
  • $\begingroup$ This works perfectly fine, thanks for that. Is it also possible to obtain an explicit analytical expression for the inverse function? $\endgroup$ Commented Jul 4, 2019 at 8:17

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.