1
$\begingroup$

I am trying to solve the following equation numerically.

NSolve[1/4 == 1/((3 + a) (a + 1)) + a^2/((3 a + 1) (a + 1)) + 1/((3 + a) (a + 1)) 1/4 (-1 + Sqrt[-1 - 2 a (1 + a) g12^2]) + a^2/((3 a + 1) (a + 1)) 1/4 (-1 + Sqrt[-1 - (2 (a + 1) )/a^2 g12^2]),a]

Where g12 is just a constant. Mathematica gives the solution in terms of Root[...] terms like

a -> Root[ 1. + (10. - 4. g12^2) #1 + (65. - 8. g12^2 + 4. g12^4) #1^2 + (224. - 32. g12^2 - 24. g12^4) #1^3 + (510. - 1016. g12^2 + 60. g12^4) #1^4 + (428. - 1976. g12^2 - 80. g12^4) #1^5 + (510. - 1016. g12^2 + 60. g12^4) #1^6 + (224. - 32. g12^2 - 24. g12^4) #1^7 + (65. - 8. g12^2 + 4. g12^4) #1^8 + (10. - 4. g12^2) #1^9 + #1^10 &, 1]

And I don't know how to deal with such a term. I have tried solving the equation in Root directly or stuff like N[Root[...]], but nothing works, and the term stays unchanged. How can I get an actual tangible result out of that equation?

Improve this question
$\endgroup$
2
  • 2
    $\begingroup$ Where g12 is just a constant it works for me on V 13.3.1 screen shot !Mathematica graphics did you set g12 to the constant you had? $\endgroup$ Commented Dec 23, 2023 at 23:57
  • 2
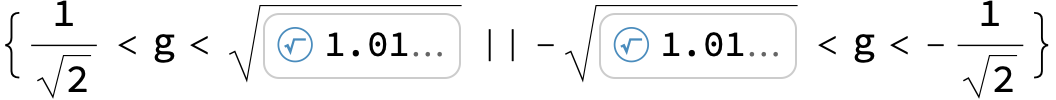
    $\begingroup$ I have tried solving the equation in Root directly or stuff like N[Root[...]] that will not work if your g12 does not have numerical value. Try setting g12 to numerical value first, it should work then. $\endgroup$ Commented Dec 24, 2023 at 0:10

1 Answer 1

Reset to default
3
$\begingroup$ 
$Version (* "13.3.1 for Mac OS X ARM (64-bit) (July 24, 2023)" *) Clear["Global`*"] eqn = 1/4 == 1/((3 + a) (a + 1)) + a^2/((3 a + 1) (a + 1)) + 1/((3 + a) (a + 1)) 1/4 (-1 + Sqrt[-1 - 2 a (1 + a) g12^2]) + a^2/((3 a + 1) (a + 1)) 1/4 (-1 + Sqrt[-1 - (2 (a + 1))/a^2 g12^2]);

Using Solve for the exact solutions

(sol = Solve[eqn, a]) // Short[#, 3] &

enter image description here

For the Root expressions to return a numeric value, g12 must have a numeric value.

For example, for g12 == 3

eqn /. sol /. g12 -> 3 // RootReduce (* {False, False, True, True, False, False, False, False, False, False} *)

As indicated in the warning message, not all solutions are valid for all values of the parameter g12

Selecting the two valid solutions for g12 == 3,

Pick @@ ({sol, eqn /. sol} /. g12 -> 3 // RootReduce) // N (* {{a -> -0.486416 - 0.873728 I}, {a -> -0.486416 + 0.873728 I}} *)

EDIT: For purely imaginary g12 and real a

eqn2 = eqn /. g12 -> I*g // Simplify (* ((a^2 (3 + Sqrt[-1 + (2 g^2)/a^2 + (2 g^2)/a]))/(1 + 3 a) + ( 3 + Sqrt[-1 + 2 a g^2 + 2 a^2 g^2])/(3 + a))/(4 (1 + a)) == 1/4 *) (sol2 = Solve[{eqn2, {a, g} ∈ Reals}, a]) // Short

enter image description here

DeleteDuplicates[a /. sol2 /. ConditionalExpression[e_, cond_] :> cond]

enter image description here

Plot[Evaluate[a /. sol2], {g, -1.1, 1.1}, AxesLabel -> (Style[#, 14] & /@ {Im[Subscript[g, 12]], a})]

enter image description here

Improve this answer
$\endgroup$
3
  • $\begingroup$ Would it be posible to insert an imaginary value for g12? Because from the analytical calculations I have done I expect g12 to be purely imaginary and alpha purely real. $\endgroup$ Commented Dec 24, 2023 at 0:58
  • $\begingroup$ Or more generally, would there be a way to check for which values of g12 (if any) a stays real? $\endgroup$ Commented Dec 24, 2023 at 1:08
  • 1
    $\begingroup$ I think maybe this is the question you wanted to ask? It’s certainly reasonable. But very different from what was actually asked. $\endgroup$ Commented Dec 24, 2023 at 2:26

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.