39
$\begingroup$

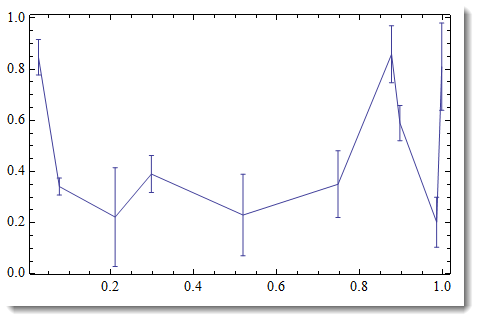
I have a plot with ErrorListPlot

data = Sort@RandomReal[1, {10, 2}]; error = RandomReal[0.5, 10]; errorplot = ErrorListPlot[ Partition[Riffle[data, ErrorBar /@ error], 2], Joined -> True]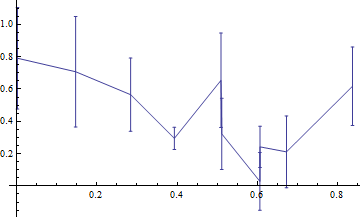

Mathematica graphics

However, I would like to have it with the y-axis on a log scale. I can use ListLogPlot to get the log scale but this doesn't plot the errorbars. 

logplot = ListLogPlot[ data, PlotRange -> All, AxesOrigin -> {0, 0}, Joined -> True ]

Mathematica graphics

I tried Show[logplot, errorplot, PlotRange->All] to see if it would plot with the scale and ticks from the logplot but that didn't work right:

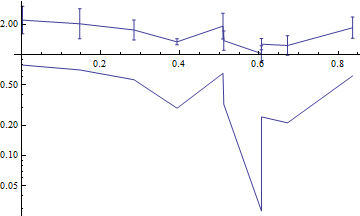
Mathematica graphics

I also tried to take the Ticks from the logplot: Show[errorplot, Ticks -> Ticks /. AbsoluteOptions@logplot] but that just gives an error.

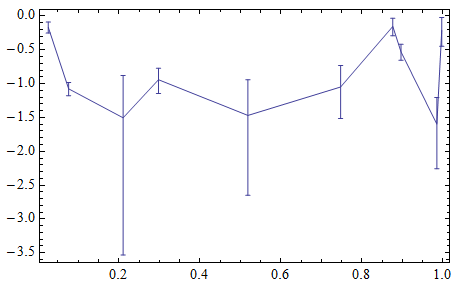
I tried to manually take the log of the data and then grab the tick-marks but that didn't work right

data = Sort@RandomReal[{10, 100}, {10, 2}]; error = RandomReal[20, 10]; logdata = Transpose[{data[[All, 1]], Log[10, data[[All, 2]]]}]; errorup = Log[10, data[[All, 2]] + error] - logdata[[All, 2]]; errordown = Log[10, data[[All, 2]] - error] - logdata[[All, 2]]; logerror = Log[10, error]; logplot = ListLogPlot[ data, Joined -> True, AxesOrigin -> {0, 0} ] errorlogplot = ErrorListPlot[ Partition[ Riffle[logdata, ErrorBar /@ Transpose[{errordown, errorup}]], 2], Joined -> True, AxesOrigin -> {0, 0} ] errorlogplot2 = ErrorListPlot[ Partition[ Riffle[logdata, ErrorBar /@ Transpose[{errordown, errorup}]], 2], Joined -> True, AxesOrigin -> {0, 0}, Ticks -> (Ticks /. AbsoluteOptions@logplot) ]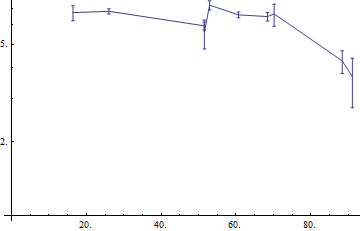

Mathematica graphics

Is there an easy way to do this?

On the log scale the error bars will appear asymmetrical.

Improve this question
$\endgroup$
4
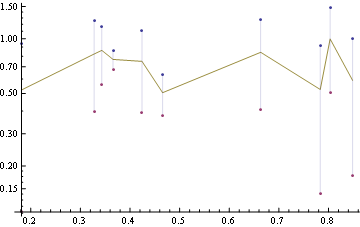
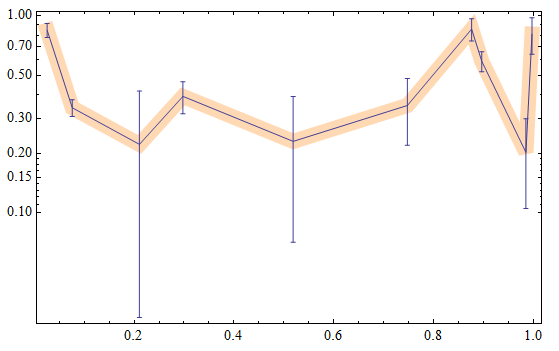
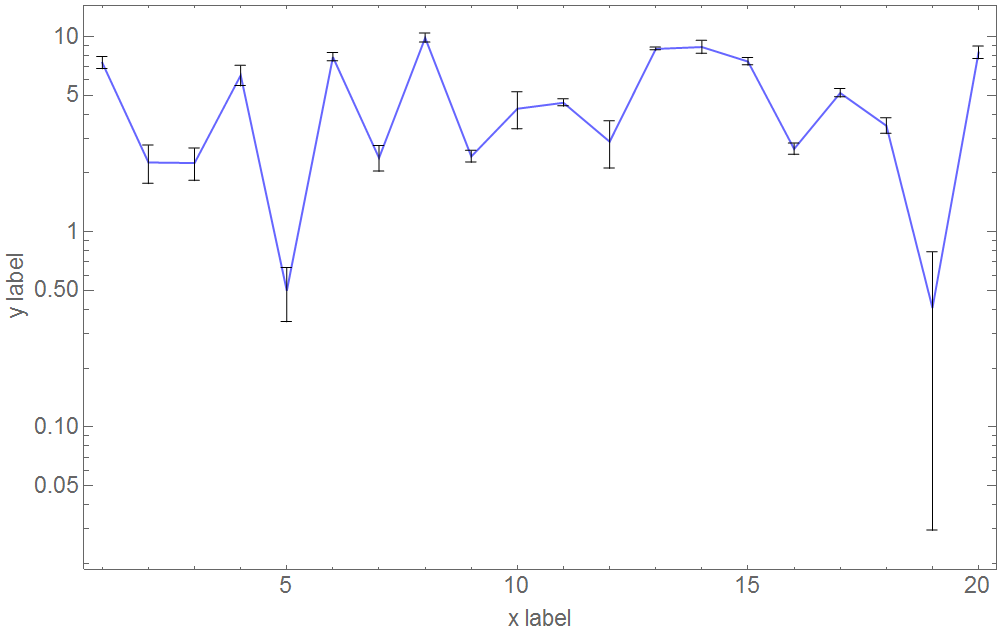
  • $\begingroup$ Have you tried LevelScheme? It's CustomTicks package is a superior alternative to trying to set it up by hand. The edition I have installed isn't functioning correctly, otherwise I would have posted it as an answer. But, it is worth a look. $\endgroup$ Commented Apr 4, 2012 at 3:58
  • 2
    $\begingroup$ Do you realize that 2 of your error bars on 1st plot have negative y-values? I guess it is an accident of making up a random data set, yet we should be aware of these logs of negative values. $\endgroup$ Commented Apr 4, 2012 at 7:53
  • 1
    $\begingroup$ @Vitaliy Kaurov, I realized that after I played with my random data more. I was originally working with a real dataset but it was simpler to post a line to generate random data then upload and link to the real data, however, my random data was slightly broken as you noticed. $\endgroup$ Commented Apr 4, 2012 at 19:30
  • $\begingroup$ Unfortunately horizontal error bars are not discussed. $\endgroup$ Commented Mar 22, 2017 at 12:10

5 Answers 5

Reset to default
20
$\begingroup$

I always use the package ErrorBarLogPlots. From the website:

ErrorBarLogPlots.m is a package which adds log-scale plotting functions similar to the standard ErrorListPlot provided in Mathematica 6. The added functions are ErrorListLogPlot, ErrorListLogLinearPlot, and ErrorListLogLogPlot."

Improve this answer
$\endgroup$
6
  • $\begingroup$ Strange...Once I write: Needs["ErrorBarLogPlots.m´"], I get the following error: Needs::cxt: Invalid context specified at position 1 in Needs[ErrorBarLogPlots.m\.b4]. A context must consist of valid symbol names separated by and ending with `. >> ... Am I doing something wrong? $\endgroup$ Commented Nov 30, 2012 at 13:35
  • $\begingroup$ @AnastasiiaAnishchenko Just write Needs["ErrorBarLogPlots`"]. $\endgroup$ Commented Nov 30, 2012 at 17:58
  • $\begingroup$ this doesn't work either...does one have to install anything in addition? I get this message: Needs::nocont: Context ErrorBarLogPlots` was not created when Needs was evaluated. >> $\endgroup$ Commented Dec 3, 2012 at 14:21
  • $\begingroup$ @AnastasiiaAnishchenko Hmm, I don't get this error. Have you installed the package? Here is the [link]( library.wolfram.com/infocenter/MathSource/6747) . Download the zip file and install it, then retry the Needs command. $\endgroup$ Commented Dec 4, 2012 at 9:40
  • 1
    $\begingroup$ This solution may no longer work correctly in version 8 and above, as suggested in this question $\endgroup$ Commented Aug 16, 2013 at 17:36
30
$\begingroup$

Without using the "ErrorBarPlots`" Package 

dataX = Sort@RandomReal[1, 10]; dataY = RandomReal[{0.5, 1}, 10]; error = RandomReal[0.5, 10]; errorH = dataY + error; errorL = dataY - error; f[y_] := Transpose[{dataX, y}]; ListLogPlot[{f[errorH], f[errorL], f[dataY]}, Filling -> {1 -> {2}}, Joined -> {False, False, True}]

enter image description here

Edit

Following @rcollyer's suggestion

dataX = Sort@RandomReal[1, 10]; dataY = RandomReal[{0.5, 1}, 10]; error = RandomReal[0.5, 10]; f[y_] := Transpose[{dataX, y}]; PlusMinus[a_, b_] := {a + b, a - b, a}; plusMinList = Thread[PlusMinus[dataY, error]]; ePlot[plotFun_, dataX_, plusMinList_] := plotFun[{ f[plusMinList[[All, 1]]], f[plusMinList[[All, 2]]], f[plusMinList[[All, 3]]]}, Filling -> {1 -> {2}}, Joined -> {False, False, True}] ePlot[ListLogPlot, dataX, plusMinList]
Improve this answer
$\endgroup$
9
  • 1
    $\begingroup$ @rcollyer Thanks! Filling is widely supported by almost all Plotting primitives. I use it always to draw error bars. $\endgroup$ Commented Apr 4, 2012 at 14:59
  • $\begingroup$ This could easily be transformed into a function that accepts the form {_, PlusMinus[_,_} and plots it on the plotting function of your choice: ListPlot, ListLogPlot, etc. $\endgroup$ Commented Apr 4, 2012 at 15:05
  • $\begingroup$ @rcollyer Done :) $\endgroup$ Commented Apr 4, 2012 at 15:57
  • $\begingroup$ I'd put PlusMinus inside of a Block to prevent corrupting Global` , and accept d:{{_, PlusMinus[_,_]}..}. $\endgroup$ Commented Apr 4, 2012 at 16:37
  • 4
    $\begingroup$ Nice! If more traditional error bars are desirable, options can be added: ListLogPlot[..., PlotMarkers -> {"-", "-", "\[FilledCircle]"}] $\endgroup$ Commented Apr 4, 2012 at 17:34
23
$\begingroup$

A one-liner solution (see a bit below lengthy explanation)

This is a bit hacky solution, yet its simplicity prompted me to post it. Load package and make up a data set:

Needs["ErrorBarPlots`"] data = Sort@RandomReal[1, {10, 2}]; error = RandomReal[0.2, 10]; errorplot = ErrorListPlot[Partition[Riffle[data, ErrorBar /@ error], 2], Joined -> True, PlotRange -> All, Frame -> True, Axes -> False]

enter image description here

IMPORTANT: nothing goes below x-axis - not the data, not the error bars. Otherwise your log-scale will break - you cannot take log of negative numbers.

Now lets take a look at the "guts" of the produced graphics:

errorplot // InputForm

enter image description here

Line graphics primitive (sometimes with Offset) applied to sets of points given by coordinates like {x, y}. You just need to replace all these pairs by {x, Log@y}. Careful with Offset - its 1st argument needs to be left a lone. Luckily for us it has an integer 0 so it is easy to avoid applying a pattern that distinguishes it from real numbers we need to deal with.

So here is your one-liner solution:

lerrorplot = errorplot /. {x_Real, y_Real} -> {x, Log@y}

enter image description here

Notice undesirable non-standard ticks on vertical axes (corresponding to log values). To check that it is indeed correct - compare versus ListLogPlot:

check = ListLogPlot[data, Joined -> True, Frame -> True, Axes -> False, PlotStyle -> {Thickness[.03], Orange, Opacity[.3]}]; Show[check, lerrorplot, PlotRange -> All]

enter image description here

A perfect match. Notice the ticks on vertical axes now are in traditional log-scale type (corresponding to original un-scaled data). Of course, your error bars got log-scaled too. Warning: be careful with these ReplaceAll type of solutions - you may be up to a surprise to what exactly is getting replaced. So always analyse your code to avoid unpleasant urprises.

Improve this answer
$\endgroup$
4
  • $\begingroup$ +1, for a straightforward solution. Looking at the code for ErrorListPlot, it uses ReplaceAll to effect its changes. Although it is a little more thorough and discriminating in it's approach. $\endgroup$ Commented Apr 4, 2012 at 13:31
  • $\begingroup$ Nice answer. BTW I liked the ripped-out look of your InputForm picture; Mathematica? It's ideal for pictures that have to convey the message "There's more of this, but that's not important". $\endgroup$ Commented Apr 4, 2012 at 13:40
  • $\begingroup$ @SjoerdC.deVries I use the software is called Snagit. It'd be cool to implement it in Mathematica. $\endgroup$ Commented Apr 4, 2012 at 16:30
  • $\begingroup$ Thanks very much, I ended up using the ErrorBarLogPlot package linked by @Markus Roellig since in the end I need a log-log plot. I tried lerrorplot = errorplot /. {x_Real, y_Real} -> {Log@x, Log@y} but I just got a green box. $\endgroup$ Commented Apr 4, 2012 at 19:25
5
$\begingroup$

According to solution of Dr. Belisarius I wrote this more convenient code:

(* default options needed for error plot *) Options[errListPlot] = { Filling -> {1 -> {2}}, Joined -> {False, False, True}, PlotStyle -> {Black, Black, Directive[Opacity[0.6], Blue]}, FillingStyle -> Black, PlotMarkers -> {Graphics@Line[.04 {{-1, 0}, {1, 0}}], Graphics@Line[.04 {{-1, 0}, {1, 0}}], ""} }; (* plotFun - any ListPlot familly function; data =List ( x, y, error ); opts - usual ListPlot options; *) errListPlot[plotFun_, data_, opts : OptionsPattern[]] := Block[{}, plotFun[{{#[[1]], #[[2]] - #[[3]]} & /@ data, {#[[1]], #[[2]] + #[[3]]} & /@ data, data[[;; , {1, 2}]]}, opts, Sequence @@ Options[errListPlot]] ] data = Table[{i, RandomReal[10], RandomReal[{0.1, 1}]}, {i, 1, 20}]; errListPlot[ListLogPlot, data, PlotRange -> All, Frame -> True, FrameLabel -> {"x label", "y label"}, ImageSize -> 800, BaseStyle -> {18, FontFamily -> "Arial"}]

Resulting plot with error bars First I set necessary options for the plot with Options[errListPlot]. Then the plot function is defined with option pattern. Supplied options will be given to targeted List-XXX-Plot function and applied to the graphics.

Be careful, supplied option will overwrite default options from Options[errListPlot]. This can be useful if you do it right or catastrophic.

Improve this answer
$\endgroup$
3
  • 1
    $\begingroup$ The question requested that the y-axis be logarithmic, not the x-axis. $\endgroup$ Commented Jul 22, 2016 at 17:06
  • 1
    $\begingroup$ This solution works for any combination of log, loglog, loglinear, linearlog plots. Example ListLogPlot: errListPlot[ListLogPlot, data]. $\endgroup$ Commented Jul 25, 2016 at 15:23
  • 1
    $\begingroup$ In that case, you may wish to edit your answer to include a figure that responds directly to the question. Doing so would make your answer more useful to others. Best wishes. $\endgroup$ Commented Jul 25, 2016 at 15:35
5
$\begingroup$

In Mathematica 12, the ErrorBarPlots package was replaced by the built-in Around function and related methods.

Now it's possible to display errorbars on a logarithmic plot using only built-in core functions and the ListLogPlot function:

data = Sort@RandomReal[{2, 5}, {10, 2}]; error = RandomReal[0.5, 10]; toPlot = MapThread[({#1[[1]], Around[#1[[2]], #2]}) &, {data, error}]; ListLogPlot[toPlot, Joined -> True, Frame -> True]

Improve this answer
$\endgroup$
2
  • $\begingroup$ Unfortunately, this will always plot the absolute uncertainties. In Log-scale it is common to plot the relative error to avoid funny artifacts. ErrorBarLogPlots automatically took care of this. Does anybody found a similar functionality in V12? $\endgroup$ Commented Apr 29, 2019 at 14:56
  • 1
    $\begingroup$ @MarkusRoellig By relative uncertainty you mean ±5% for example? If so, you can use Around[x, Scaled[0.05]]. $\endgroup$ Commented Apr 30, 2019 at 17:23

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.