5
$\begingroup$

Does anybody know why the axis label is shifted in this plot? Probably because of the different lengths of the labels of the ticks? How can I have the axis label in the middle of the axis?

The code that generates the plot is

Plot3D[master, {l2, 0, 15}, {l3, 0, 15}, PlotRange -> {0, 0.02}, AxesLabel -> {Style[Subscript[\[Lambda], 2], "Text", Background -> White], Style[Subscript[\[Lambda], 3], "Text", Background -> White], Rotate[Text[Style["I(0,1,1,1)\n", 14]], \[Pi]/2]}, Ticks -> {Automatic, Automatic, {0, 0.01, 0.02}}]

The answer given below works for the mentioned plot. However, another problem occurs in another plot when plotting the range PlotRange -> {-11000000, 11000000} and where the labels on the axes ticks should be $−1⋅10^7$ and $1⋅10^7$ such as Ticks -> {Automatic, Automatic, {{-10000000, "-1*\!\(\*SuperscriptBox[\(10\), \(7\)]\)"}, 0, {10000000, "1*\!\(\*SuperscriptBox[\(10\), \(7\)]\)"}}}]. This does not work with the stated answer below.

Moreover, my label on the vertical axis includes subscripts, which is also not compatible with the suggestions in the answer: Text[ Style["B(\[Gamma])\!\(\*SubscriptBox[\(\[Lambda]\), \ \(2\)]\)\!\(\*SubscriptBox[\(\[Lambda]\), \(3\)]\)", 14]]}

enter image description here

Improve this question
$\endgroup$
6
  • 7
    $\begingroup$ Please include the code that generates the plot. It's notoriously difficult to debug code via telepathy. $\endgroup$ Commented May 3, 2015 at 18:07
  • $\begingroup$ I'm sorry that I forgot to include the code. I just edited my question. $\endgroup$ Commented May 3, 2015 at 19:52
  • $\begingroup$ What do you mean by askew? Which axis label is askew? $\endgroup$ Commented May 3, 2015 at 21:29
  • $\begingroup$ I only see labels aligned to the horizontal or vertical axis. Nothing askew there. $\endgroup$ Commented May 3, 2015 at 21:42
  • $\begingroup$ Please note that by default, labels are displayed horizontally. Rotating it by Pi/2 makes it vertical. Thus the comments about seeing nothing askew. I suspect you would like the label to be parallel to the axis, but admittedly that is a guess. $\endgroup$ Commented May 3, 2015 at 23:21

1 Answer 1

Reset to default
10
$\begingroup$

I assume you are referring to the z-axis label, which is badly behaved (it tends to jump to the top or bottom of the axis on my example plot), especially at certain viewpoints:

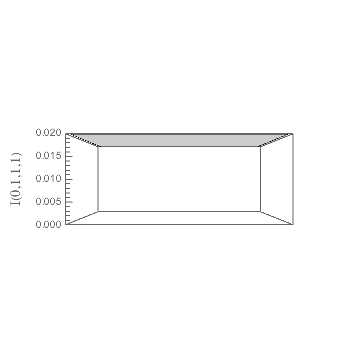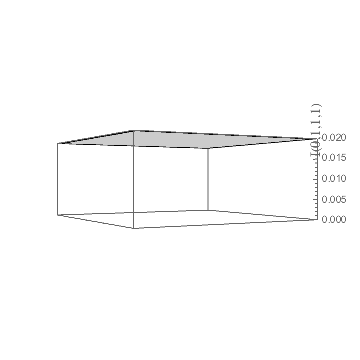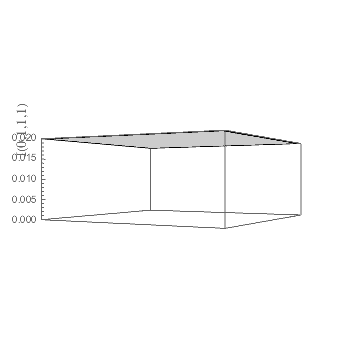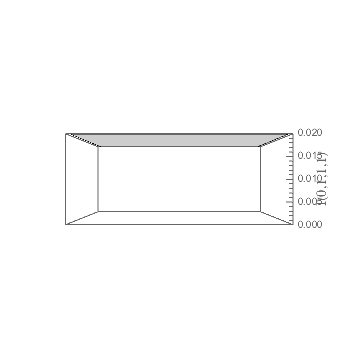
label1

Although, by the nature of perspective in 3D plots, the axes labels will not always appear to be in the middle the the axis, here the position does seem to move out from the midpoint. My first guess was that this had to do with the interaction of the viewpoint and the Rotate applied to the label, but that doesn't seem to be the case, as an unrotated label does the same thing, so my current thought is that Mathematica's built-in label-placement function is struggling to find a clear view with the long numbers needed for the ticks.

Existing Answers

Positioning the label of the z-axis on 3D plots is a topic that has beed addressed here previously in several ways. As long as all you want is a good image of the plot to export, you could just specify the position of the label manually as a new graphic (as in this question) or via Inset with Epilog (here) or with Framed (here). However, these solutions are "static" and do not play well if you want to view your plot interactively by rotating and zooming, etc. This question shows several methods of dealing with axes labels overlapping crowded axes, but I think that the placement of the label in this instance should be addressed.

Workaround using Ticks

There is a "dynamic" work-around, but it is a bit dirty. Essentially, we can abuse Ticks to manually place a new axis label as a tick mark at the axis midpoint. Going through Ticks has the advantage that the label moves with the axis as it is repositioned when the plot is interacted with. We can define a new function for the ticks on the z-axis that includes a label (thanks to this question for the IntegerChop function):

zTicksLabel[ticks__, label_, style_: Null] := Module[ {IntegerChop, nform, nlength, zmin, zmax, t, longest}, IntegerChop = With[{r = Round[#]}, r + Chop[# - r]] &; nform[n_] := Which[ n == 0, n, 10^-5 <= Abs[n] <= 10^5, n, IntegerQ[Log10[Abs[n]]], ScientificForm[N@n, NumberFormat -> (Row[{If[n < 0, "-"], 10^#3}] &)], Divisible[n, 10^Floor@Log10@Abs[n]], ScientificForm[N@n, NumberPoint -> ""], True, ScientificForm[n] ]; nlength = First[ImageSize /. Options[Rasterize@Invisible@nform@#]] &; If[Length@{ticks} == 1, t = IntegerChop@ticks; {zmin, zmax} = {Min@t, Max@t}, {zmin, zmax} = First@{ticks}; t = IntegerChop[N@FindDivisions[{zmin, zmax}, Last@{ticks}]] ]; longest = First@MaximalBy[t, nlength]; Join[ {#, nform@#} & /@ t, {{ Mean[{zmax, zmin}], Row[ {Invisible@nform@longest, If[style === Null, l, Style[l, style]] /. {l -> Rotate[Row[{Invisible["M"], label, Invisible["M"]}], Pi/2]}, Invisible@nform@longest}, Invisible["M"] ] }} ] ];

In response to the comments, I have made this function more sophisticated. The argument ticks, takes either:

  1. an explicit list of tick positions like {tick1, tick2, ...}, in which case only those ticks will be drawn;
  2. or the sequence {zmin, zmax}, n, in which case the function draws about n z-axis ticks between zmin and zmax according to the function FindDivisions (rather than the mysterious Mathematica default).

The argument label takes an expression (which can be anything that can be rotated and given a Style, but in most cases should be a string) and places it somewhat outside a tick in the middle. However, because the label is made with Ticks, it inherits the TickStyle options if they are specified, rather than LabelStyle, so I have left room for style options to be specified explicitly with the style argument. Also, this just rotates the label into a vertical position, rather than aligning it to the z-axis, as has been noted in the comments.

Apply it as so:

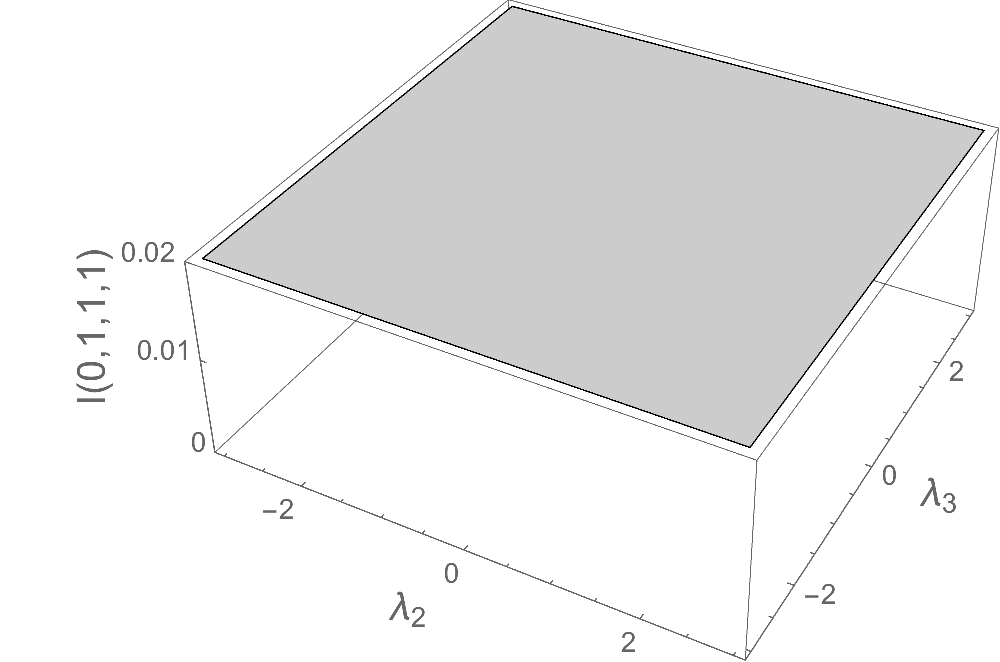
Plot3D[master, {l2, 0, 15}, {l3, 0, 15}, AxesLabel -> {Subscript[\[Lambda], 2], Subscript[\[Lambda], 3], Null}, LabelStyle -> Blue, TicksStyle -> Red, PlotRange -> {0, 0.02}, Ticks -> {Automatic, Automatic, zTicksLabel[{#1, #2}, 3, "I(0,1,1,1)", Orange] &} ]

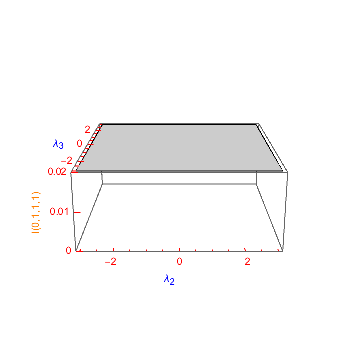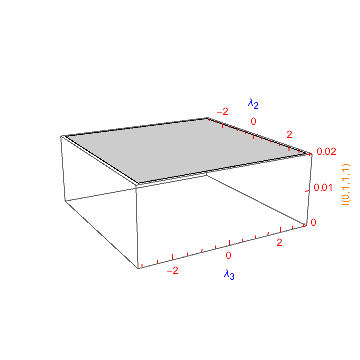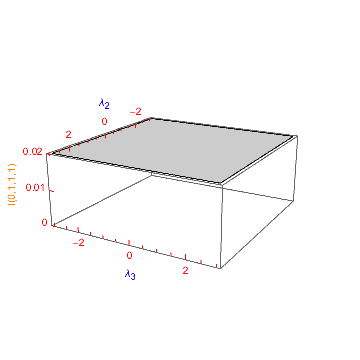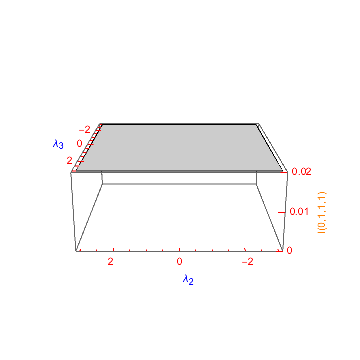
label3

As a further example, to make all axes labels a larger size, we just pass FontSize -> 14 to LabelStyle and the style argument of zTicksLabel (keeping TicksStyle at size 10):

Plot3D[master, {l2, 0, 15}, {l3, 0, 15}, AxesLabel -> {Subscript[\[Lambda], 2], Subscript[\[Lambda], 3], Null}, LabelStyle -> 14, TicksStyle -> 10, PlotRange -> {0, 0.02}, Ticks -> {Automatic, Automatic, zTicksLabel[{#1, #2}, 3, "I(0,1,1,1)", 14] &} ]

label2

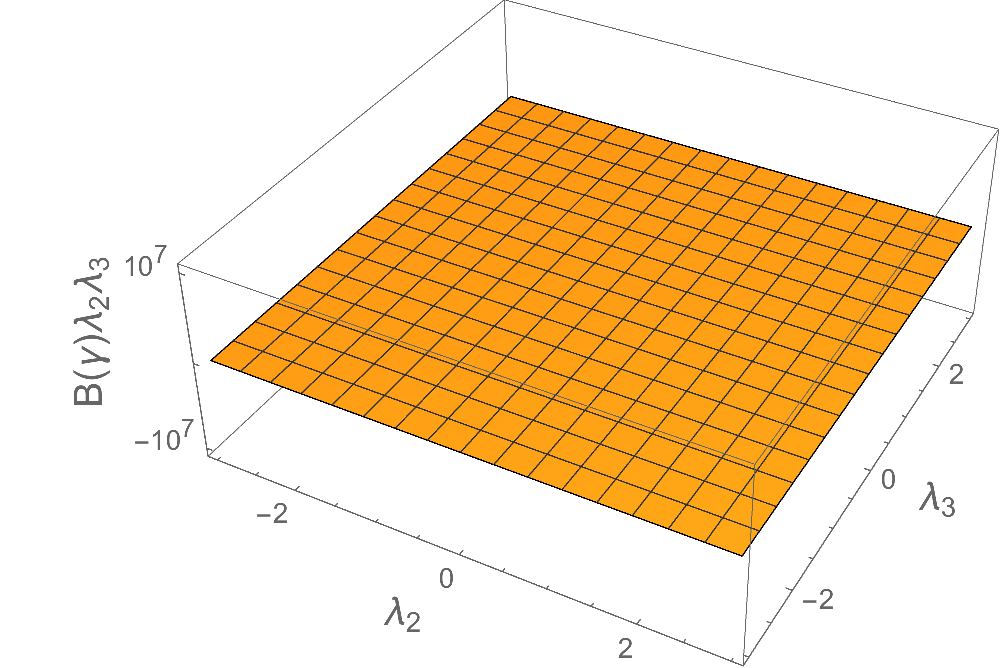
And lastly, if you only want two z-axis ticks at particular locations, do something like 

Plot3D[master, {l2, 0, 15}, {l3, 0, 15}, AxesLabel -> {Subscript[\[Lambda], 2], Subscript[\[Lambda], 3], Null}, LabelStyle -> 14, TicksStyle -> 10, PlotRange -> {-1.1*^7, 1.1*^7}, Ticks -> { Automatic, Automatic, zTicksLabel[{-10^7, 10^7}, "B(\[Gamma])\!\(\*SubscriptBox[\(\[Lambda]\), \(2\)]\)\!(\*SubscriptBox[\(\[Lambda]\), \(3\)]\)", 14] & } ]

label4

Improve this answer
$\endgroup$
8
  • $\begingroup$ Thanks a lot for your answer. It nearly solves my problem. One question remains: How can I make the labels larger? I normally do that with Text[Style["Re[I(0,1,1,1)]\n", 14]]. $\endgroup$ Commented May 4, 2015 at 14:48
  • 1
    $\begingroup$ Pass Directive[FontSize -> 14] as the style argument. I'll edit the post to show this. $\endgroup$ Commented May 4, 2015 at 15:09
  • $\begingroup$ Thank you very much, that solves my problem. $\endgroup$ Commented May 4, 2015 at 16:01
  • $\begingroup$ However, I get a problem in another plot. There I would like to have PlotRange -> {-11000000, 11000000} but the labels on the axes ticks should be $-1\cdot 10^7$ and $1\cdot 10^7$ such as Ticks -> {Automatic, Automatic, {{-10000000, "-1*\!\(\*SuperscriptBox[\(10\), \(7\)]\)"}, 0, {10000000, "1*\!\(\*SuperscriptBox[\(10\), \(7\)]\)"}}}]. Moreover, my label on the vertical axis includes subscripts, which is not compatible with your suggestion: Text[ Style["B(\[Gamma])\!\(\*SubscriptBox[\(\[Lambda]\), \ \(2\)]\)\!\(\*SubscriptBox[\(\[Lambda]\), \(3\)]\)\n", 14]]} $\endgroup$ Commented May 4, 2015 at 21:52
  • $\begingroup$ @LCF, I've updated the zTicksLabel function above to handle a bit more, so it should be able to take care of this now. $\endgroup$ Commented May 5, 2015 at 14:11

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.