For the B-spline curve:
$$ \overset{\rightharpoonup }{C}(u)=\sum _{i=0}^n N_{i,p}(u) \overset{\rightharpoonup }{P}_i \text{ }\qquad (a\leq u\leq b) $$
where, $P_i$ is the control point, the $N_ {i, p} (u)$ are the $p$th - degree B-spline basis functions defined on the non-periodic (and non-uniform) knot vector:
$\{\underbrace {a,\cdots ,a}_{p+1},u_{p+1},\cdots u_{m-p-1},\underbrace {b,\cdots,b}_{p+1}\}$
Here, $m=n+p+1$ and the domain of curve is $[u_p,u_{n+p}]$
For your example
knots = {0,1,2,3,4,5,6,7,8}; points = {{0,0},{1/2,1},{1,1/4},{3/2,1},{2,0}}; weights = {1,1,1,1,1}; degree= 3; f = BSplineFunction[points, SplineDegree -> degree, SplineKnots -> knots, SplineWeights -> weights] So the spline function domain is $[3,5]$, you can verify it via the below code:
GraphicsColumn[ {ParametricPlot[f[u], {u, 3, 5}], Graphics[ {BSplineCurve[points, SplineDegree -> degree, SplineKnots -> knots, SplineWeights -> Automatic]}]}] 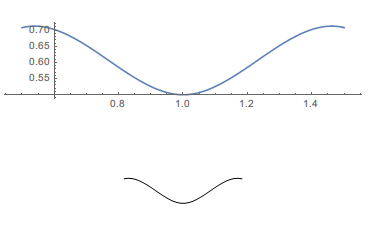
Owing the built-in BSplineFunction[] using the default domain $[0,1]$ to generate the spline icon, so f will lost the spline icon like this:
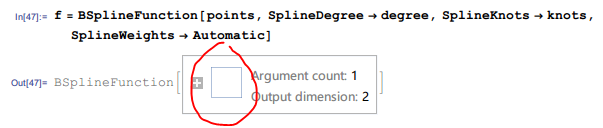
By the normalization of knots,
BSplineFunction[ points, SplineDegree -> degree, SplineKnots -> {-(3/2), -1, -(1/2), 0, 1/2, 1, 3/2, 2, 5/2}, SplineWeights -> Automatic] 
