I don't very content with current method.So a better solution is expected still.I hope the it meet that two conditions.

1. That space is approximately equivalence.
2. We can control how many points to produce.

v11.1 provides a new function SpherePoints. As the Details

SpherePoints[n] gives exactly equally spaced points in certain cases for small n. In other cases, it places points so they are approximately equally spaced.

Can we achieve the same goal i.e. approximately equally spaced points in an arbitrary 2D Region?

The following is my attempt based on Union:

SeedRandom[1] region = ConvexHullMesh[RandomReal[1, {100, 2}]]; UniformPts = Union[RandomPoint[region, 50000], SameTest -> (EuclideanDistance[#1, #2] < .1 &)]; Show[region, Graphics[Point[UniformPts]]]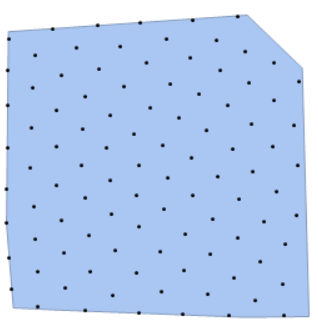 

Nevertheless, this approach has two weakness:

1. It is slow with a large number of pre-generated points i.e. the 2nd argument of RandomPoint, while the space won't be uniform enough if I don't pre-generate enough points, here's an example:

2. The number of resulting points isn't controllable.