Here is one method, now more robust:
pwSplit[_[pairs : {{_, _} ..}]] := Piecewise[{#}, Indeterminate] & /@ pairs
pwSplit[_[pairs : {{_, _} ..}, expr_]] :=
Append[pwSplit@{pairs}, pwSplit@{{{expr, Nor @@ pairs[[All, 2]]}}}]
Testing:
pw = Piecewise[{{x^2, x < 0}, {x, 2 > x > 0}, {Log[x], x > 2}}];
Plot[Evaluate[pwSplit@pw], {x, -2, 4}, PlotStyle -> Thick, Axes -> False]

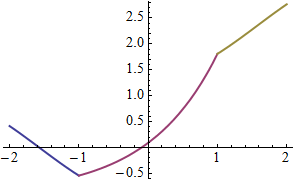
pw = Integrate[Piecewise[{{E^x, x^2 <= 1}}, Sin[x]], x];
Plot[Evaluate[pwSplit @ pw], {x, -2, 2}, PlotStyle -> Thick, PlotRange -> Full]
----------
I like Heike's method so much I have to do my own version of it.
Module[{i = 1},
Plot[pw, {x, -2, 2}, PlotStyle -> Thick]
/. x_Line :> {ColorData[1][i++], x}
]
