Borrowing almost verbatim from a recent response about finding [extrema](https://mathematica.stackexchange.com/questions/5575/5591#5591), here is a method that is useful when your function is differentiable and hence can be "tracked" by `NDSolve`.
f[x_] := BesselJ[1, x]^2 + BesselK[1, x]^2 - Sin[Sin[x]]
In[191]:= zeros =
Reap[soln =
y[x] /. First[
NDSolve[{y'[x] == Evaluate[D[f[x], x]], y[10] == (f[10])},
y[x], {x, 10, 0},
Method -> {"EventLocator", "Event" -> y[x],
"EventAction" :> Sow[{x, y[x]}]}]]][[2, 1]]
During evaluation of In[191]:=
NDSolve::mxst: Maximum number of 10000 steps reached at the point
x == 1.5232626281716416`*^-124. >>
Out[191]= {{9.39114, 8.98587*10^-16}, {6.32397, -3.53884*10^-16},
{3.03297, -8.45169*10^-13}, {0.886605, -4.02456*10^-15}}
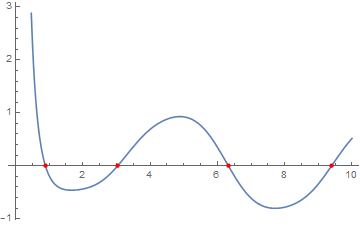
Plot[f[x], {x, 0, 10},
Epilog -> {PointSize[Medium], Red, Point[zeros]}]

If it were a trickier function, one might use `Method -> {"Projection", ...}` to enforce the condition that `y[x]` is really the same as `f[x]`. This method may be useful in situations (if you can find them) where we have one function in one variable, and `Reduce` either cannot handle it or takes a long time to do so.
---
**Addendum by J. M.**
`WhenEvent` is now the documented way to include event detection in `NDSolve`, so using it along with the trick of [specifying an empty list where the function should be](https://reference.wolfram.com/language/tutorial/NDSolveWhenEvents.html#32663), here's how to get a pile of zeroes:
f[x_] := BesselJ[1, x]^2 + BesselK[1, x]^2 - Sin[Sin[x]]
zeros = Reap[NDSolve[{y'[x] == D[f[x], x], WhenEvent[y[x] == 0, Sow[{x, y[x]}]],
y[10] == f[10]}, {}, {x, 10, 0}]][[-1, 1]];
Plot[f[x], {x, 0, 10}, Epilog -> {PointSize[Medium], Red, Point[zeros]}]