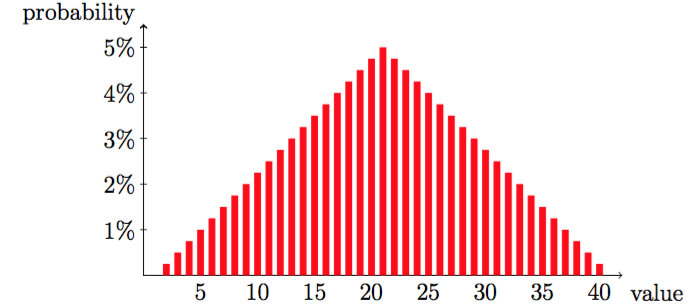
Usually, 20-sided dice are labeled with the numbers 1 to 20. When you roll two of these, their sum is a random number between 2 and 40. The total 21 is most likely to occur, while 2 and 40 are the least. The probabilities vary linearly in between, as shown below.
Is there a different way to label two 20-sided dice with positive integers, so that their sum is still a random number between 2 and 40 with these same probabilities?
Without the positive integer constraint, there would be trivial solutions like [0, ... ,19] and [1, ... ,21], or [0.5, ... ,19.5] and [1.5, ... ,20.5].
This is a variant of a more famous puzzle, which asks the same question for six-sided dice.