Transpilation into custom gate set in qiskit

The Qiskit standard gate list

You can find the full list of Qiskit standard gates in the module qiskit.circuit.library.standard_gates (documentation).

The matrix representation of a standard gate

For each gate, you can see its matrix representation with the to_matrix method. For example:

from qiskit.circuit.library import standard_gates standard_gates.HGate().to_matrix() 

array([[ 0.70710678+0.j, 0.70710678+0.j], [ 0.70710678+0.j, -0.70710678+0.j]]) 

Or, its latex representation:

from qiskit.visualization import array_to_latex array_to_latex(standard_gates.HGate().to_matrix()) 

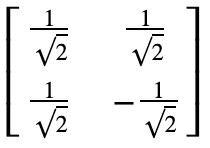
Creating your own custom gate

You can create your own gates from a circuit. For example:

from qiskit import QuantumCircuit custom_circuit = QuantumCircuit(2, name='bell') custom_circuit.h(0) custom_circuit.cx(0, 1) custom_gate = custom_circuit.to_gate() 

You can create a circuit using that custom gate:

circuit = QuantumCircuit(3) circuit.h(0) circuit.append(custom_gate, [0,1]) circuit.cx(1, 2) circuit.draw() 

 ┌───┐┌───────┐ q_0: ┤ H ├┤0 ├───── └───┘│ bell │ q_1: ─────┤1 ├──■── └───────┘┌─┴─┐ q_2: ──────────────┤ X ├ └───┘ 

Telling the transpiler not to decompose your custom gate

Following the previous example, you can transpile that circuit using the custom gate name in the target basis list:

from qiskit.compiler import transpile basis_gates = ['bell', 'u3', 'cx'] qc_trans = transpile(circuit, basis_gates=basis_gates) qc_trans.draw() 

 ┌─────────────┐┌───────┐ q_0: ┤ U3(π/2,0,π) ├┤0 ├───── └─────────────┘│ bell │ q_1: ───────────────┤1 ├──■── └───────┘┌─┴─┐ q_2: ────────────────────────┤ X ├ └───┘ 

Your custom gate as basis target of a circuit that is not using it

You can basis-target your own custom in some cases. That requires to extend the equivalence library. Following your mycx example:

1. Create a circuit definition with your custom gate

mycx = QuantumCircuit(2, name='mycx') mycx.cx(0, 1) mycx_def = QuantumCircuit(2) mycx_def.append(mycx.to_gate(), [0, 1]) 

2. Add an equivalence to the library where a gate (CXGate in this case) is equivalent to that definition.

StandardEquivalenceLibrary.add_equivalence(CXGate(), mycx_def) 

3. Create a circuit that uses the domain gate (CXGate in this case).

from qiskit.compiler import transpile qc = QuantumCircuit(3) qc.h(0) qc.cx(0, 1) qc.cx(1, 2) 

4. Transpile using the parameter translation_method='translator'. This will tell the transpiler to use the equivalence library for basis translation. In the basis_gate parameter you can refer to your custom gate name (mycx in this case):

result = transpile(qc, basis_gates=['mycx', 'u3'], translation_method='translator') result.draw() 

 ┌─────────────┐┌───────┐ q_0: ┤ U3(π/2,0,π) ├┤0 ├───────── └─────────────┘│ mycx │┌───────┐ q_1: ───────────────┤1 ├┤0 ├ └───────┘│ mycx │ q_2: ────────────────────────┤1 ├ └───────┘ 

You can use BQSKit to accomplish this very easily. BQSKit is a powerful and portable quantum compiler/transpiler. You will need to calculate the unitary of your gate and you can just plug that into BQSKit.

You can accomplish this with the following:

from bqskit import compile, MachineModel, Circuit from bqskit.ir.gates import IdentityGate, ConstantUnitaryGate mycx = ConstantUnitaryGate([...]) # Fill in unitary here model = MachineModel(gate_set={mycx, IdentityGate(1)}) output_circuit = compile(circuit, model)