Wolfram Function Repository

Instant-use add-on functions for the Wolfram Language

Function Repository Resource:

 ExtendedLatticeReduce

Source Notebook

Compute a reduced basis for a set of vectors, along with a unimodular matrix that converts from the vectors to the reduced basis

Contributed by: Daniel Lichtblau

ResourceFunction["ExtendedLatticeReduce"][lat]

computes a reduced basis ℬ for the lattice of integer vectors lat, returning the pair {𝒰,ℬ}, where 𝒰 is a unimodular conversion matrix satisfying 𝒰.lat=ℬ.

Details and Options

The input lattice lat must be a matrix of integers and/or rational numbers. Gaussian integers and rationals are also permitted.
The conversion matrix is square and unimodular (it has determinant equal to ±1).
ResourceFunction["ExtendedLatticeReduce"][lat,"ReductionLambda"→λ] will use the value λ for the reduction ratio in the LLL algorithm.
The reduction ratio λ must be in the range 1/4 ≤ λ<1.
The value of the "ReductionLambda" option setting can affect the speed and quality of the reduction. A lower value will typically give a faster computation, but result in a lattice that is further from being fully reduced (it will of course be reduced in the LLL sense appropriate for the parameter setting).

Examples

Basic Examples (5) 

Create an integer lattice comprised of two columns of large integers augmented on the right by an identity matrix:

In[1]:=
SeedRandom[1234]; lat = Join[RandomInteger[{-10^8, 10^8}, {4, 2}], IdentityMatrix[4], 2]
Out[1]=

Reduce the lattice:

In[2]:=
{umat, redlat} = ResourceFunction["ExtendedLatticeReduce"][lat]
Out[2]=

Check the conversion matrix equation:

In[3]:=
umat . lat - redlat
Out[3]=

Check that the conversion matrix is unimodular:

In[4]:=
Det[umat]
Out[4]=

Check that LatticeReduce gives the same reduced lattice (this is not strictly necessary):

In[5]:=
LatticeReduce[lat]
Out[5]=

Scope (2) 

Create a rational lattice:

In[6]:=
SeedRandom[1234]; lat = RandomInteger[{-10^8, 10^8}, {4, 5}]/ RandomInteger[{1, 10^3}, {4, 5}]
Out[6]=

Compute a reduction of the lattice along with the corresponding unimodular conversion matrix::

In[7]:=
{umat, redlat} = ResourceFunction["ExtendedLatticeReduce"][lat]
Out[7]=

Reduce a lattice of Gaussian integers with larger entries in the leftmost two columns:

In[8]:=
SeedRandom[1234]; c1 = 2; c2 = 5; lat = Join[ RandomInteger[{-10^8, 10^8}, {4, c1}] + I*RandomInteger[{-10^8, 10^8}, {4, c1}], RandomInteger[{-10^3, 10^3}, {4, c2}] + I*RandomInteger[{-10^3, 10^3}, {4, c2}], 2]; {umat, redlat} = ResourceFunction["ExtendedLatticeReduce"][lat]
Out[8]=

Check the result:

In[9]:=
{Det[umat], Max[Abs[umat . lat - redlat]]}
Out[9]=

Options (7) 

ReductionLambda (7) 

Create a large matrix with big integers in the first two columns and an identity matrix on the right:

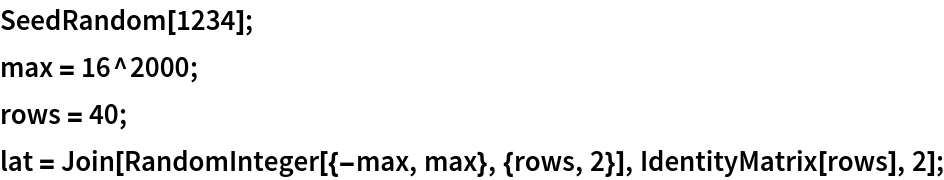
First compute the default reduction:

In[10]:=
Timing[{umat, redlat} = ResourceFunction["ExtendedLatticeReduce"][lat];]
Out[10]=

Check the conversion matrix criteria:

In[11]:=
{Abs[Det[umat]] == 1, Max[Abs[umat . lat - redlat]] == 0}
Out[11]=

Computing a reduction of higher quality typically takes longer:

In[12]:=
Timing[{umat2, redlat2} = ResourceFunction["ExtendedLatticeReduce"][lat, "ReductionLambda" -> 0.999];]
Out[12]=

Using a smaller reduction size ratio setting typically gives a faster computation:

In[13]:=
Timing[{umat3, redlat3} = ResourceFunction["ExtendedLatticeReduce"][lat, "ReductionLambda" -> 1/4];]
Out[13]=

The higher quality reduction manifests by most rows in the “stronger” result having norms smaller than for corresponding rows in the default reduction:

In[14]:=
Map[Norm[N[#]] &, redlat2]/Map[Norm[N[#]] &, redlat]
Out[14]=

The lower quality reduction manifests by most rows in the “weaker” result having norms larger than for corresponding rows in the default reduction:

In[15]:=
Map[Norm[N[#]] &, redlat3]/Map[Norm[N[#]] &, redlat]
Out[15]=

Version History

  • 2.0.0 – 26 May 2021
  • 1.0.0 – 07 October 2019

Source Metadata

Related Resources

Author Notes

A different implementation of this functionality, written by Wilberd van der Kallen, is available at the Wolfram Library Archive link provided.

Version 2 uses a "sometimes asymptotically fast" divide-and-conquer algorithm similar to that used in the half-GCD algorithm for integer GCD computations. This is done whenever the input lattice consists of integers or Gaussian integers and has full row rank. A more rigorous version is informally referred to as L1Plus. The theory behind it is in the links. This implementation qualities as "quick and dirty" and does not come with any guarantee about asymptotic speed other than it promises to try hard and do the best it can.

License Information