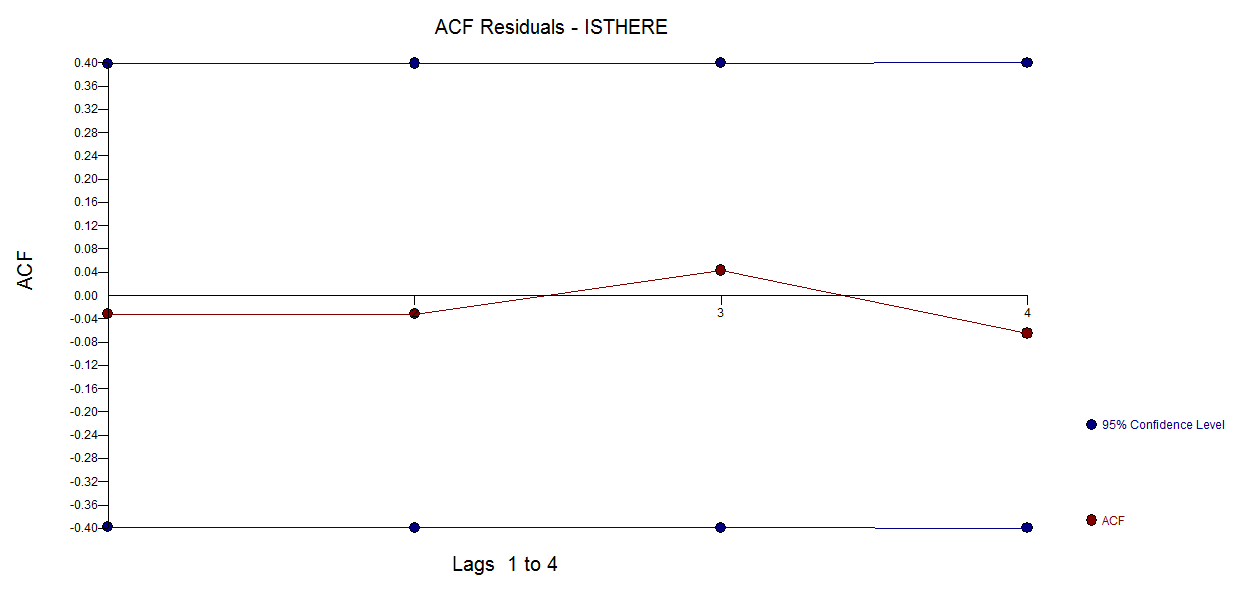
The problem that you have "I am unable to use classic linear regression due to strong temporal (serial) auto-correlation among values." is in reality an opportunity. I took your 27 values and used AUTOBOX a piece of software (which I have helped develop) that can (optionally) automatically determine a possible model. Here is the actual/fit and forecast graph 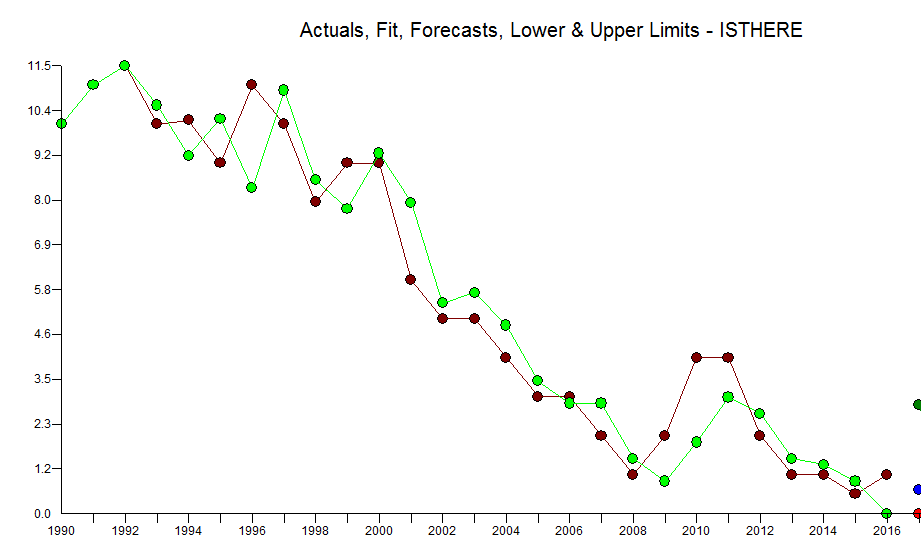 . The ACF of the residuals is here with residual plot here
. The ACF of the residuals is here with residual plot here 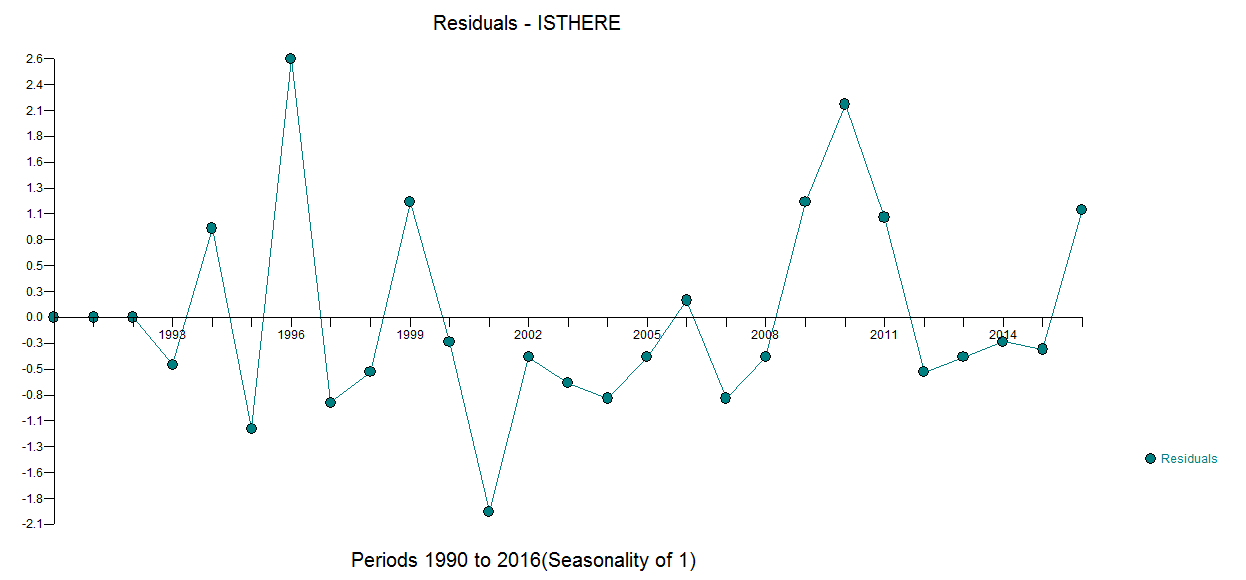 . The model is here
. The model is here 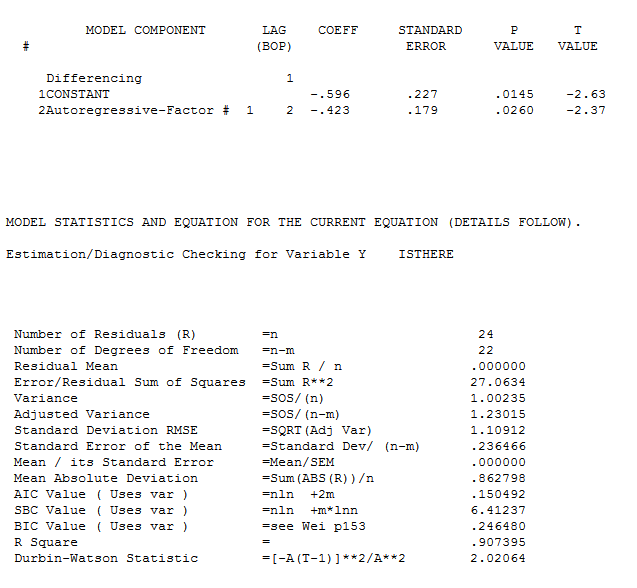 and here
and here 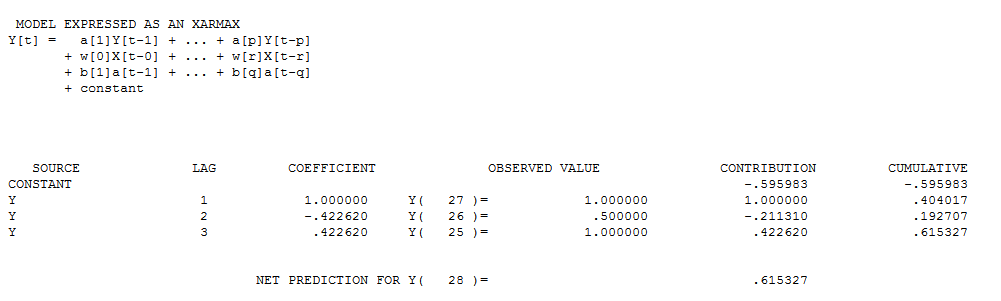 and here
and here 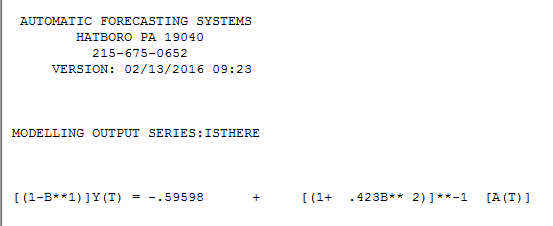 . Two coefficients aptly describe the data with estimated "trend" aka "drift" i.e. period to period differential of -.596. Note that this is one kind of trend where your model used the counting numbers 1,2,...27 as a predictor variable. If your data suggested that kind of trend then the software would have found it to be more applicable. I will try and find an earlier post of mine which fully detailed/contrasted these two kinds of trends. Here Identifying a stochastic trend modelIdentifying a stochastic trend model and Detecting initial trend or outliersDetecting initial trend or outliers
. Two coefficients aptly describe the data with estimated "trend" aka "drift" i.e. period to period differential of -.596. Note that this is one kind of trend where your model used the counting numbers 1,2,...27 as a predictor variable. If your data suggested that kind of trend then the software would have found it to be more applicable. I will try and find an earlier post of mine which fully detailed/contrasted these two kinds of trends. Here Identifying a stochastic trend modelIdentifying a stochastic trend model and Detecting initial trend or outliersDetecting initial trend or outliers
The problem that you have "I am unable to use classic linear regression due to strong temporal (serial) auto-correlation among values." is in reality an opportunity. I took your 27 values and used AUTOBOX a piece of software (which I have helped develop) that can (optionally) automatically determine a possible model. Here is the actual/fit and forecast graph  . The ACF of the residuals is here with residual plot here
. The ACF of the residuals is here with residual plot here  . The model is here
. The model is here  and here
and here  and here
and here  . Two coefficients aptly describe the data with estimated "trend" aka "drift" i.e. period to period differential of -.596. Note that this is one kind of trend where your model used the counting numbers 1,2,...27 as a predictor variable. If your data suggested that kind of trend then the software would have found it to be more applicable. I will try and find an earlier post of mine which fully detailed/contrasted these two kinds of trends. Here Identifying a stochastic trend model and Detecting initial trend or outliers
. Two coefficients aptly describe the data with estimated "trend" aka "drift" i.e. period to period differential of -.596. Note that this is one kind of trend where your model used the counting numbers 1,2,...27 as a predictor variable. If your data suggested that kind of trend then the software would have found it to be more applicable. I will try and find an earlier post of mine which fully detailed/contrasted these two kinds of trends. Here Identifying a stochastic trend model and Detecting initial trend or outliers
The problem that you have "I am unable to use classic linear regression due to strong temporal (serial) auto-correlation among values." is in reality an opportunity. I took your 27 values and used AUTOBOX a piece of software (which I have helped develop) that can (optionally) automatically determine a possible model. Here is the actual/fit and forecast graph  . The ACF of the residuals is here with residual plot here
. The ACF of the residuals is here with residual plot here  . The model is here
. The model is here  and here
and here  and here
and here  . Two coefficients aptly describe the data with estimated "trend" aka "drift" i.e. period to period differential of -.596. Note that this is one kind of trend where your model used the counting numbers 1,2,...27 as a predictor variable. If your data suggested that kind of trend then the software would have found it to be more applicable. I will try and find an earlier post of mine which fully detailed/contrasted these two kinds of trends. Here Identifying a stochastic trend model and Detecting initial trend or outliers
. Two coefficients aptly describe the data with estimated "trend" aka "drift" i.e. period to period differential of -.596. Note that this is one kind of trend where your model used the counting numbers 1,2,...27 as a predictor variable. If your data suggested that kind of trend then the software would have found it to be more applicable. I will try and find an earlier post of mine which fully detailed/contrasted these two kinds of trends. Here Identifying a stochastic trend model and Detecting initial trend or outliers
The problem that you have "I am unable to use classic linear regression due to strong temporal (serial) auto-correlation among values." is in reality an opportunity. I took your 27 values and used AUTOBOX a piece of software (which I have helped develop) that can (optionally) automatically determine a possible model. Here is the actual/fit and forecast graph  . The ACF of the residuals is here with residual plot here
. The ACF of the residuals is here with residual plot here  . The model is here
. The model is here  and here
and here  and here
and here  . Two coefficients aptly describe the data with estimated "trend" aka "drift" i.e. period to period differential of -.596. Note that this is one kind of trend where your model used the counting numbers 1,2,...27 as a predictor variable. If your data suggested that kind of trend then the software would have found it to be more applicable. I will try and find an earlier post of mine which fully detailed/contrasted these two kinds of trends. Here Identifying a stochastic trend model and Detecting initial trend or outliers
. Two coefficients aptly describe the data with estimated "trend" aka "drift" i.e. period to period differential of -.596. Note that this is one kind of trend where your model used the counting numbers 1,2,...27 as a predictor variable. If your data suggested that kind of trend then the software would have found it to be more applicable. I will try and find an earlier post of mine which fully detailed/contrasted these two kinds of trends. Here Identifying a stochastic trend model and Detecting initial trend or outliers
The problem that you have "I am unable to use classic linear regression due to strong temporal (serial) auto-correlation among values." is in reality an opportunity. I took your 27 values and used AUTOBOX a piece of software (which I have helped develop) that can (optionally) automatically determine a possible model. Here is the actual/fit and forecast graph  . The ACF of the residuals is here with residual plot here
. The ACF of the residuals is here with residual plot here  . The model is here
. The model is here  and here
and here  and here
and here  . Two coefficients aptly describe the data with estimated "trend" i.e. period to period differential of -.596. Note that this is one kind of trend where your model used the counting numbers 1,2,...27 as a predictor variable. If your data suggested that kind of trend then the software would have found it to be more applicable. I will try and find an earlier post of mine which fully detailed/contrasted these two kinds of trends. Here Identifying a stochastic trend model and Detecting initial trend or outliers
. Two coefficients aptly describe the data with estimated "trend" i.e. period to period differential of -.596. Note that this is one kind of trend where your model used the counting numbers 1,2,...27 as a predictor variable. If your data suggested that kind of trend then the software would have found it to be more applicable. I will try and find an earlier post of mine which fully detailed/contrasted these two kinds of trends. Here Identifying a stochastic trend model and Detecting initial trend or outliers
The problem that you have "I am unable to use classic linear regression due to strong temporal (serial) auto-correlation among values." is in reality an opportunity. I took your 27 values and used AUTOBOX a piece of software (which I have helped develop) that can (optionally) automatically determine a possible model. Here is the actual/fit and forecast graph  . The ACF of the residuals is here with residual plot here
. The ACF of the residuals is here with residual plot here  . The model is here
. The model is here  and here
and here  and here
and here  . Two coefficients aptly describe the data with estimated "trend" aka "drift" i.e. period to period differential of -.596. Note that this is one kind of trend where your model used the counting numbers 1,2,...27 as a predictor variable. If your data suggested that kind of trend then the software would have found it to be more applicable. I will try and find an earlier post of mine which fully detailed/contrasted these two kinds of trends. Here Identifying a stochastic trend model and Detecting initial trend or outliers
. Two coefficients aptly describe the data with estimated "trend" aka "drift" i.e. period to period differential of -.596. Note that this is one kind of trend where your model used the counting numbers 1,2,...27 as a predictor variable. If your data suggested that kind of trend then the software would have found it to be more applicable. I will try and find an earlier post of mine which fully detailed/contrasted these two kinds of trends. Here Identifying a stochastic trend model and Detecting initial trend or outliers
The problem that you have "I am unable to use classic linear regression due to strong temporal (serial) auto-correlation among values." is in reality an opportunity. I took your 27 values and used AUTOBOX a piece of software (which I have helped develop) that can (optionally) automatically determine a possible model. Here is the actual/fit and forecast graph  . The ACF of the residuals is here with residual plot here
. The ACF of the residuals is here with residual plot here  . The model is here
. The model is here  and here
and here  and here
and here  . Two coefficients aptly describe the data with estimated "trend" i.e. period to period differential of -.596. Note that this is one kind of trend where your model used the counting numbers 1,2,...27 as a predictor variable. If your data suggested that kind of trend then the software would have found it to be more applicable. I will try and find an earlier post of mine which fully detailed/contrasted these two kinds of trends. Here Identifying a stochastic trend model and Detecting initial trend or outliers
. Two coefficients aptly describe the data with estimated "trend" i.e. period to period differential of -.596. Note that this is one kind of trend where your model used the counting numbers 1,2,...27 as a predictor variable. If your data suggested that kind of trend then the software would have found it to be more applicable. I will try and find an earlier post of mine which fully detailed/contrasted these two kinds of trends. Here Identifying a stochastic trend model and Detecting initial trend or outliers
The problem that you have "I am unable to use classic linear regression due to strong temporal (serial) auto-correlation among values." is in reality an opportunity. I took your 27 values and used AUTOBOX a piece of software (which I have helped develop) that can (optionally) automatically determine a possible model. Here is the actual/fit and forecast graph  . The ACF of the residuals is here with residual plot here
. The ACF of the residuals is here with residual plot here  . The model is here
. The model is here  and here
and here  and here
and here  . Two coefficients aptly describe the data with estimated "trend" i.e. period to period differential of -.596. Note that this is one kind of trend where your model used the counting numbers 1,2,...27 as a predictor variable. If your data suggested that kind of trend then the software would have found it to be more applicable. I will try and find an earlier post of mine which fully detailed/contrasted these two kinds of trends. Here Identifying a stochastic trend model and
. Two coefficients aptly describe the data with estimated "trend" i.e. period to period differential of -.596. Note that this is one kind of trend where your model used the counting numbers 1,2,...27 as a predictor variable. If your data suggested that kind of trend then the software would have found it to be more applicable. I will try and find an earlier post of mine which fully detailed/contrasted these two kinds of trends. Here Identifying a stochastic trend model and
The problem that you have "I am unable to use classic linear regression due to strong temporal (serial) auto-correlation among values." is in reality an opportunity. I took your 27 values and used AUTOBOX a piece of software (which I have helped develop) that can (optionally) automatically determine a possible model. Here is the actual/fit and forecast graph  . The ACF of the residuals is here with residual plot here
. The ACF of the residuals is here with residual plot here  . The model is here
. The model is here  and here
and here  and here
and here  . Two coefficients aptly describe the data with estimated "trend" i.e. period to period differential of -.596. Note that this is one kind of trend where your model used the counting numbers 1,2,...27 as a predictor variable. If your data suggested that kind of trend then the software would have found it to be more applicable. I will try and find an earlier post of mine which fully detailed/contrasted these two kinds of trends. Here Identifying a stochastic trend model and Detecting initial trend or outliers
. Two coefficients aptly describe the data with estimated "trend" i.e. period to period differential of -.596. Note that this is one kind of trend where your model used the counting numbers 1,2,...27 as a predictor variable. If your data suggested that kind of trend then the software would have found it to be more applicable. I will try and find an earlier post of mine which fully detailed/contrasted these two kinds of trends. Here Identifying a stochastic trend model and Detecting initial trend or outliers