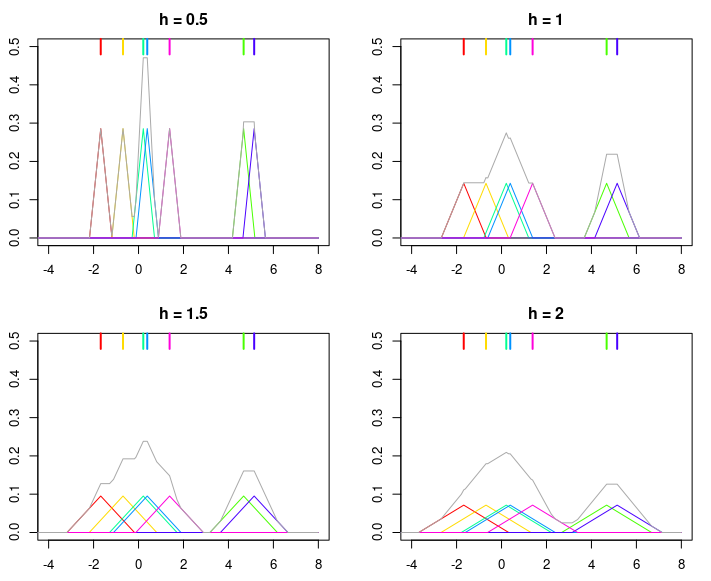
set.seed(123) n <- 7 x <- rnorm(n, sd = 3) K <- function(x) ifelse(x >= -1 & x <= 1, 1 - abs(x), 0) kde <- function(x, data, h, K) { n <- length(data) out <- outer(x, data, function(xi,yi) K((xi-yi)/h)) rowSums(out)/(n*h) } xx = seq(-8, 8, by = 0.001) for (h in c(0.5, 1, 1.5, 2)) { plot(NA, xlim = c(-4, 8), ylim = c(0, 0.5), xlab = "", ylab = "", main = paste0("h = ", h)) for (i in 1:n) { lines(xx, K((xx-x[i])/h)/n(n*h), type = "l", col = rainbow(n)[i]) rug(x[i], lwd = 2, col = rainbow(n)[i], side = 3, ticksize = 0.075) } lines(xx, kde(xx, x, h, K), col = "darkgray") }