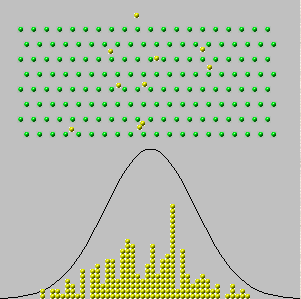
The nicest animation I know: http://www.ms.uky.edu/~mai/java/stat/GaltonMachine.html
The simplest words I have read: http://elonen.iki.fi/articles/centrallimit/index.en.html
If you sum the results of these ten throws, what you get is likely to be closer to 30-40 than the maximum, 60 (all sixes) or on the other hand, the minumum, 10 (all ones).
The reason for this is that you can get the middle values in many more different ways than the extremes. Example: when throwing two dice: 1+6 = 2+5 = 3+4 = 7, but only 1+1 = 2 and only 6+6 = 12.
That is: even though you get any of the six numbers equally likely when throwing one die, the extremes are less probable than middle values in sums of several dice.