Summary: It is often said that Beta distribution is a distribution on distributions! But what is means?
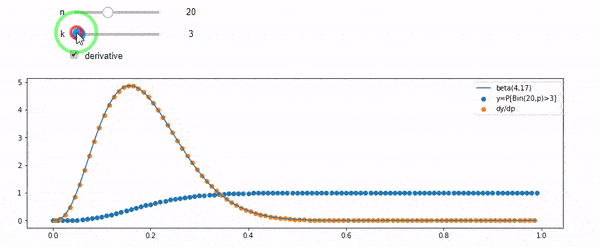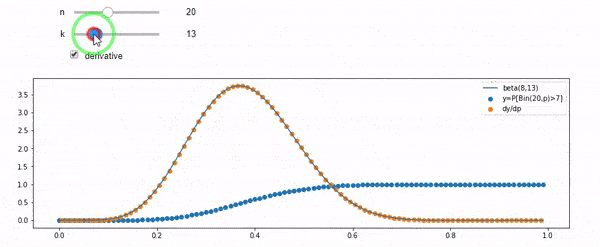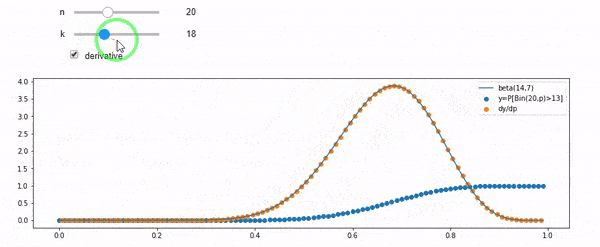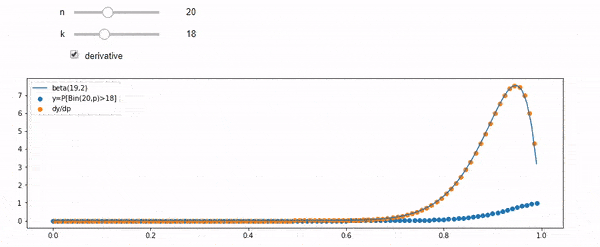
It essentially means that you may fix $n,k$ and think of $\mathbb P[Bin(n,p)\geqslant k]$ as a function of $p$. What thisthe calculation essentiallybelow says is that the value of $\mathbb P[Bin(n,p)\geqslant k]$ increases from $0$ to $1$ when you tune $p$ from $0$ to $1$. The increasing rate at each $p$ is exactly $\beta(k,n-k+1)$ at that $p$.
Let $Bin(n,p)$ denote a Binomial random variable with $n$ samples and the probability of success $p$. Using basic algebra we have
$$\frac d{dp}\mathbb P[Bin(n,p)=i]=n\Big(\mathbb P[Bin(n-1,p)=i-1]-\mathbb P[Bin(n-1,p)=i]\Big).$$
It has also some nice combinatorial proof, think of it as an exercise!
So, we have:
$$\frac d{dp}\mathbb P[Bin(n,p)\geqslant k]=\frac d{dp}\sum_{i=k}^{n}\mathbb P[Bin(n,p)=i]=n\Big(\sum_{i=k}^{n}\mathbb P[Bin(n-1,p)=i-1]-\mathbb P[Bin(n-1,p)=i]\Big)$$ which is a telescoping series and can be simplified as
$$\frac d{dp}\mathbb P[Bin(n,p)\geqslant k]=n\mathbb P[Bin(n-1,p)=k-1]=\frac{n!}{(k-1)!(n-k)!}p^{k-1}(1-p)^{n-k}=\beta(k,n-k+1).$$
Remark To see an interactive version of the plot look at this. You may download the notebook or just use the Binder link.