Most of the answers here seem to cover two approaches: Bayesian and the order statistic. I'd like to add a viewpoint from the binomial, which I think the easiest to grasp.
The intuition for a beta distribution comes into play when we look at it from the lens of the binomial distribution.
The difference between the binomial and the beta is that the former models the number of occurrences ($x$), while the latter models the probability ($p$) itself. In other words, the probability is a parameter in binomial; In the Beta, the probability is a random variable.
Interpretation of $\boldsymbol{\alpha}$, $\boldsymbol{\beta}$
You can think of $\alpha-1$ as the number of successes and $\beta-1$ as the number of failures, just like $n$ & $n-x$ terms in binomial. You can choose the $\alpha$ and $\beta$ parameters however you think they are supposed to be. If you think the probability of success is very high, let's say 90%, set 90 for $\alpha$ and 10 for $\beta$. If you think otherwise, 90 for $\beta$ and 10 for $\alpha$.
As $\alpha$ becomes larger (more successful events), the bulk of the probability distribution will shift towards the right, whereas an increase in $\beta$ moves the distribution towards the left (more failures). Also, the distribution will narrow if both $\alpha$ and $\beta$ increase, for we are more certain.
The Intuition behind the shapes
The PDF of Beta distribution can be U-shaped with asymptotic ends, bell-shaped, strictly increasing/decreasing or even straight lines. As you change $\alpha$ or $\beta$, the shape of the distribution changes.
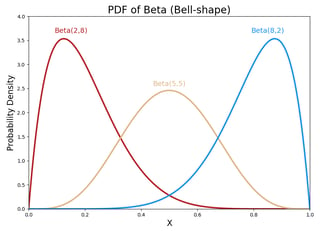
a. Bell-shape
Notice that the graph of PDF with $\alpha = 8$ and $\beta = 2$ is in blue, not in read. The x-axis is the probability of success. The PDF of a beta distribution is approximately normal if $\alpha +\beta$ is large enough and $\alpha$ & $\beta$ are approximately equal.
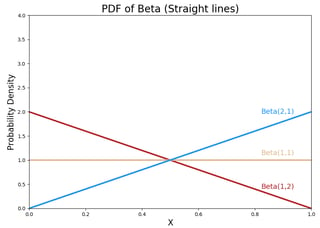
b. Straight Lines
The beta PDF can be a straight line too.
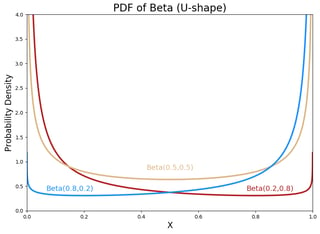
c. U-shape
When $\alpha <1$, $\beta<1$, the PDF of the Beta is U-shaped.
The Intuition behind the shapes
Why would Beta(2,2) be bell-shaped?
If you think of $\alpha-1$ as the number of successes and $\beta-1$ as the number of failures, Beta(2,2) means you got 1 success and 1 failure. So it makes sense that the probability of the success is highest at 0.5.
Also, Beta(1,1) would mean you got zero for the head and zero for the tail. Then, your guess about the probability of success should be the same throughout [0,1]. The horizontal straight line confirms it.
What’s the intuition for Beta(0.5, 0.5)?
Why is it U-shaped? What does it mean to have negative (-0.5) heads and tails? I don’t have an answer for this one yet. I even asked this on Stackexchange but haven’t gotten the response yet. If you have a good idea about the U-shaped Beta, please let me know!
Update: I ended up writing a blog post about it.