The motivation for not looking for interaction effects if there are no significant main effects is that one might end up comparing too many different models and could end up with the multiple comparisons problem. The scheme to only analyse interaction effects after main effects have been found is a way to reduce the probability for a false positive.
However, you can very well have a significant interaction without one or both main effects being significant.
Often, you have that the main effect correlates with the interaction effect and when the interaction is significant then the main effect will also be likely significant when we fit the model without the interaction, but this does not need to be the case. Here is an extreme example
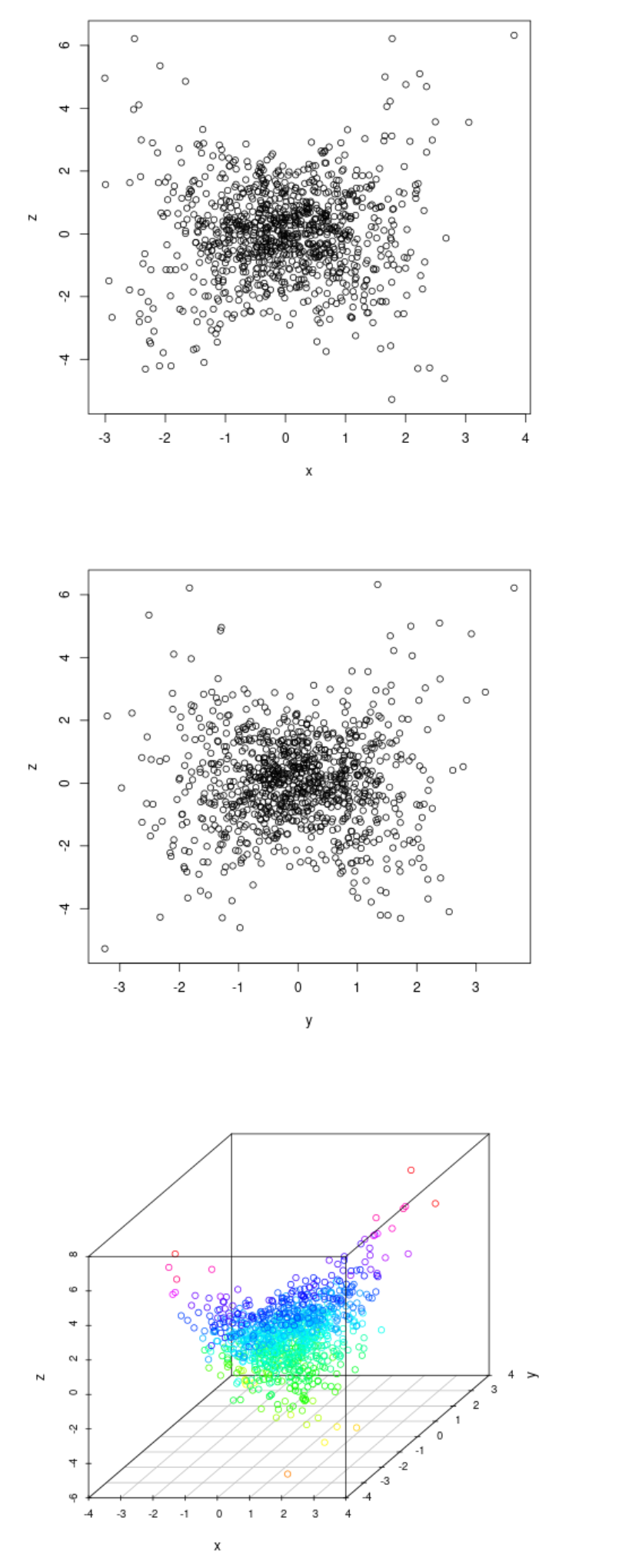
Let $$z = x \cdot y + \epsilon$$ with $x,y,\epsilon \sim N(0,1)$ This looks below
The variable $z$ when plotted versus $x$ or plotted versus $y$ is on average equal to $0$ independent from the value of $x$ or the value of $y$, and you will not find significant main effects.
But as a function of 'both' $x$ and $y$ and more specifically the product $x\cdot y$ you have a strong and clear effect.
In such a case it would be nonsense to ignore the interaction because there are no main effects.
Related question: One of the main effects not significant, but interaction term significant