I believe the easiest and most straightforward solution to your problem is to use a Bayesian analysis with non-informative prior assumptions as proposed by Gelman et al (2008). As Scortchi mentions, Gelman recommends to put a Cauchy prior with meanmedian 0.0 and scale 2.5 on each coefficient (normalized to have mean 0.0 and a SD of 0.5). This will regularize the coefficients and pull them just slightly towards zero. In this case it is exactly what you want. Due to having very wide tails the Cauchy still allows for large coefficients (as opposed to the short tailed Normal), from Gelman:
I believe the easiest and most straightforward solution to your problem is to use a Bayesian analysis with non-informative prior assumptions as proposed by Gelman et al (2008). As Scortchi mentions, Gelman recommends to put a Cauchy prior with mean 0.0 and scale 2.5 on each coefficient (normalized to have mean 0.0 and a SD of 0.5). This will regularize the coefficients and pull them just slightly towards zero. In this case it is exactly what you want. Due to having very wide tails the Cauchy still allows for large coefficients (as opposed to the short tailed Normal), from Gelman:
I believe the easiest and most straightforward solution to your problem is to use a Bayesian analysis with non-informative prior assumptions as proposed by Gelman et al (2008). As Scortchi mentions, Gelman recommends to put a Cauchy prior with median 0.0 and scale 2.5 on each coefficient (normalized to have mean 0.0 and a SD of 0.5). This will regularize the coefficients and pull them just slightly towards zero. In this case it is exactly what you want. Due to having very wide tails the Cauchy still allows for large coefficients (as opposed to the short tailed Normal), from Gelman:
I believe the easiest and most straightforward solution to your problem is to use a Bayesian analysis with non-informative prior assumptions as proposed by Gelman et al (2008). As Scortchi mentions, Gelman recommends to put a Cauchy prior with mean 0.0 and scale 2.5 on each coefficient (normalized to have mean 0.0 and a SD of 0.5). This will regularize the coefficients and pull them just slightly towards zero. In this case it is exactly what you want. Due to having very wide tails the Cauchy still allows for large coefficients (as opposed to the short tailed Normal), from Gelman:
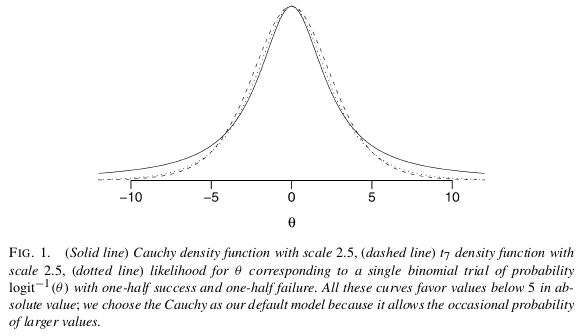
How to run this analysis? Why not useUse the bayesglm function in arm package that implements this analysis?!
fit <- bayesglm(y ~ x1 + x2, data=d, family="binomial") summarydisplay(fit) ## Call: ## bayesglm(formula = y ~ x1 + x2, family = "binomial", data = d) ## ## Deviance Residuals: ## Min 1Q Median 3Q Max ## -1.0312 -0.3827 -0.0348 0.4447 0coef.9993 ## ## Coefficients: ## Estimateest Stdcoef. Error z value Pr(>|z|) se ## (Intercept) -1.086110 1.0330 -1.051 0.29337 ## x1 -0.5785 0.855205 -0.676 0.49979 ## x2 3.6235 75 1.9187 1.889 85 0.059 . ## --- ## Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 ## ## (Dispersion parameter for binomial familyn taken= to10, bek 1) ##= 3 ## Nullresidual deviance: 13.863 on 9 degrees of= freedom ##2.2, Residualnull deviance: = 3.636 on 10 degrees of3 freedom ##(difference AIC:= 91.636 ## ## Number of Fisher Scoring iterations: 571) I believe the easiest and most straightforward solution to your problem is to use a Bayesian analysis with non-informative prior assumptions as proposed by Gelman et al (2008). How? Why not use the bayesglm function in arm package that implements this analysis?
fit <- bayesglm(y ~ x1 + x2, data=d, family="binomial") summary(fit) ## Call: ## bayesglm(formula = y ~ x1 + x2, family = "binomial", data = d) ## ## Deviance Residuals: ## Min 1Q Median 3Q Max ## -1.0312 -0.3827 -0.0348 0.4447 0.9993 ## ## Coefficients: ## Estimate Std. Error z value Pr(>|z|) ## (Intercept) -1.0861 1.0330 -1.051 0.293 ## x1 -0.5785 0.8552 -0.676 0.499 ## x2 3.6235 1.9187 1.889 0.059 . ## --- ## Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 ## ## (Dispersion parameter for binomial family taken to be 1) ## ## Null deviance: 13.863 on 9 degrees of freedom ## Residual deviance: 3.636 on 10 degrees of freedom ## AIC: 9.636 ## ## Number of Fisher Scoring iterations: 57 I believe the easiest and most straightforward solution to your problem is to use a Bayesian analysis with non-informative prior assumptions as proposed by Gelman et al (2008). As Scortchi mentions, Gelman recommends to put a Cauchy prior with mean 0.0 and scale 2.5 on each coefficient (normalized to have mean 0.0 and a SD of 0.5). This will regularize the coefficients and pull them just slightly towards zero. In this case it is exactly what you want. Due to having very wide tails the Cauchy still allows for large coefficients (as opposed to the short tailed Normal), from Gelman:

How to run this analysis? Use the bayesglm function in arm package that implements this analysis!
fit <- bayesglm(y ~ x1 + x2, data=d, family="binomial") display(fit) ## bayesglm(formula = y ~ x1 + x2, family = "binomial", data = d) ## coef.est coef.se ## (Intercept) -1.10 1.37 ## x1 -0.05 0.79 ## x2 3.75 1.85 ## --- ## n = 10, k = 3 ## residual deviance = 2.2, null deviance = 3.3 (difference = 1.1) This is an expansion of Scortchi and Manoel's answers, but since you seem to use R I thoughthought I'd supply some code. :)
I believe the easiest and most straight forwardstraightforward solution to your problem is to use a Bayesian analysis with non-informative prior assumptions as proposed by Gelman et al (2008). How? Why not use the bayesglm function in arm package that implements this analysis?
Super simple-simple, no?
This is an expansion of Scortchi and Manoel's answers, but since you seem to use R I though I'd supply some code. :)
I believe the easiest and most straight forward solution to your problem is to use a Bayesian analysis with non-informative prior assumptions as proposed by Gelman et al (2008). How? Why not use the bayesglm function in arm package that implements this analysis?
Super simple, no?
This is an expansion of Scortchi and Manoel's answers, but since you seem to use R I thought I'd supply some code. :)
I believe the easiest and most straightforward solution to your problem is to use a Bayesian analysis with non-informative prior assumptions as proposed by Gelman et al (2008). How? Why not use the bayesglm function in arm package that implements this analysis?
Super-simple, no?
