4
$\begingroup$

I am running a two-way repeated measures ANOVA (main effects: Time, Condition). The result is that the main effect of time is significant (P<0.05), the main effect of condition is not significant (P>0.05), and the interaction effect (time*condition) is significant (P<0.05).

Considering there is a significant interaction effect, we have ran Tukey post hoc testing to decompose the data points at each time and determine if differences exist. Although to my understanding this is acceptable, our approach has recently been questioned as an individual has suggested you need all main effects to be significant prior to further investigation into the significant interaction effect.

Does anyone have any thoughts/articles that may support/refute my approach. Kind regards,

Improve this question
$\endgroup$
0

4 Answers 4

Reset to default
11
$\begingroup$

Inadvertently, you're comparing apples and oranges. Once an interaction is included in the model, the interpretation of the main effect changes. With the interaction, the main effect of "condition" is the expected difference at time 0, and the effect of time is the slope of time trend for the referent condition.

The most likely scenario explaining your finding here is that the interaction projects the difference and slope of these effects to 0 at the specific timepoint. It of course does not mean you should remove them from the model - the interaction effect will no longer be interpretable. In the example plot below, I show two trendlines for a continuous variable X for a binary factor W. When the interaction is included in the model, the X trend is significant but the W effect is no longer significant. That's because when X=0, the values of Y are exactly the same whether W=0 or 1. However, it's clear from the graphic that both W and X are "significant" variables in the sense that the response is strongly predicted by their inclusion in the model - specifically the interaction.

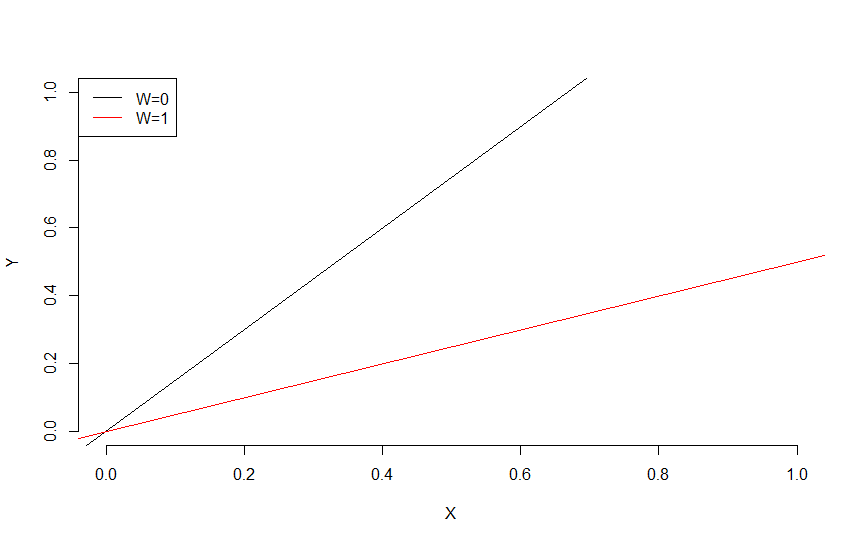
enter image description here

Improve this answer
$\endgroup$
4
  • 1
    $\begingroup$ This answer is broadly correct, but just to note that it can sometimes be appropriate to remove one or both of the base terms and retain the interaction, if there is a strong theoretical reason that the base terms have to be zero (usually more for experiments with chemicals, physics etc than with people --- you might think that a drug can't have an effect at time 0 before the chemicals have a chance to do anything, but there's the placebo effect to worry about). $\endgroup$ Commented Oct 27, 2022 at 8:44
  • 1
    $\begingroup$ @JDL this discussion is the same as "should the intercept term be removed when the trend line is known to intersect the origin?". I am team "no" because you increase the variance and bias of the slope term. $\endgroup$ Commented Oct 27, 2022 at 15:53
  • $\begingroup$ The trouble is, if you estimate the intercept as anything other than zero, the errors are no longer uncorrelated. Say you happen to estimate a positive value for the intercept; now errors for small X are more likely to be negative (you overestimated) and errors for large X are more likely to be positive (you underestimated). So the assumptions of Gauss-Markov are broken and the model with zero intercept is BLUE. $\endgroup$ Commented Oct 27, 2022 at 17:16
  • $\begingroup$ I think your comment holds true for a regression, but for ANOVA results do not depend on the reference group chosen, since comparison is wrt the grand mean, not a reference category: theanalysisfactor.com/… $\endgroup$ Commented Apr 26, 2023 at 15:01
7
$\begingroup$

If you have a significant interaction and you are using typical linear modeling, then the "main effects" represented by individual-predictor coefficients are at best hard to interpret and at worst outright confusing.

In the usual coding of predictors in R, what is typically taken to be the "main effect" for a categorical predictor like condition is its regression coefficient in a linear model. With an interaction in your situation, that is its association with outcome only when time = 0. That might be too early to see an association of condition with outcome if the conditions only differed starting at time = 0. See the plot in the answer from @AdamO, treating x as your time and w as your treatment.

The corresponding "main effect" for a continuous predictor like time would be its association with outcome when condition is at its reference level. If that reference level is "control" it's quite possible that you wouldn't have a "significant" "main effect" coefficient for time either, if the outcome is constant without an intervention.

The interaction coefficient tells you how much the association of time with outcome depends on the value of condition, and vice-versa. If that's appreciable (not even necessarily "significant"), the apparent "main effect" of one predictor can depend on the coding of a different predictor with which it interacts.

The best way to evaluate the importance of a predictor involved in an interaction requires evaluating all of the terms involving it, for example with likelihood-ratio tests or Wald tests on its sets of coefficients.

Finally, there's no requirement to do an initial ANOVA if you already planned to do all of the pairwise comparisons. So your Tukey pairwise comparisons are OK to perform in any case.

Improve this answer
$\endgroup$
4
  • 1
    $\begingroup$ Thank you @EdM for your extremely insightful responses to this issue. My understanding is that you support the approach I have used which is great. I am currently submitting this article for publication in an academic journal, and therefore, need a reference in order to support my approach to the reviewers. Are you aware of any resources that directly address my issue that I could cite? Thank you once again! $\endgroup$ Commented Oct 26, 2022 at 19:31
  • 2
    $\begingroup$ @ZacharyMcClean I happen to have this ancient text on hand. Section 16.2.2, page 180: "If the interaction effect is found to be significant, do not test the main effects even if they appear not to be significant. The estimation of the main effects and their significance is coding dependent when interactions are included in the model." Also, see this page and its links on whether you need to evaluate the significance of an initial ANOVA test when there are pre-planned comparisons. $\endgroup$ Commented Oct 26, 2022 at 21:28
  • $\begingroup$ Thank you @EdM I believe that this is perfect! $\endgroup$ Commented Oct 27, 2022 at 15:05
  • $\begingroup$ I think equivalence of the main effect with effect for the reference category holds true for a regression, but for ANOVA results do not depend on the reference group chosen, since comparison is wrt the grand mean, not a reference category: theanalysisfactor.com/… $\endgroup$ Commented Apr 26, 2023 at 15:03
4
$\begingroup$

The motivation for not looking for interaction effects if there are no significant main effects is that one might end up comparing too many different models and could end up with the multiple comparisons problem. The scheme to only analyse interaction effects after main effects have been found is a way to reduce the probability for a false positive.

However, you can very well have a significant interaction without one or both main effects being significant.

Often, you have that the main effect correlates with the interaction effect and when the interaction is significant then the main effect will also be likely significant when we fit the model without the interaction, but this does not need to be the case. Here is an extreme example

Let $$z = x \cdot y + \epsilon$$ with $x,y,\epsilon \sim N(0,1)$ This looks below

The variable $z$ when plotted versus $x$ or plotted versus $y$ is on average equal to $0$ independent from the value of $x$ or the value of $y$, and you will not find significant main effects.

But as a function of 'both' $x$ and $y$ and more specifically the product $x\cdot y$ you have a strong and clear effect.

In such a case it would be nonsense to ignore the interaction because there are no main effects.

example of no main effect

Related question: One of the main effects not significant, but interaction term significant

Improve this answer
$\endgroup$
1
  • 1
    $\begingroup$ Thank you to everyone who has commented on this post. Your expertise and advice were very helpful! $\endgroup$ Commented Oct 27, 2022 at 15:04
1
$\begingroup$

I am late to the party here, and there are already good answers. But I don't think the sentence:

an individual has suggested you need all main effects to be significant prior to further investigation into the significant interaction effect.

has been fully addressed (although it has been part of several answers, especially that of Sextus).

Sextus notes that exploring all interactions can lead to a lot of comparisons. That is certainly true.

However, I think the decision of whether to look at interactions, and which ones to look at, should be made before you run any other analyses and, ideally, before you gather data. Also, even if you decide, a priori to base it on some results, it should not be based on whether any effects are significant, but on the effect size.

It is possible to have both main effects be very close to 0 and yet have an interaction. This will happen, for instance, when a treatment has opposite effects in two groups.

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.