10
$\begingroup$

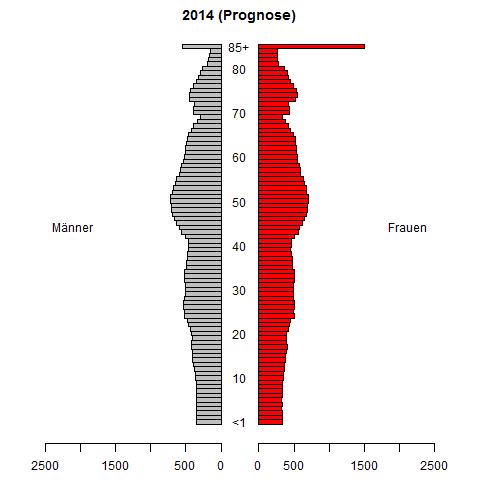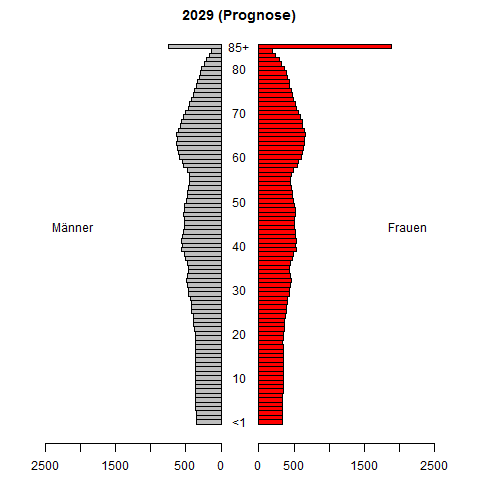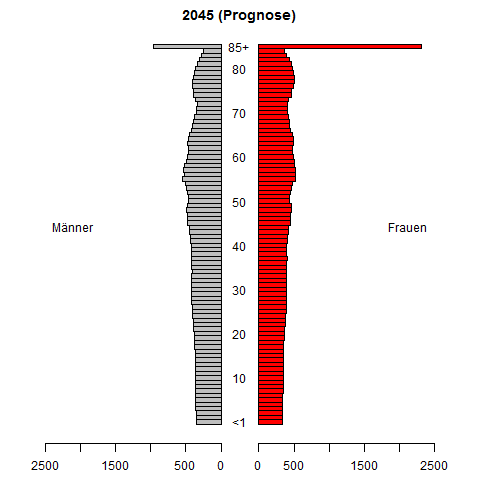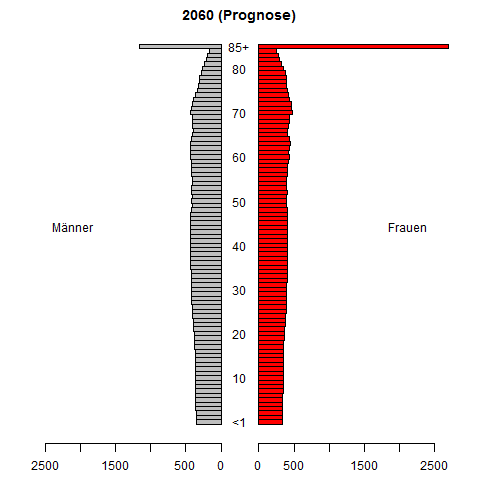
I am doing some research about forecasting time series of probability density functions. We are aiming to forecast a PDF given historically observed (usually, estimated) PDF. The forecasting method we are developing performs pretty well in simulation studies.

However, I need an numerical example from real applications to illustrate our method further. So, are there any proper examples in applications (finance, economics, biology, engineering, etc.) where a time series of PDFs are collected and it is important and difficult to forecast such a time series?

Improve this question
$\endgroup$
2
  • 1
    $\begingroup$ Try income distribution. It is certainly important to estimate it and forecast it. I would certainly be interested to see results. $\endgroup$ Commented Jul 1, 2013 at 10:49
  • 1
    $\begingroup$ The Bank of England releases density forecasts of inflation. You can find more info here: "Evaluating the Bank of England Density Forecasts of Inflation". Michael P. Clements The Economic Journal Vol. 114, No. 498 (Oct., 2004), pp. 844-866. $\endgroup$ Commented Feb 22, 2014 at 9:35

3 Answers 3

Reset to default
4
$\begingroup$

One important application lies in demographics, e.g., forecasting the development of age pyramids, which are really nothing but time-varying histograms, which in turn are density estimators. Try your approach on that.

Here are a few ideas about how to get longitudinal demographic density data. I finally went with the German dataset, which had the finest granularity, giving the annual pyramid in 1-year steps - most other datasets only binned each year's pyramid in 5-year-age bins. If you find a better source of demographic density time series, please tell us at that thread.

Hyndman and Shang (2009) is a paper on forecasting functional time series. They apply their method to fertility rates.

I'd also recommend the rainbow package for R also by Shang and Hyndman, for visualization of functional data.

Or you can visualize your forecasts using animations. Here is a little animated GIF I created for the future German population pyramid (men on the left, women on the right):

forecast

Improve this answer
$\endgroup$
1
$\begingroup$

There's a growing interdisciplinary literature on forecasting probability densities (as opposed to just forecasting the mean of a series). The following reference is a recent survey which discusses both methodology and applications in economics, meteorology, etc.

Gneiting, T. and M. Katzfuss (2014): "Probabilistic Forecasting", Annual Review of Statistics and Its Application 1, 125-151.

Available at http://www.annualreviews.org/doi/abs/10.1146/annurev-statistics-062713-085831

Improve this answer
$\endgroup$
1
  • $\begingroup$ The Gneiting and Katzfuss paper is a good one. However, the OP is not looking to forecast a predictive density from a time series of historically observed single data points. At each point in the past, he has observed a complete density. He is interested in forecasting how this entire density will evolve. Thus, this answer unfortunately misses the mark. $\endgroup$ Commented Nov 13, 2015 at 14:10
0
$\begingroup$

In fixed-income finance, you can observe the term structure time series of an asset. Concretely, for credit default swaps, how much you have to pay to get insured against a company's default for $t$ years. This price is directly linked to the probability of default of the company.

At instant $t=0$ the probability of default is $P(t=0) = 0$, at instant $t=\infty$ the probability of default is $P(t=\infty) = 1$, in between it is nondecreasing. You thus have a cumulative distribution function, and by derivation a probability density function. Since you can observe this curve on a daily basis, you have a time series of PDF which may have interesting dynamics.

Tell me if you are interested by a more detailed story about that.

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.