将二叉树转换为二叉搜索树
二叉树是一种非线性数据结构。它被称为二叉树,因为每个节点最多有两个子节点。这些子节点被称为左子和右子。它也可以解释为一个不定向图,其中最上面的节点称为根。二叉搜索树(BST)是一种具有特殊属性的二叉树,它有助于以排序的方式保持数据的组织。
在本教程中,我们将讨论如何将二叉树转换为二叉搜索树,同时保持二叉树的原始结构。
将二叉树转换为二叉搜索树的算法
-
创建一个名为
arr的数组来存储二叉树节点的顺序遍历。 -
使用任何排序算法(合并排序 O(nlogn)、快速排序 O(n^2)、插入排序 O(n^2)等)对
arr进行排序。 -
再次对树进行顺序遍历,并将排序数组
arr中的元素存储在二叉树中,得出 BST。
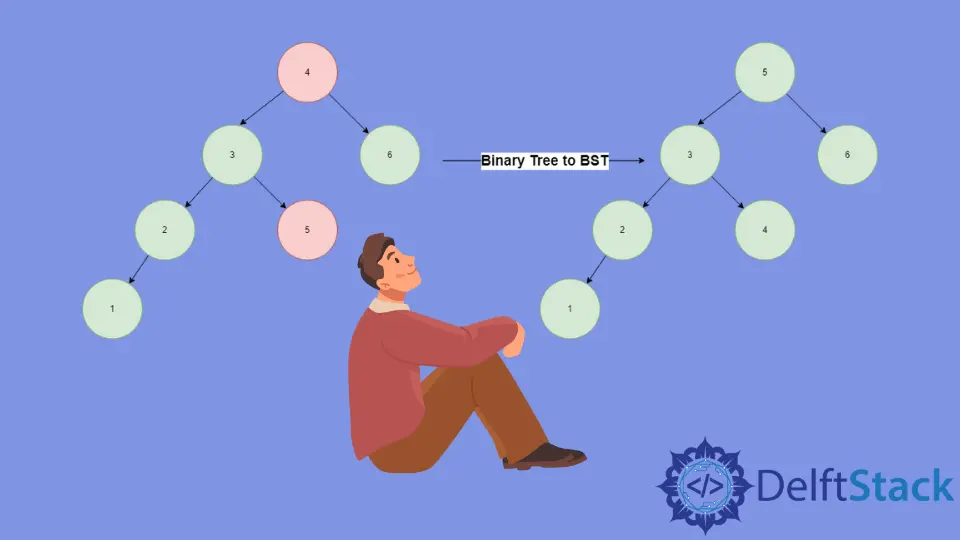
二叉树转换为 BST 图解
-
我们在根节点
4上调用顺序遍历。递归向左遍历到达节点1,它是最左的节点,并将其包含在我们的输出中;由于它是根节点,没有左节点,我们回溯到节点2,并将其包含在我们的遍历中。这样,我们遍历整棵树,并将按顺序遍历的结果以[1,2,3,5,4,6]的形式存储在数组arr中。 -
使用任意排序算法对数组
arr进行排序,得到[1,2,3,4,5,6]。 -
我们再次调用顺序遍历,将排序后的数组
arr存储回二叉树中,得到我们的 BST。
二叉树转换为二叉搜索树的实现
#include <bits/stdc++.h> using namespace std; class Node { public: int data; Node *left, *right; Node(int x) { this->data = x; this->left = this->right = NULL; } }; vector<int> v; void inorder(Node* root) { if (root != NULL) { inorder(root->left); cout << root->data << " "; inorder(root->right); } } void storetree(Node* root, int i = 0) { if (!root) { return; } storetree(root->left); v.push_back(root->data); storetree(root->right); } void restoretree(Node* root, int& i) { if (!root) { return; } restoretree(root->left, i); root->data = v[i]; i++; restoretree(root->right, i); } void converttoBST(Node* root) { if (!root) { return; } storetree(root); sort(v.begin(), v.end()); int i = 0; restoretree(root, i); } int main() { Node* root = new Node(3); root->left = new Node(1); root->right = new Node(7); root->left->left = new Node(4); root->left->right = new Node(5); root->left->left->right = new Node(2); root->right->left = new Node(6); root->right->right = new Node(9); root->right->right->left = new Node(8); cout << "The inorder traversal of the tree is : "; inorder(root); cout << endl; converttoBST(root); cout << "The inorder traversal of the tree is : "; inorder(root); cout << endl; } 将二叉树转换为 BST 算法的复杂度
时间复杂度
- 平均情况
我们将数组存储在 sorted 中,并将 sorted 数组存储回二叉树,进行无序遍历的时间复杂度为 O(n)。但是,对数组进行排序的复杂度是 O(nlogn),因此总复杂度给定为 O(nlogn)+2*O(n)。时间复杂度为 O(nlogn)。
- 最佳情况
最佳情况下的时间复杂度为 O(n)。当给定的二叉树已经是一个 BST 时,我们做无序遍历来实现它,而且不需要排序操作。
- 最坏情况
最坏情况下的时间复杂度为 O(nlogn)。
空间复杂度
由于递归调用所需的额外空间,该算法的空间复杂度为 O(n)。
Enjoying our tutorials? Subscribe to DelftStack on YouTube to support us in creating more high-quality video guides. Subscribe
作者: Harshit Jindal
Harshit Jindal has done his Bachelors in Computer Science Engineering(2021) from DTU. He has always been a problem solver and now turned that into his profession. Currently working at M365 Cloud Security team(Torus) on Cloud Security Services and Datacenter Buildout Automation.
LinkedIn
