Detect Cycle in a directed graph using colors
Last Updated : 23 Jul, 2025
Given a directed graph represented by the number of vertices V and a list of directed edges, determine whether the graph contains a cycle.
Your task is to implement a function that accepts V (number of vertices) and edges (an array of directed edges where each edge is a pair [u, v]), and returns true if the graph contains at least one cycle, otherwise returns false.
Example:
Input: V = 4, edges[][] = [[0, 1], [0, 2], [1, 2], [2, 0], [2, 3], [3, 3]]
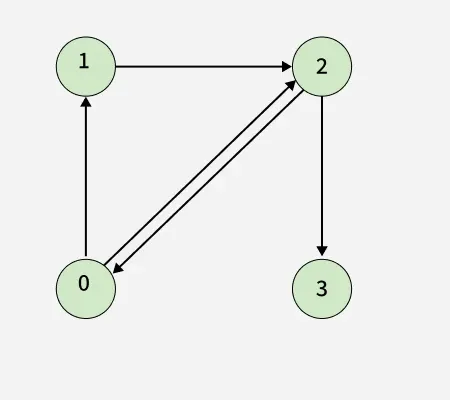 Cycle 0 → 2 → 0
Cycle 0 → 2 → 0 Output: true
Explanation: This diagram clearly shows a cycle 0 → 2 → 0
Input: V = 4, edges[][] = [[0, 1], [0, 2], [1, 2], [2, 0], [2, 3], [3, 3]]
 No Cycle
No CycleOutput: false
Explanation: The diagram clearly shows no cycle.
Understanding Back Edges in DFS and Their Role in Cycles
Depth-First Search (DFS) is a powerful technique that can be used to detect cycles in a directed graph. During a DFS traversal, if the graph is connected, it forms a DFS tree (or forest for disconnected graphs).
In such a tree, a cycle exists if and only if there is a back edge.
A back edge is an edge that points from a node to one of its ancestors in the DFS traversal this includes self-loops (an edge from a node to itself).
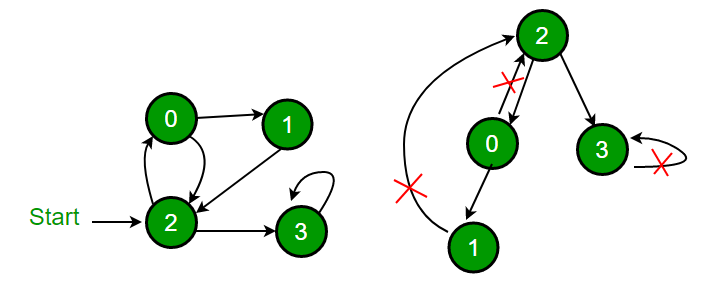
In the left graph, the DFS traversal begins from node 2, and during the traversal, several edges point back to nodes that are already in the current DFS call stack. These edges, marked with red ❌ symbols in the image, are known as back edges, and each one indicates the presence of a cycle in the graph. For example, the edge 3 → 3 is a self-loop, which forms a trivial cycle. The edge 2 → 0 connects to an ancestor in the DFS stack, creating a backward connection and thus a cycle. Similarly, the edge 1 → 2 completes a loop through multiple nodes, further confirming the existence of a cycle.
In the previous post, we have discussed a solution that stores visited vertices in a separate array which stores vertices of the current recursion call stack.
Approach:- Using Coloring - O(V+E) Time and O(V) Space
This algorithm solves the cycle detection problem in a directed graph by using Depth-First Search (DFS) with a coloring technique to track the state of each node during traversal. Nodes are marked as white(unvisited), gray (currently in the recursion stack), or black (fully processed). If during DFS we encounter a gray node, it means we’ve found a back edge—an edge pointing to a node still in the current DFS path—indicating a cycle. This method efficiently detects cycles by ensuring each node is visited once and each edge is checked once, resulting in a linear time solution relative to the size of the graph (O(V + E)).
Steps:
- Convert the edge list into an adjacency list for efficient traversal.
- Initialize Color Array, white
= 0 , gray = 1, black = 2 to track DFS state of each node. - Start dfs For every unvisited (white) node, start a DFS.
- Detect Back Edge in dfs, If you visit a gray node again → cycle exists.
- If any dfs finds a cycle, return
true; else, return false.
C++ #include <bits/stdc++.h> using namespace std; // Constructs an adjacency list for a directed graph vector<vector<int>> constructadj(int V, const vector<vector<int>> &edges) { vector<vector<int>> adj(V); for (const auto &edge : edges) { adj[edge[0]].push_back(edge[1]); } return adj; } // Utility function for DFS traversal and cycle detection // Uses coloring method to detect back edges bool dfsutil(int u, vector<vector<int>> &adj, vector<int> &color) { const int gray = 1, black = 2; // Mark the current node as being processed (gray) color[u] = gray; // Visit all neighbors for (int v : adj[u]) { // If the neighbor is also gray, we found a back edge -> cycle if (color[v] == gray) return true; // If the neighbor is unvisited (white), recur on it if (color[v] == 0 && dfsutil(v, adj, color)) return true; } // After processing all neighbors, mark the node as finished (black) color[u] = black; return false; } // Main function to detect cycle in a directed graph bool isCyclic(int V, const vector<vector<int>> &edges) { // Define color values locally: // 0 - white (unvisited), 1 - gray (visiting), 2 - black (visited) vector<int> color(V, 0); // Build the adjacency list from edge list vector<vector<int>> adj = constructadj(V, edges); // Perform DFS from every unvisited node for (int i = 0; i < V; ++i) { if (color[i] == 0) { if (dfsutil(i, adj, color)) return true; } } return false; } // Driver code to test the implementation int main() { int V = 4; vector<vector<int>> edges = {{0, 1}, {0, 2}, {1, 2}, {2, 0}, {2, 3}, {3, 3}}; cout << (isCyclic(V, edges) ? "true" : "false") << endl; return 0; } import java.util.*; public class GfG { // Constructs an adjacency list for a directed graph static List<Integer>[] constructadj(int V, int[][] edges) { List<Integer>[] adj = new ArrayList[V]; for (int i = 0; i < V; i++) { adj[i] = new ArrayList<>(); } for (int[] edge : edges) { adj[edge[0]].add(edge[1]); } return adj; } // Utility function for DFS traversal and cycle // detection static boolean dfsutil(int u, List<Integer>[] adj, int[] color) { final int gray = 1, black = 2; color[u] = gray; for (int v : adj[u]) { if (color[v] == gray) // back edge found return true; if (color[v] == 0 && dfsutil(v, adj, color)) // visit unvisited return true; } color[u] = black; return false; } // Main function to detect cycle in a directed graph static boolean isCyclic(int V, int[][] edges) { int[] color = new int[V]; List<Integer>[] adj = constructadj(V, edges); for (int i = 0; i < V; i++) { if (color[i] == 0) { if (dfsutil(i, adj, color)) return true; } } return false; } public static void main(String[] args) { int V = 4; int[][] edges = { { 0, 1 }, { 0, 2 }, { 1, 2 }, { 2, 0 }, { 2, 3 }, { 3, 3 } }; System.out.println(isCyclic(V, edges) ? "true" : "false"); } } # Constructs an adjacency list for a directed graph def constructadj(V, edges): adj = [[] for _ in range(V)] for u, v in edges: adj[u].append(v) return adj # Utility function for DFS traversal and cycle detection def dfsutil(u, adj, color): gray = 1 black = 2 color[u] = gray for v in adj[u]: if color[v] == gray: # Back edge found return True if color[v] == 0 and dfsutil(v, adj, color): # Visit unvisited node return True color[u] = black return False # Main function to detect cycle in a directed graph def isCyclic(V, edges): # 0 - white (unvisited), 1 - gray (visiting), 2 - black (visited) color = [0] * V adj = constructadj(V, edges) for i in range(V): if color[i] == 0: if dfsutil(i, adj, color): return True return False # Driver code V = 4 edges = [[0, 1], [0, 2], [1, 2], [2, 0], [2, 3], [3, 3]] print("true" if isCyclic(V, edges) else "false") using System; using System.Collections.Generic; class GfG { // Constructs an adjacency list for a directed graph static List<int>[] constructAdj(int V, int[, ] edges) { var adj = new List<int>[ V ]; for (int i = 0; i < V; i++) adj[i] = new List<int>(); int edgeCount = edges.GetLength(0); for (int i = 0; i < edgeCount; i++) { int from = edges[i, 0]; int to = edges[i, 1]; adj[from].Add(to); } return adj; } // Utility function for DFS traversal and cycle // detection static bool dfsutil(int u, List<int>[] adj, int[] color) { const int gray = 1, black = 2; color[u] = gray; foreach(int v in adj[u]) { if (color[v] == gray) return true; if (color[v] == 0 && dfsutil(v, adj, color)) return true; } color[u] = black; return false; } // Main function to detect cycle in a directed graph static bool isCyclic(int V, int[, ] edges) { int[] color = new int[V]; // 0 - white (unvisited), 1 - gray // (visiting), 2 - black (visited) var adj = constructAdj(V, edges); for (int i = 0; i < V; i++) { if (color[i] == 0) { if (dfsutil(i, adj, color)) return true; } } return false; } static void Main() { int V = 4; int[, ] edges = new int[, ] { { 0, 1 }, { 0, 2 }, { 1, 2 }, { 2, 0 }, { 2, 3 }, { 3, 3 } }; Console.WriteLine(isCyclic(V, edges) ? "true" : "false"); } } // Constructs an adjacency list for a directed graph function constructAdj(V, edges) { const adj = Array.from({length : V}, () => []); for (const [u, v] of edges) { adj[u].push(v); } return adj; } // Utility function for DFS traversal and cycle detection function dfsutil(u, adj, color) { const gray = 1, black = 2; color[u] = gray; // mark as visiting for (const v of adj[u]) { if (color[v] === gray) return true; // found a back edge (cycle) if (color[v] === 0 && dfsutil(v, adj, color)) return true; // visit unvisited node } color[u] = black; // mark as visited return false; } // Main function to detect cycle in a directed graph function isCyclic(V, edges) { const color = Array(V).fill(0); // 0 - white (unvisited) const adj = constructAdj(V, edges); for (let i = 0; i < V; i++) { if (color[i] === 0 && dfsutil(i, adj, color)) { return true; } } return false; } // Driver code const V = 4; const edges = [ [ 0, 1 ], [ 0, 2 ], [ 1, 2 ], [ 2, 0 ], [ 2, 3 ], [ 3, 3 ] ]; console.log(isCyclic(V, edges) ? "true" : "false"); Time complexity: O(V + E), where V is the number of vertices and E is the number of edges in the graph.
Space Complexity: O(V), Since an extra color array is needed of size V.
We do not count the adjacency list in auxiliary space as it is necessary for representing the input graph.
Detect Cycle in a Directed graph using colors
Explore
DSA Fundamentals
Data Structures
Algorithms
Advanced
Interview Preparation
Practice Problem