Absolute Deviation and Absolute Mean Deviation using NumPy | Python

To measure spread out of data values in a dataset we use Absolute Deviation and Absolute Mean Deviation. They help us understand how far each data point lies from a central value, usually the mean or median.

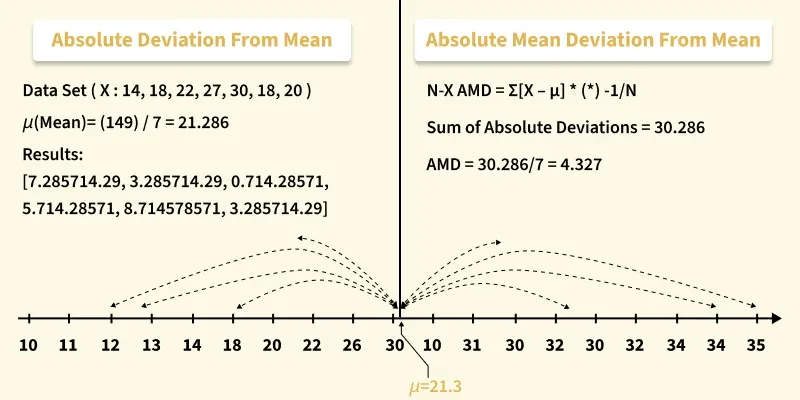Absolute Deviation

Absolute deviation is the distance between each data point and a central tendency, calculated without considering negative signs. It is useful for understanding how individual values scatter around the mean or median.

The absolute deviation of the observations x_1, x_2, x_3, ..., x_n around A is defined as:

A D_i = |x_i - A|

Absolute Mean Deviation

Absolute Mean Deviation is the average of all absolute deviations in a dataset. It summarizes the overall spread with a single representative value. A higher Absolute Mean Deviation indicates greater variability, while a lower value shows more consistency.

The absolute deviation of the observations x_1, x_2, x_3, ..., x_n around mean or median A is defined as:

1. For Discrete Data (Ungrouped)

\text{D(A)} = \frac{1}{n} \sum_{i=1}^{n} \lvert x_i - A \rvert

2. For Continuous Data (Ungrouped)

\text{D(A)} = \frac{1}{n} \sum_{i=1}^{K} f_i \lvert x_i - A \rvert

Where: n = \sum_{i=1}^{K} f_i

3. For Discrete Data (Grouped)

\text{D(A)} = \frac{\sum_{i=1}^{K} f_i\,|x_i - A|}{\sum_{i=1}^{K} f_i}

Where:

• x: data values
• f: frequency

4. For Continuous Data (Grouped)

\text{D(A)} = \frac{\sum_{i=1}^{K} f_i\,|m_i - A|}{\sum_{i=1}^{K} f_i}

Where:

• 𝑚: class midpoint
• f: frequency

Implementation

Implementation of Absolute Deviation and Absolute Mean Deviation:

Sample Dataset

Sample dataset represented as a NumPy array.

import numpy as np data = np.array([14, 18, 22, 27, 30, 18, 20]) 

Absolute Deviation from Mean

Calculating absolute deviation from mean. The mean acts as a common central point for comparison.

mean = np.mean(data) absolute_deviation = np.abs(data - mean) print("Mean:", mean) print("Absolute Deviation:", absolute_deviation) 

Output:

Mean: 21.285714285714285

Absolute Deviation: [7.28571429 3.28571429 0.71428571 5.71428571 8.71428571 3.28571429

1.28571429]

Absolute Mean Deviation from Mean

Calculating absolute mean deviation from mean. Averaging the deviations gives a clear measure of spread.

absolute_mean_deviation = np.mean(absolute_deviation) print("Absolute Mean Deviation:", absolute_mean_deviation) 

Output:

Absolute Mean Deviation: 4.326530612244897

Absolute Deviation from Median

Calculating absolute deviation from median. The median provides better resistance against outliers.

median = np.median(data) absolute_deviation_median = np.abs(data - median) print("Median:", median) print("Absolute Deviation from Median:", absolute_deviation_median) 

Output:

Median: 20.0

Absolute Deviation from Median: [ 6. 2. 2. 7. 10. 2. 0.]

Absolute Mean Deviation from Median

Calculating absolute mean deviation from median. Result is often smaller because the median minimizes total deviation.

absolute_mean_deviation_median = np.mean(absolute_deviation_median) print("Absolute Mean Deviation (Median):", absolute_mean_deviation_median) 

Output:

Absolute Mean Deviation (Median): 4.142857142857143