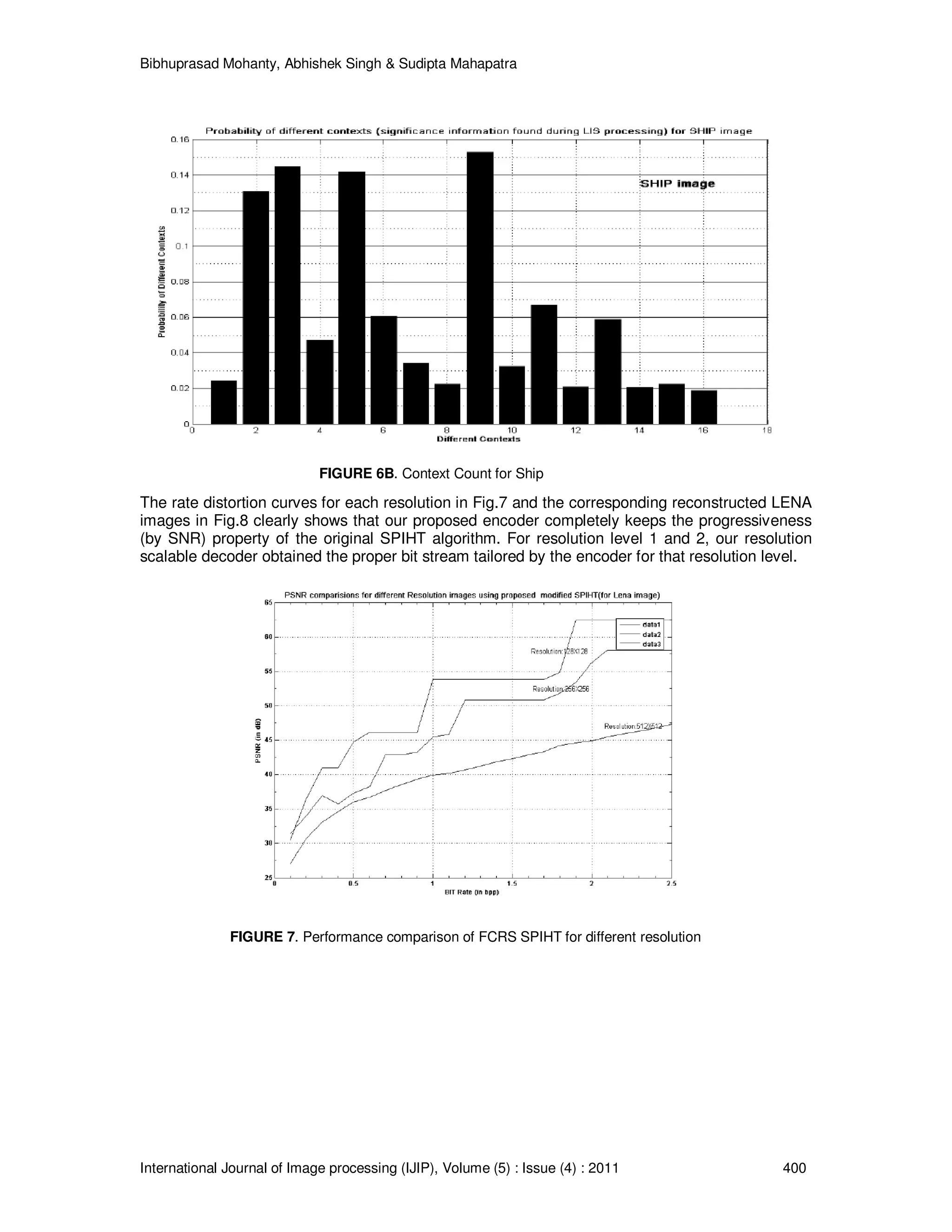
This paper introduces a modified SPIHT image compression technique that enhances spatial scalability and image quality through a zero-shifting pre-processing method and fixed context modeling. The proposed approach achieves improved performance in terms of encoding speed and quality, as measured by PSNR and SSIM, while maintaining compatibility with the SPIHT algorithm's embedded coding structure. The modifications allow for better handling of resolution scalability, enabling more efficient decoding across varying bandwidth and computation capabilities.
![Bibhuprasad Mohanty, Abhishek Singh & Sudipta Mahapatra International Journal of Image processing (IJIP), Volume (5) : Issue (4) : 2011 390 A High Performance Modified SPIHT for Scalable Image Compression Bibhuprasad Mohanty bmohanty.iit07@gmail.com. Assistant professor, Institute of Technical Education and Research SoA University, Bhubaneswar Abhishek Singh abhishek.uor@gmail.com. Assistant professor Faculty of Science and Technology, ICFAI University, Tripura Dr. Sudipta Mahapatra sudipta.mahapatra@gmail.com Associate Professor, Department of E &ECE, Indian Institute of Technology, Kharagpur, India Abstract In this paper, we present a novel extension technique to the Set Partitioning in Hierarchical Trees (SPIHT) based image compression with spatial scalability. The present modification and the preprocessing techniques provide significantly better quality (both subjectively and objectively) reconstruction at the decoder with little additional computational complexity. There are two proposals for this paper. Firstly, we propose a pre-processing scheme, called Zero-Shifting, that brings the spatial values in signed integer range without changing the dynamic ranges, so that the transformed coefficient calculation becomes more consistent. For that reason, we have to modify the initialization step of the SPIHT algorithms. The experiments demonstrate a significant improvement in visual quality and faster encoding and decoding than the original one. Secondly, we incorporate the idea to facilitate resolution scalable decoding (not incorporated in original SPIHT) by rearranging the order of the encoded output bit stream. During the sorting pass of the SPIHT algorithm, we model the transformed coefficient based on the probability of significance, at a fixed threshold of the offspring. Calling it a fixed context model and generating a Huffman code for each context, we achieve comparable compression efficiency to that of arithmetic coder, but with much less computational complexity and processing time. As far as objective quality assessment of the reconstructed image is concerned, we have compared our results with popular Peak Signal to Noise Ratio (PSNR) and with Structural Similarity Index (SSIM). Both these metrics show that our proposed work is an improvement over the original one. Key Words : Zero Shifting, 2D SPIHT, Lifting Wavelet Transform, Context Modeling, Resolution Scalability, SSIM 1. INTRODUCTION Image compression algorithms manipulate images to dramatically reduce the storage and bandwidth required while maximizing perceived image quality. Image compression based on discrete wavelet transform (DWT) has emerged as one of the popular tool. The wavelet domain provides a natural setting for many applications which involve real world signals. The presence of blocking artifacts at low bit rate in the entropy coding schemes (e.g., Discrete Cosine Transform) is completely avoided in this wavelet based coding. This transform achieves better energy compaction than the DCT and hence can help in providing better compression for the same quality measurement, like peak-signal-to-noise-ratio (PSNR) [1] and structural similarity (SSIM) [2].](https://image.slidesharecdn.com/ijip416-160212170631/75/A-High-Performance-Modified-SPIHT-for-Scalable-Image-Compression-1-2048.jpg)
![Bibhuprasad Mohanty, Abhishek Singh & Sudipta Mahapatra International Journal of Image processing (IJIP), Volume (5) : Issue (4) : 2011 391 The widespread deployment of diversified and heterogeneous digital networks requires different bandwidth range for various user nodes. This heterogeneity property demands for scalability to optimally serve each user according to the available bandwidth and computing capabilities. The goal of the scalable compression is to enable clients to reconstruct the image from a single compressed bit stream, according to their specific capabilities. A scalable coder generates a bit stream which consists of a set of embedded parts that offer better SNR and/or greater spatial resolution. Different types of decoders with different complexity and various access bandwidths can be accommodated in the case of an entirely scalable bit stream, Based on DWT, several competitive image compression coders with high coding efficiency have been developed. Among those coders, Shapiro’s Embedded Zero tree Wavelet (EZW) compression [3], Said and Pearlman’s set portioning in Hierarchical Trees (SPIHT) [4], and Tubman’s Embedded Block Coding with Optimized Truncation (EBCOT) [5] are the benchmark contribution. The 2-D SPIHT coder performs competitively with most of the other coders published in the literature [6]. The encoded and compressed SPIHT bit stream is further compressed by applying adaptive arithmetic encoder which provides an additional PSNR gain of 0.2 to 0.6 dB [4] over the original one. The low margin PSNR improvement shows the fact that SPIHT itself is exploiting the redundancies across the sub band so efficiently that it leaves little room for further compression by the arithmetic coder. However, use of arithmetic coder increases the computational complexity and hence the scheme sacrifices its speed for a meager gain. Further improvements of SPIHT have been published in [7-12]. In [13], the authors proposed a novel modification in exploiting the correlation of coefficients by lifting based DWT with 1D addressing method instead of traditional 2D method. Also, for the purpose of hardware implementation, they modified the SPIHT algorithm by interchanging the refinement pass and the sorting pass. Although almost all of the state-of-the-art zero tree-based image compression methods are SNR scalable and provide bit streams for progressive (by quality) image compression, they do not explicitly support spatial scalability and do not provide a bitstream which can be adapted easily to a heterogeneous environment. PROGRES [12] brings the concept of resolution scalability as well as faster encoding and decoding into the SPIHT, but it loses desirable feature like embeddedness and SNR scalable decoding. In this paper, we present a new scheme which provides significant improvement in the quality of the reconstructed image in terms of PSNR and SSIM without using the adaptive arithmetic encoder. The method, called zero shifting, is applied on the spatial domain of the image before it is wavelet transformed [18]. To accommodate the zero shifting schemes without sacrificing the inherent property of the SPIHT codec, we have modified the original algorithm in [4]. Further, we modeled the transformed coefficient according to its significance in a 2x2 adjacent offspring group as a fixed context. The systematic trend in probability distribution of such a context has been utilized for further compression of the image with the help of Huffman coding which is of lower complexity than the arithmetic coding [19]. We also propose an approach to resolution scalability by grouping together the bit streams generated for each resolution at one location. Both the sorting and refinement pass for SPIHT encoder is performed for each resolution and certain header information are generated which indicate the boundary condition for that resolution. The paper is organized as follows: Section 2 reviews the Lifting based wavelet transform and SPIHT coder briefly. The motivations for the proposed schemes are discussed in Section 3. The codec structure is described in Section 4 and we have discussed the results elaborately in Section 5. The conclusions of this paper are reported in Section 6. 2. BRIEF REVIEW 2.1Lifting Based Wavelet Transform (WT) Wavelet transforms provide both spatial and frequency-domain information about an image or a sequence of frames [14]. Such multiresolution representations of images/frames are often a more convenient format for image coding. This is particularly important since Human Vision System](https://image.slidesharecdn.com/ijip416-160212170631/75/A-High-Performance-Modified-SPIHT-for-Scalable-Image-Compression-2-2048.jpg)
![Bibhuprasad Mohanty, Abhishek Singh & Sudipta Mahapatra International Journal of Image processing (IJIP), Volume (5) : Issue (4) : 2011 392 (HVS) is less sensitive to high-frequency distortions than low-frequency ones. WT analyzes a signal at different frequency bands with different resolutions by decomposing it into a coarse approximation and detail information. The classical 2D transform is performed by two separate 1D transforms along the rows and the columns of the image data, resulting at each decomposition step in a low pass image or the coarse scale approximation, and three detail images. Because of their inherent multiresolution signal representation, wavelet-based coding schemes have the potential to support both SNR and spatial scalability [15]. The lifting scheme is a fast and efficient method to realize biorthogonal wavelet transforms [16]. It is simple, fast and reversible in computation due to the use of integer transformation. The algorithm has the advantages of using lifting, instead of convolution, which reduces the memory requirement. This influences the lossless compression algorithm profoundly because of its much wider dynamic range and hence JPEG 2000 uses the scheme. Even 3D wavelet decomposition is computed by applying three separate 1D transforms along the video data: rows and columns of the image as two directions and time as the third direction. 2.2Set Partitioning In Hierarchical Trees (SPIHT) SPIHT is an embedded coding technique. In embedded coding algorithms, encoding of the same signal at lower bit rate is embedded at the beginning of the bit stream for the target bit rate. Effectively, bits are ordered in importance. This type of coding is especially useful for progressive transmission using an embedded code; where an encoder can terminate the encoding process at any point. SPIHT algorithm is based on following concepts [4]: 1. Ordered bit plane progressive transmission. 2. Set partitioning sorting algorithm. 3. Spatial orientation trees. SPIHT keeps three lists: LIP, LSP, and LIS. LIP stores insignificant pixels, LSP stores significant pixels and LIS stores insignificant sets. At the beginning, LSP is empty, LIP keeps all coefficients in the lowest sub band, and LIS keeps all tree roots which are at the lowest sub band. SPIHT starts coding by running two passes. The first pass is the sorting pass. It first browses the LIP and moves all significant coefficients to LSP and outputs its sign. Then it browses LIS executing the significance information and following the partitioning sorting algorithms. The second pass is the refining pass. It browses the coefficients in LSP and outputs a single bit alone based on the current threshold. After the two passes are finished, the threshold is divided by 2 and the encoder executes the two passes again. This procedure is recursively applied until the number of output bits reaches the desired number. 3. THE PROPOSED SCHEME 3.1The Zero Shifting The method of zero shifting is a simple and easy-to-implement technique which preserves the embedded property of the SPIHT coding. By downward scaling of the pixel values by 2 (N-1) , N being the number of bits representing the original pixel, the spatial domain magnitude becomes bipolar ranging from (-2 (N-1) ) to (+2 (N-1) -1), with almost half of the maximum absolute spatial value. In the transform domain, the wavelet lifting scheme produces the high pass sub band by taking the weighted differences of the pixel values after prediction. Similarly, the low pass sub band is produced by taking the weighted average of the pixel values after the updating step. This low pass sub band is further decomposed iteratively for each level of decomposition to finally provide, one lowest frequency band, the rest being high frequency bands. SPIHT coding is a method of bit plane coding technique. The highest number bit plane is decided by the maximum absolute value of the transformed coefficients. As the maximum coefficient decreases by the method of zero shifting, SPIHT algorithm takes less time for encoding as well as for decoding. Further, the lower absolute image values in the spatial domain (which originally ranges from 0≤pi,j≤ 2N-1 ) are shifted to higher absolute range in the bipolar sense. The lower](https://image.slidesharecdn.com/ijip416-160212170631/75/A-High-Performance-Modified-SPIHT-for-Scalable-Image-Compression-3-2048.jpg)
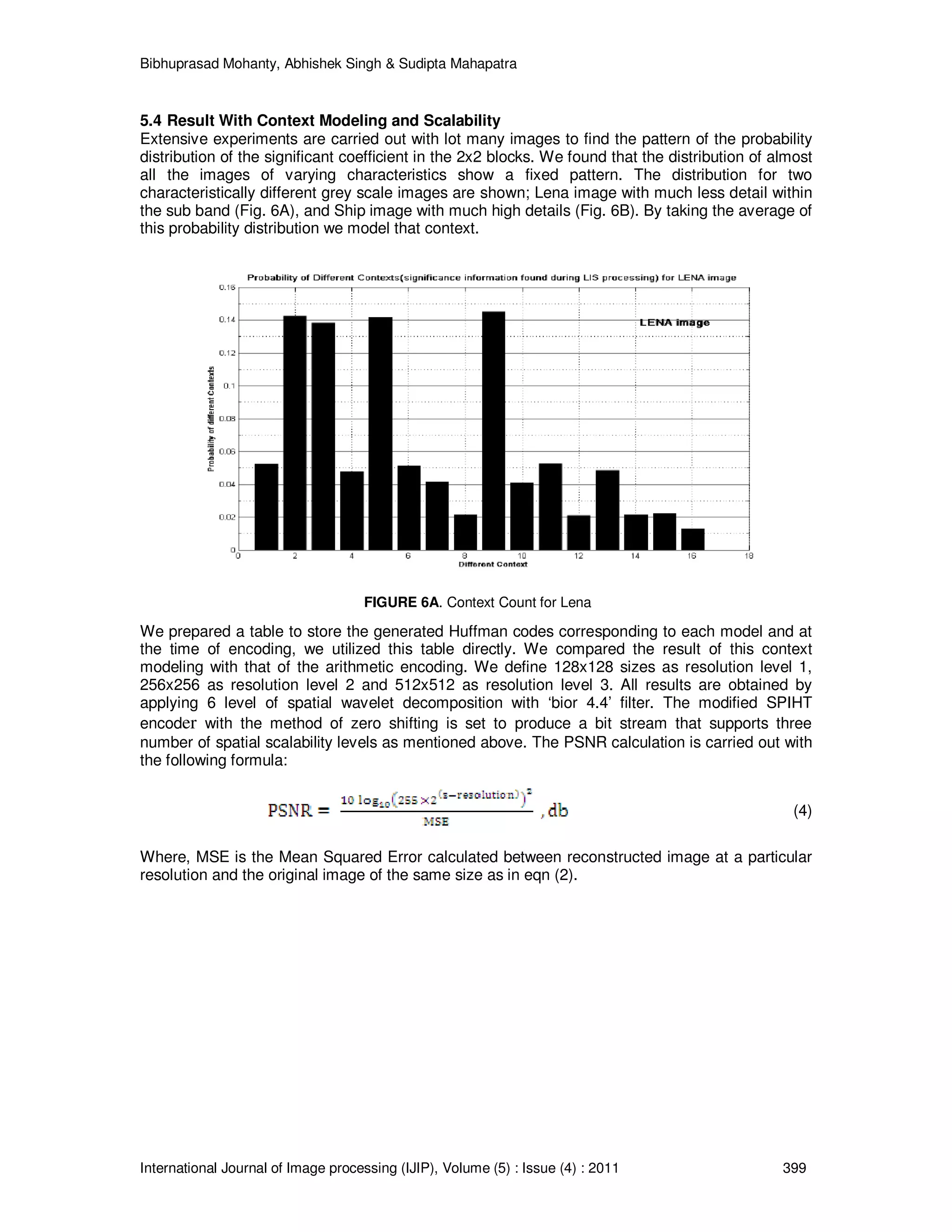
![Bibhuprasad Mohanty, Abhishek Singh & Sudipta Mahapatra International Journal of Image processing (IJIP), Volume (5) : Issue (4) : 2011 393 image values are detailed information pertaining to the boundaries, edges, etc. These coefficients become significant at a higher threshold value and accordingly are ordered earlier in the bit plane progressive transmission of the SPIHT bit stream. Since SPIHT algorithm always encodes a sign bit for significant coefficients, no extra bit budget is necessary for being bipolar. By terminating the decoding process even at a lower bit rate, the quality improves, both subjectively and objectively, because of the inclusion of some detail information at that rate. 3.2 Modified SPIHT The parent offspring dependency and corresponding spatial orientation trees for the SPIHT algorithm is as shown in Fig. 1 for three levels of decomposition. Each node of the tree is represented by its coordinates in the algorithm. The tree is defined in such a way that each node has no offspring (leaves) or four off springs at the same spatial location in the next finer level [4]. In original SPIHT, the pixels in the coarsest level e.g., LL sub band of the 3rd level for Fig. 1, are the tree roots and they are grouped into blocks of 2x2 adjacent pixels. In each block one (the left top corner) pixel has no descendant. In the initialization stage, the coordinates of all coefficients in the coarsest level are put into LIP list and the coordinates of coefficients having descendants only into the LIS list as D-type sets. We have modified the initialization stage of the SPIHT algorithm to accommodate the principle of zero shifting as follows: if the decomposition level is such that the coarsest level LL subband consists of a single pixel (e.g., for an image of 512x512 size decomposed into 9 level), then we set the LIS list with the HL, LH, and HH coordinates of the coarsest level (each of which is also a single pixel). Otherwise, we initialize the LIS list with all the coordinates of the LL sub band as of the LIP list. Accordingly, in the sorting pass for LIS, the SPIHT first tests the significance in the LH, HL, and HH band of the lowest subband. For each root in LL, it compares the maximum value between the other three bands at the same spatial orientation and sorts it in the output bit stream. Once this test is over, the set partition rule of SPIHT [6] divides the remaining descendants into either D-type set or L-type set. The decoder duplicates the path of execution of the encoder. At the encoder we are at a liberty to encode the entire bit plane without any bit budget constraint. Experiments carried out over different type of images with spatially different features show that the proposed modification provides a faster codec than the original one while resulting almost the same PSNR values. 3.3: Fixed Context Modeling SPIHT algorithm generates significant information during encoding of LIS and LIP. LIP is not supposed to generate any redundancies as they are distinctly decorrelated. When LIS of type A becomes significant at certain threshold, the significance information of offspring of 2x2 blocks are generated. We exploited the possibility of such four offspring being significant. Assigning 0 to insignificant and 1 to significant coefficient, we created 16 possible combination of such configuration, starting from 0000 to 1111. We called each configuration a context and found the probability of occurrence of each context model (Fig. 6A and 6B). The systematic trend found in FIGURE 1. Spatial Orientation tree in 2D SPIHT (source [8])](https://image.slidesharecdn.com/ijip416-160212170631/75/A-High-Performance-Modified-SPIHT-for-Scalable-Image-Compression-4-2048.jpg)

![Bibhuprasad Mohanty, Abhishek Singh & Sudipta Mahapatra International Journal of Image processing (IJIP), Volume (5) : Issue (4) : 2011 395 FIGURE 3. Proposed image codec with zero shifting In the decoder, the execution path of the encoder is duplicated and the values of inverse transformed coefficients are shifted upwards by 2 (N-1) to get back the original image. 5. RESULTS AND DISCUSSION 5.1Quality Measurement Metrics During the process of said compression, the reconstructed image is subject to a wide variety of distortion. Subjective evaluations emphasizes on the visual image quality, which is too inconvenient, time consuming, and complex. The objective image quality metrics like Peak Signal to Noise Ratio (PSNR), or Mean Squared Error (MSE) and structural Similarity (SSIM) [2] are thought to be the best for the image processing application. The MSE metric is most widely used for it is simple to calculate, having clear physical interpretation and mathematically convenient. MSE is computed by averaging the squared intensity difference of reconstructed image, and the original image, x. Then from it the PSNR is calculated. Mathematically, , (1) Where, MxN is the size of the image and assuming the grey scale image of 8 bits per pixel (bpp), the PSNR is defined as, (2) But, they are not very well matched to human visual perception. The authors in [2] have shown that even for the same PSNR values, the visual quality for two reconstructed images is different at different bit rate. It is because the pixels of the natural images are highly structured and exhibit strong dependencies. The SSIM system separates the task of similarity measurement into three comparisons: luminance, contrast, and structure. The overall similarity measure is defined as [2,17] (3) Where, x is the original assuming to be completely perfect and is the reconstructed image such that both are non negative images. S=1 implies a perfect similarity between the images. l(x, ) = luminance comparison function, which in turn the function of the mean values of x and ; c(x, ) = contrast comparison function and they are function of the standard deviation of x and ; and](https://image.slidesharecdn.com/ijip416-160212170631/75/A-High-Performance-Modified-SPIHT-for-Scalable-Image-Compression-6-2048.jpg)
![Bibhuprasad Mohanty, Abhishek Singh & Sudipta Mahapatra International Journal of Image processing (IJIP), Volume (5) : Issue (4) : 2011 401 (a) Resolution 1 (128x128) (b) Resolution 2 (256x256) (c) Resolution 3(512x512) FIGURE 8. FCRS reconstructed Lena at 0.5 bpp for 3 different level As expected, the performance of scalable decoder is much better than for SPIHT and as the resolution level becomes smaller (hence the scale becomes larger), the difference becomes more significant. All the results are obtained with the context modeling of the encoded bit stream. 6. CONCLUSION In this paper, we presented a novel extension of wavelet based SPIHT coding scheme. The scheme pre processed the pixel values around zero before any wavelet transform takes place. Higher PSNR and more compression are obtained with the scheme without using the popular arithmetic coding. Experimental results show that it performs better measurably and also at lower bit rate its performance is well suited for the purpose of surveillance and monitoring system. We have presented an extension to the original SPIHT by incorporating spatial scalability feature to the encoded bit stream. The bit stream can be stopped at any point to meet a bit budget during the process of coding and decoding for a particular resolution level. To lessen the burden of computation on the codec, we proposed a Huffman coding based context modeling to achieve further compression at each resolution level. This technique can be extended for combined SNR, spatial and frame rate scalable video coding. 7. REFERENCES [1] G. Wallace, “The JPEG still picture compression standard,” Communications of ACM, vol. 34, no. 4, 1991. [2] Z. Wang, A. C. Bovik, H. R. Sheikh, and E. P. Simoncelli, "Image quality assessment: From error visibility to structural similarity," IEEE Transactios on Image Processing, vol. 13, no. 4, pp. 600-612, Apr., 2004. [3] J.M. Shapiro, “Embedded image coding using Zero trees of wavelet coefficients,” IEEE Trans. on Signal Processing, vol.41, pp. 3445-3462, Dec.,1993. [4] A.Said and W.A.Perlman, “A New, Fast, and Efficient Image Codec Based on Set Partitioning in Hierarchical Trees,” IEEE Trans. on Circuits and Systems for Video Technology, vol.6, pp. 243-250, June, 1996.](https://image.slidesharecdn.com/ijip416-160212170631/75/A-High-Performance-Modified-SPIHT-for-Scalable-Image-Compression-12-2048.jpg)
![Bibhuprasad Mohanty, Abhishek Singh & Sudipta Mahapatra International Journal of Image processing (IJIP), Volume (5) : Issue (4) : 2011 402 [5] D. Taubman, “High Performance Scalable Image Compression with EBCOT ,” IEEE Trans. on Image Processing, vol. 9, pp. 1158-1170, July, 2000. [6] B.-J.Kim and W. A. Pearlman, “An embedded video coder using three-dimensional set partitioning in hierarchical trees (SPIHT),” in proc. IEEE Data Compression Conf., pp. 251– 260, Mar., 1997. [7] J. Karlenkar and U. B. Desai, “SPIHT video coder,” in Proc. IEEE Region 10 International Conference on Global Connectivity in Energy, Computer, Communication and Control, TENCON’98, vol. 1, pp. 45–48, 1998. [8] B.-J. Kim, Z. Xiong, and W. A. Pearlman, “Low bit-rate scalable video coding with 3-d set partitioning in hierarchical trees (3-D SPIHT),” IEEE Trans. Circ. and Syst. for Video Technology, vol. 10, no. 8, pp. 1374–1387, Dec. 2000. [9] J. Zho and S. Lawson, “Improvements of the SPIHT for image coding by wavelet transform,” Proc. IEEE Seminar on Time-scale and Time-Frequency Analysis and Applications (Ref. No. 2000/019), pp. 24/1 –24/5, 2000. [10] E. Khan and M. Ghanbari, “Very low bit rate video coding using virtual spiht,” IEE Electronics Letters, vol. 37, no. 1, pp. 40–42, Jan. 2001. [11] H. Cai and B. Zeng, “A new SPIHT algorithm based on variable sorting thresholds,” in Proc. IEEE Int. Symp. Circuits and Systems, vol. 5, pp. 231–234, May 2001. [12] Yushin Cho, W.A.Pearlman and A. Said, “Low complexity resolution progressive image coding algorithm: progres (progressive resolution decompression)”, IEEE International Conference on Image processing, Volume 3, pp. 49-52, 2005. [13] J.Jyotheswar and S. Mahapatra, “Efficient FPGA implementation of DWT and modified SPIHT for lossless image compression,” Journal of System Architecture, vol. 53, pp.369- 378, 2007. [14] S. Mallat, "A Theory for Multiresolution Signal Decomposition: The Wavelet Representation," IEEE Trans. Patt. Rec. and Mach. Int., Vol. PAMI-11, No. 7, pp. 2091-2110, July 1989. [15] J.R.Ohm, “Three dimensional subband coding with motion compensation,” IEEE Trans. Image Processing, vol.3, no. 5, pp. 559-571, Sept. 1994. [16] W. Sweldens,” The Lifting Scheme: A Custom-design Construction of Biothogonal Wavelets,” Journal of Applied Computation Haron Anal, vol.3, issue 2, pp. 186-200, 1996. [17] http://www.ece.uwaterloo.ca/~z70wang/research/ssim [18] B.Mohanty, P.Verma and S.Mahapatra, “A High Performance SPIHT based Image and Video codec for survelliance,” Int.journal of Signal and Imaging System Engg.(in press). [19] A. Singh, B. Mohanty, P. Verma and S. Mahapatra, “Fixed context resolution scalable SPIHT: a novel extension,” Proc. of International conference on Communication, Computation, Control and Nanotechnology (ICN 2010), pp. 28-32, Oct.2010.](https://image.slidesharecdn.com/ijip416-160212170631/75/A-High-Performance-Modified-SPIHT-for-Scalable-Image-Compression-13-2048.jpg)