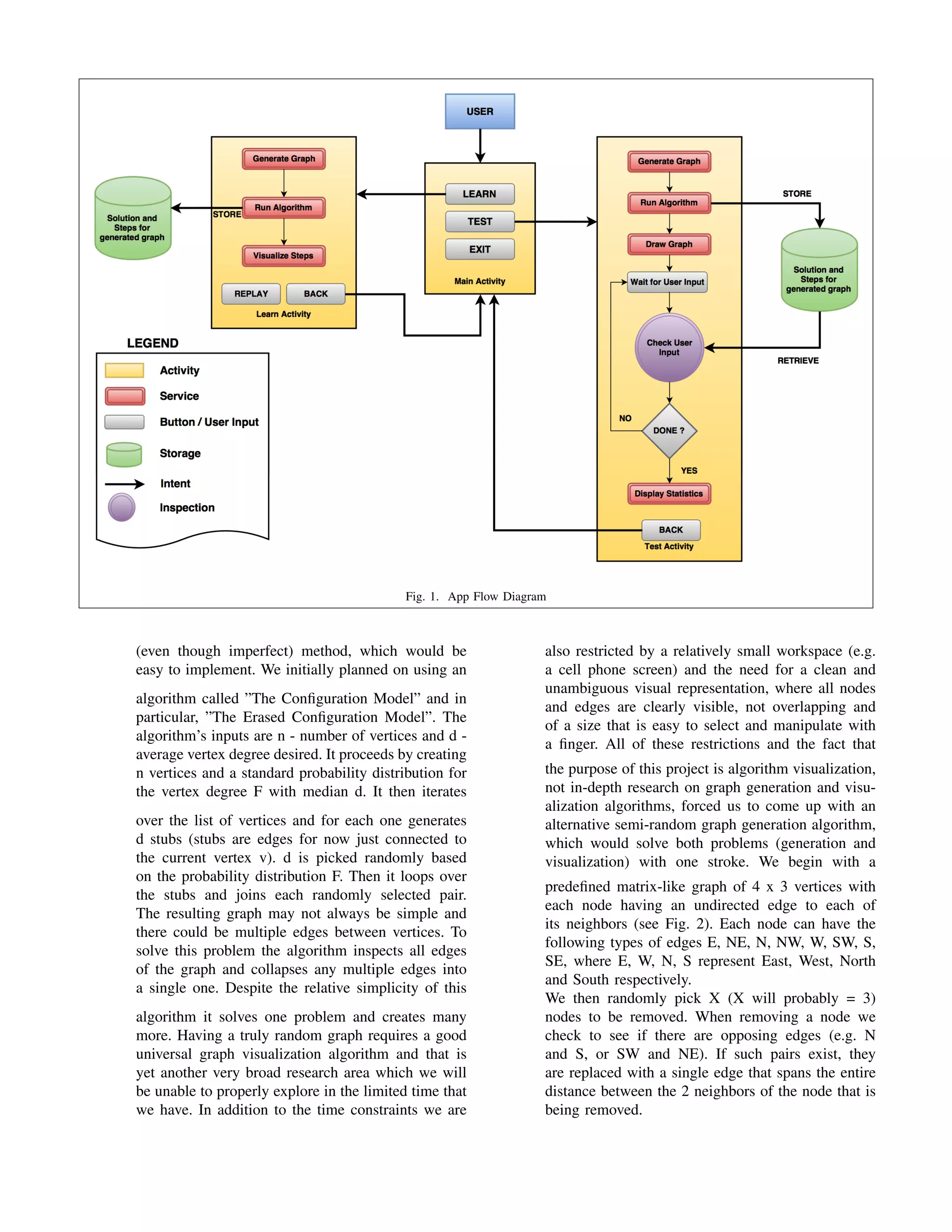
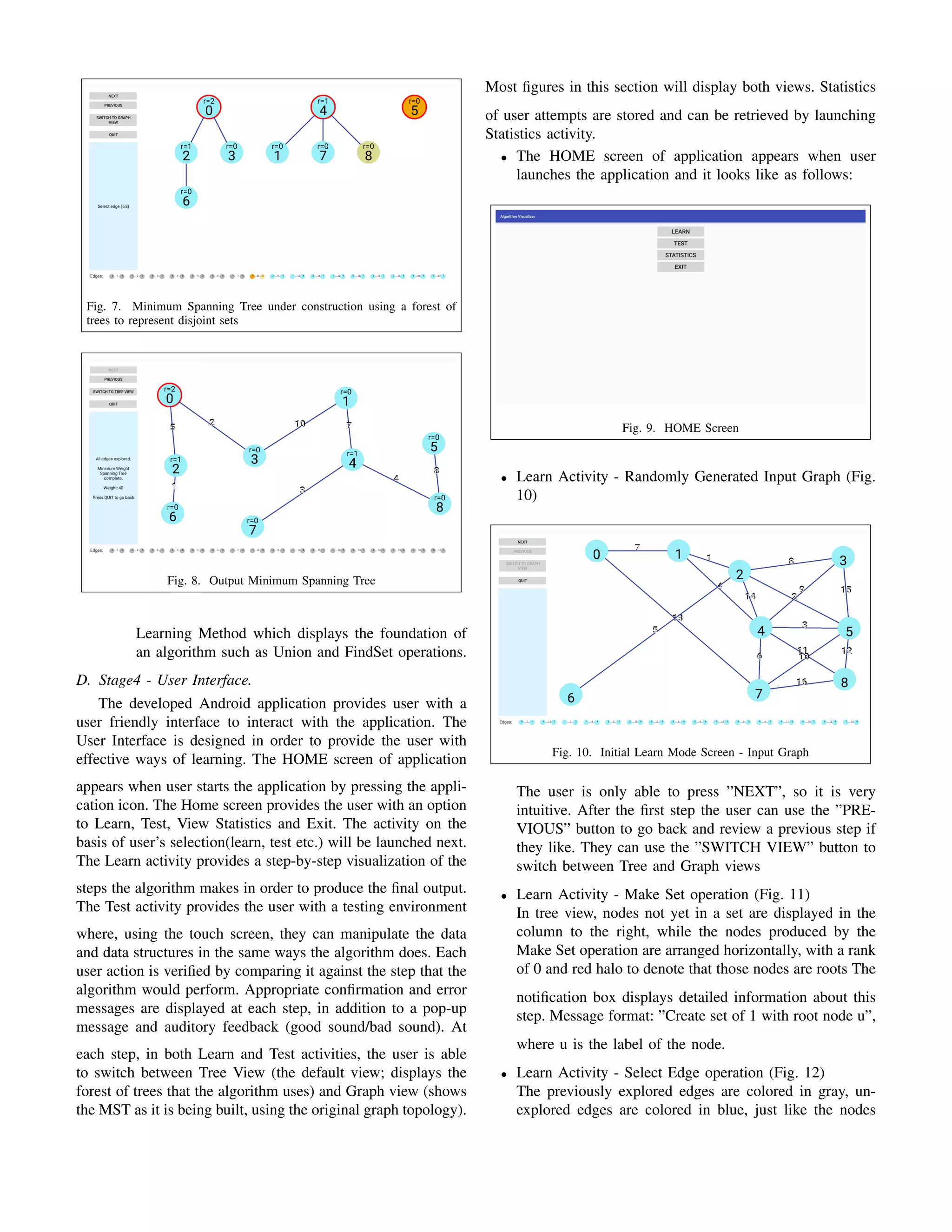
This document proposes an Android application to serve as an educational tool for visualizing algorithms and testing user knowledge. The application would have three main components: 1) A learning mode that visually demonstrates algorithms step-by-step; 2) A testing mode that allows users to manipulate data structures and verify their understanding; 3) Statistics on user errors to help instructors. The project aims to help students learn algorithms on mobile devices. It will focus on graph algorithms like Kruskal's minimum spanning tree and use randomly generated graphs for testing. The application will be developed in four stages: requirements gathering, design, infrastructure implementation, and user interface development.


![Fig. 2. Initial default graph with nodes marked for deletion Fig. 3. Nodes removed Finally we loop over all edges and assign them ran- dom weights from a pre-specified range. If the graph needs to be directed, we replace each undirected edge (u,v) with a random choice of either 1 directed edge (u, v), 1 directed edge (v, u) or 2 directed edges (u, v) and (v, u) - i.e. a loop (See Fig. 4). Even though quite simple this algorithm can still generate, a wide variety of graphs, sufficient for our needs and greatly simplifies the graph visualization problem, allowing us to spend more time on the user interface and experience. – Graph Generation Algorithm (Data Structures) Please note that since a lot of the data structures we use are shared between modules, we will only list their names and for more information you can refer to the comprehensive list of data structures at the end of this section. Pseudocode: Fig. 4. Cross edges removed. Directed graph. function generate graph(height, width) input height: the height of the base graph which will prune, the width of the base graph which will prune output: A random graph begin graph base = generate empty graph(height, width) for i := 0 to height for j := width boolean node lives = gener- ate random number(0, 1) > 0.5 ? true : false; if(node lives) base[i][j].valid = true; foreach (node1, node2) in base boolean edge lives = gener- ate random number(0, 1) > 0.5 ? true : false; if(edge lives) node1.connects(node2) return base; end Data structures used for graph generation: Graph, Node, Edge – Visualize Steps (Description) In order to be able to visualize (in learn mode) and verify (in test mode) steps, we store the steps that the selected algorithm takes during its execution and store them in an ordered list. Each step can be comprised of 1 or more actions. Here’s an example of a step with multiple actions: selectEdge(u, v), relaxNode(u, v, w); During visualization we begin by drawing the original graph. We then loop over the list of steps, executing each one and redrawing](https://image.slidesharecdn.com/cs512projectlatexreport-160906030902/75/Algorithm-Visualizer-4-2048.jpg)
![the graph. In addition to specifying what actions to take in each step, actions are also described in plain English and captions of each step are displayed, wherever applicable, each time the graph is redrawn. – Visualize Steps (Data Structures) Data structures used: Exercise, Graph, Node, Edge, SolutionStep, Action – Verify Steps (Description) The verification process is very similar to the step visualization process. After the original graph is displayed we wait for user input. We then wait for user input. When the user has made the same number of actions as the number of actions we have in the current step, we display a ”Confirm Step” button to the user. The user has the choice to make changes to the steps they have made or confirm. The total time taken by the user to execute this step is recorded for statistical purposes. Upon confirmation we compare the actions that the user made in the current step, with the actions we expect. Actions do not need to be in the same order, so for each user action we search the entire list of actions comprising the current step. If all steps match, the user is given positive feedback (ding sound) and is allowed to continue. If the user has made a mistake he is given negative feedback (buzzer sound) and is allowed to retry. If the user makes 3 mistakes the correct step is executed and visualized and the user is allowed to continue. – Verify Steps (Data Structures) Data structures used: Exercise, Graph, Node, Edge, SolutionStep, Action, Mistake, DBHandler – Draw Graph (Description) The graph generation algorithm provides us with a list of nodes and edges and has an inherently neat rectangular shape overall, so displaying the graph is quite trivial. We begin by first drawing the nodes. We know the screen size and node size relative to the screen size, margins and padding, as well as the number of rows and columns of nodes so it is easy to calculate the spacing between nodes. The edges of each node are also labeled using geographic directions so we know where each node needs to be positioned relative to others. Once the node positions for the current screen size are calculated (Fig. 4), we add some random jitter to their positions, in order to make the graph look more random and less rectangular. The jitter is a small translation in a random direction. The resulting graph now looks a lot more random and less artificial (Fig. 5). Pseudo code Function draw graph(nodes[row][col], edges, width, height) Fig. 5. Cross edges removed. Directed graph. input: nodes[row][col], edges, screen width, screen height begin node radius = min( (height - 100)/row, (width - 50)/col ); for i := 0 to row, for j := 0 to col, if(nodes[row][col] is set to show): X = 25 + col * (node radius + node padding); Y = 50 + row * (node radius + node padding); draw circle(node radius, X, Y); for each edge E, Nodes start = E.start Nodes end = E.end draw line(start.coordinates, end.coordinates) end – Verify Steps (Data Structures) Data structures used: Graph, Node, Edge – Display Statistics Upon completion of the exercise we loop through all the steps taken by the user and calculate the total number of mistakes made and time taken to complete the exercise. – Data Structures (Detailed Outline) Node (properties) ∗ label ∗ value ∗ color ∗ size ∗ border thickness ∗ position ∗ edges (E, NE, N, NW, W, SW, S, SE, Other)](https://image.slidesharecdn.com/cs512projectlatexreport-160906030902/75/Algorithm-Visualizer-5-2048.jpg)




![Fig. 19. User is advancing to next step automatically Fig. 20. User Test Trials Statistics. – Extendability and Usability: Add more algorithms and further improve the user experience. Currently in order to extend the app capabilities by adding an additional algorithm, the programmer would need to create a Java class with the algorithm implementa- tion, as well as create activities for the Learn and Test modes, where they implement a button for each possible algorithm action. This process is not easy to automate but it is possible to create a standardized way of doing this (e.g. a plugin architecture), so that algorithms can be added without the need to code in Java. – Global Statistics: Currently the statistics are stored in a SQLite3 database on each individual machine, so the data collected is for the users of that particular device only. The data can easily be stored in an online database. This improvement would allow a teacher to easily get statistics about multiple students at once. REFERENCES [1] Roberto Tamassia, Handbook of Graph Drawing and Visualization - https://cs.brown.edu/∼rt/gdhandbook/ [2] Force-Directed Graph Drawing Approach - https://en.wikipedia.org/ wiki/Force-directed graph drawing [3] Force-Directed Graph Drawing Approach - https://www.youtube.com/ watch?v=VxiKoT I P4 [4] JUNG - Java Universal Network/Graph Framework - http://jung. sourceforge.net/ [5] Flowchart Shape and What They Mean - http://www.rff.com/flowchart shapes.htm [6] 10 Tips and Tricks for Making Flowcharts - http://www.breezetree.com/ article generalflowcharting1.htm](https://image.slidesharecdn.com/cs512projectlatexreport-160906030902/75/Algorithm-Visualizer-11-2048.jpg)