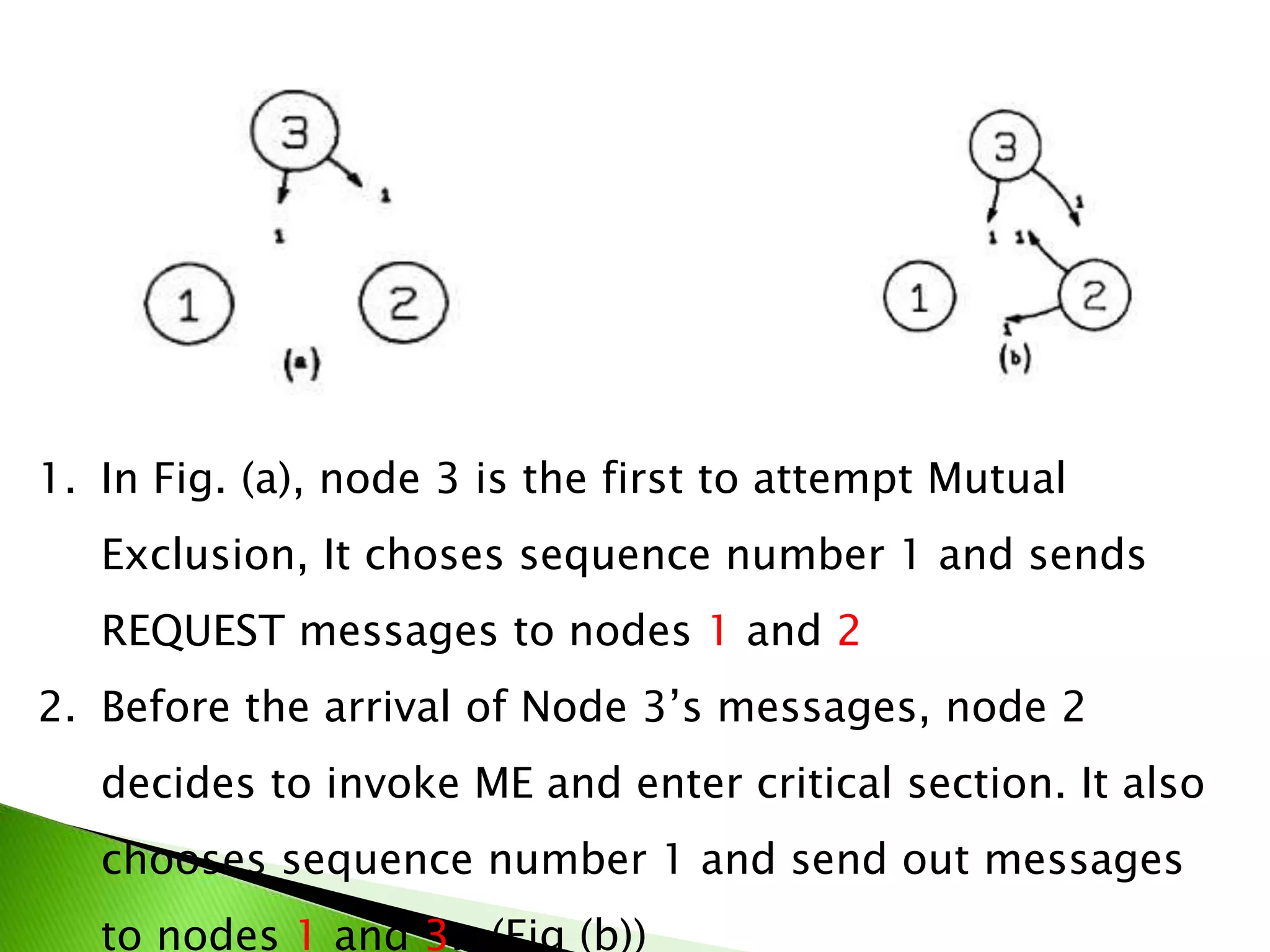
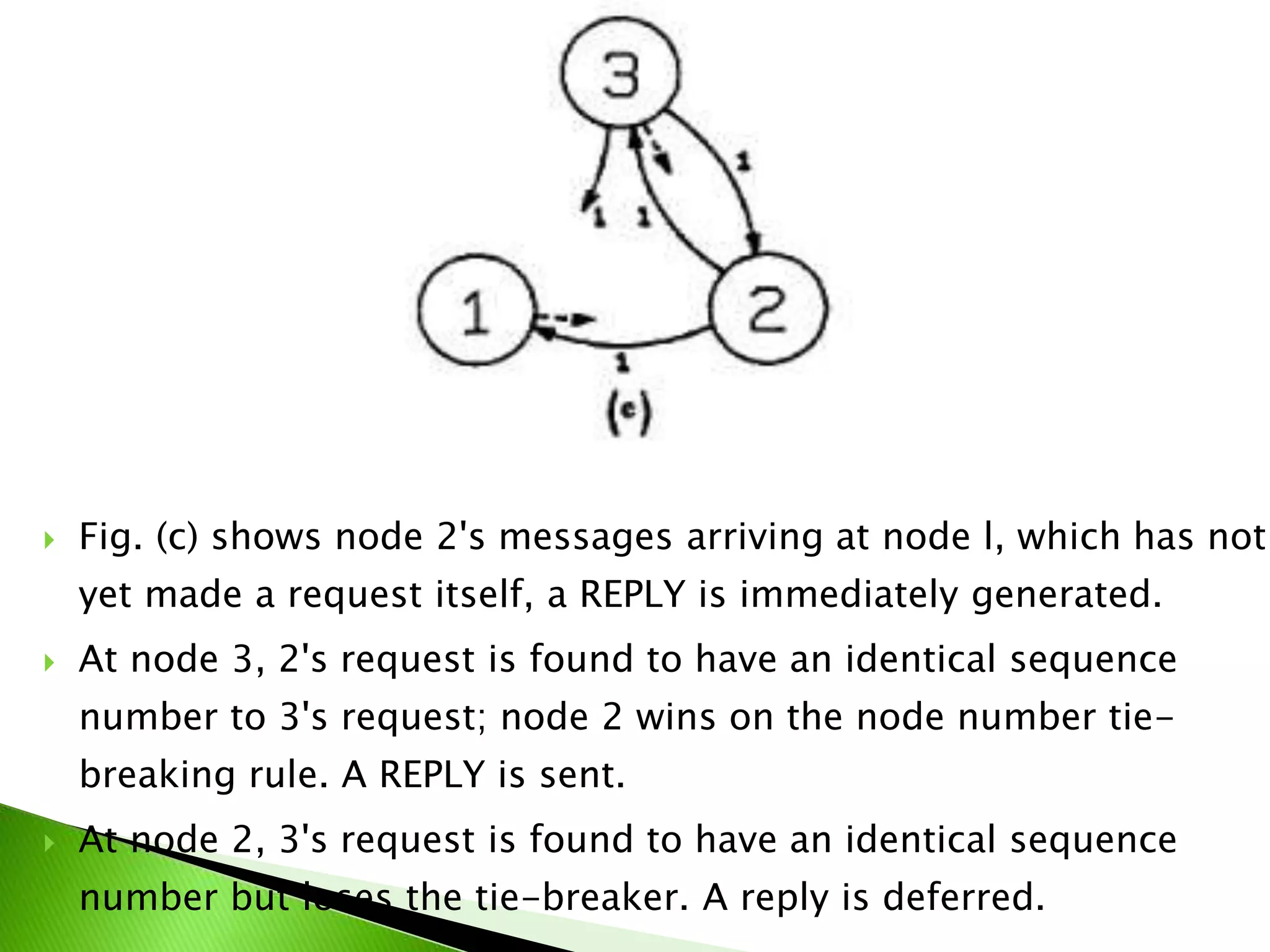
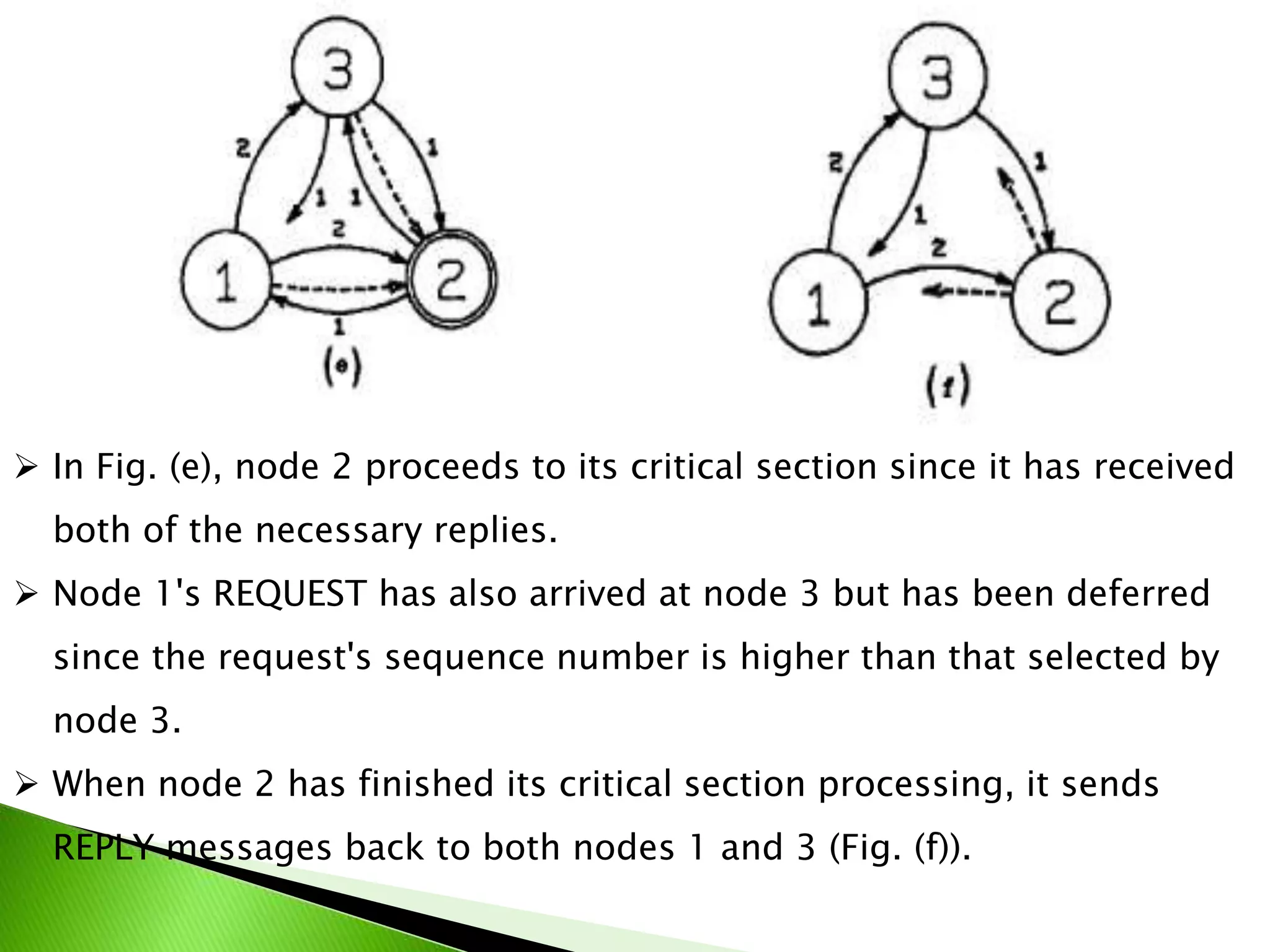
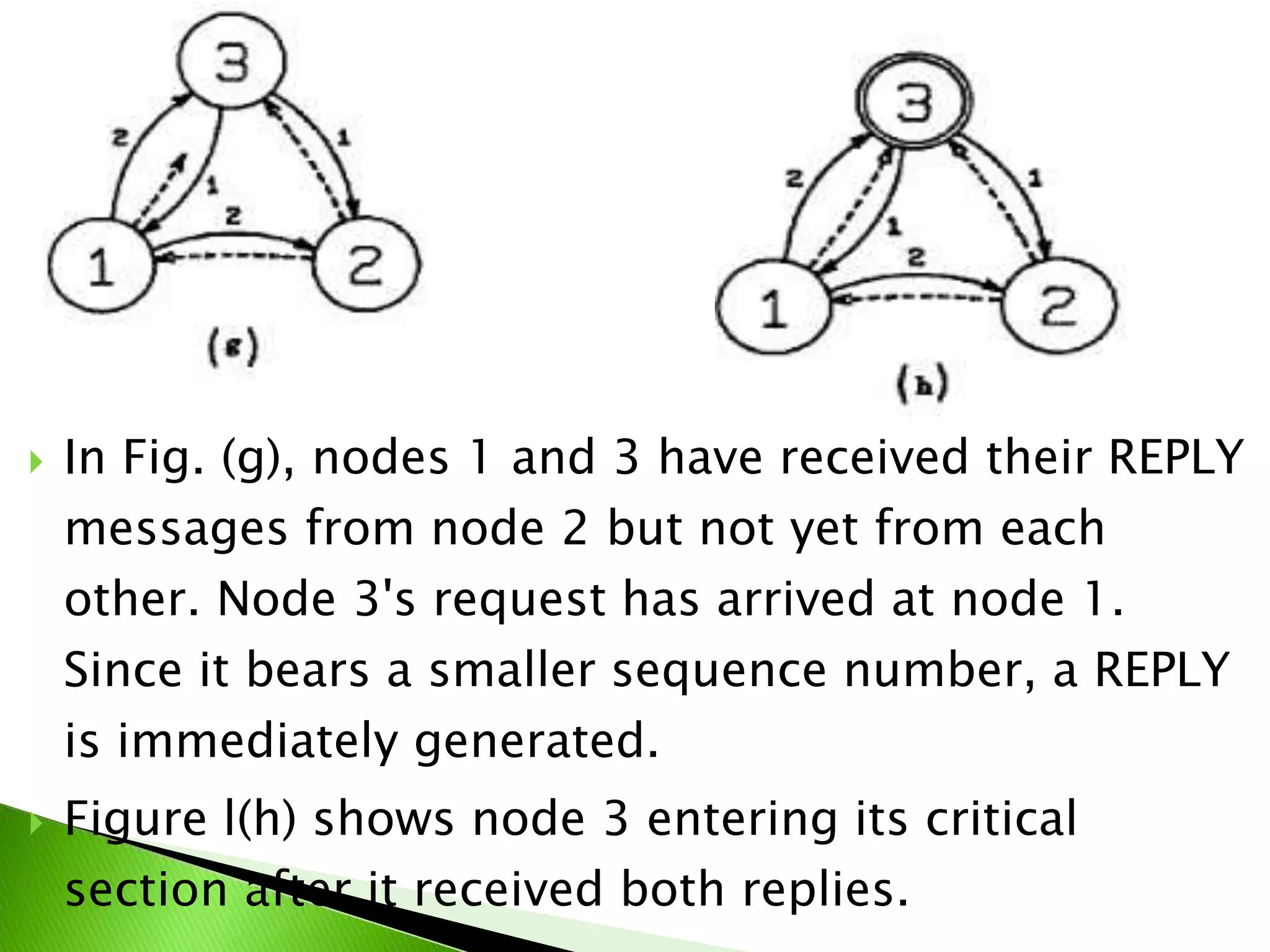
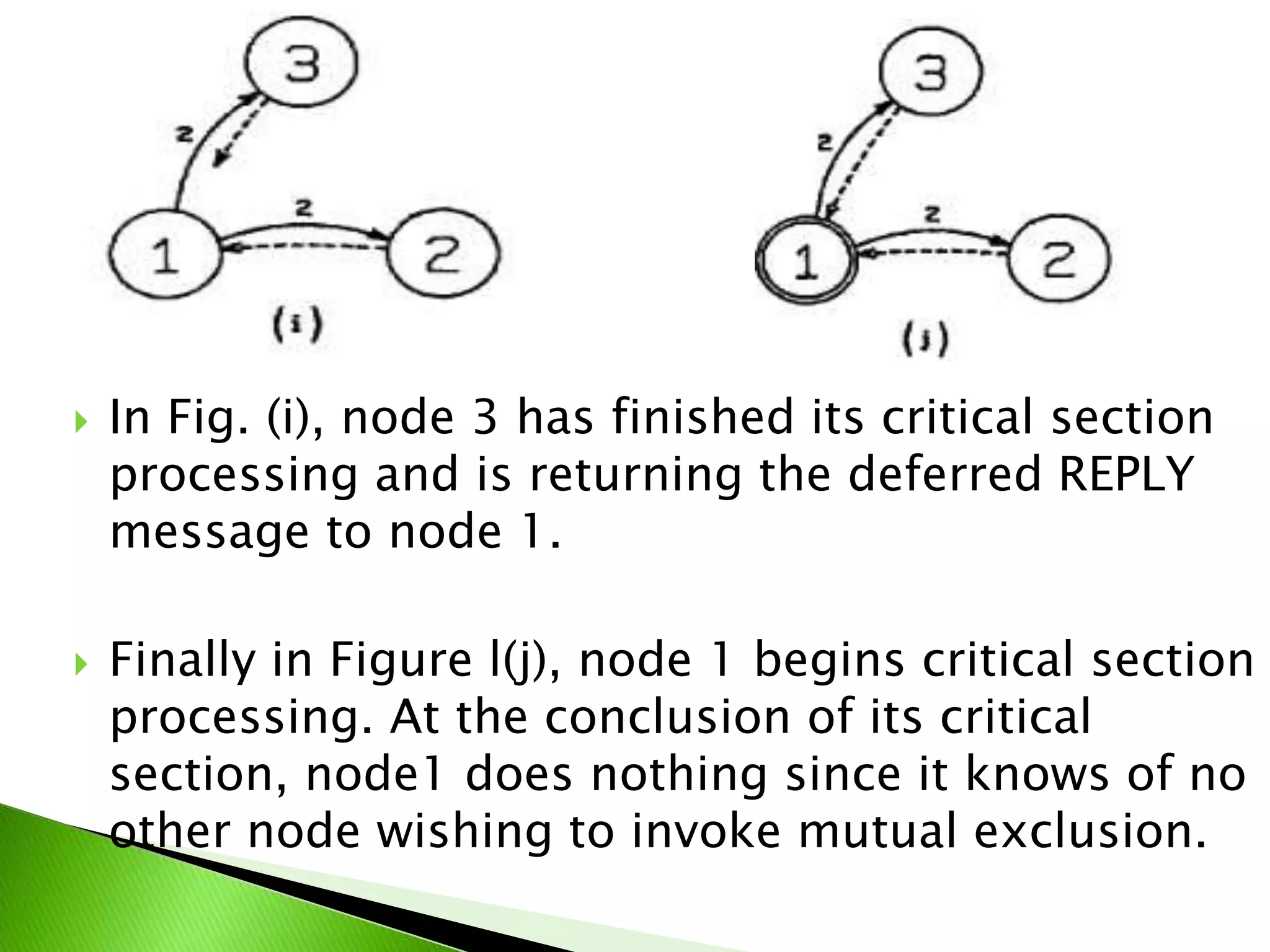
The document proposes an algorithm for achieving mutual exclusion between nodes with minimal messaging. It uses sequence numbers and node IDs to determine priority. Only 2(N-1) messages are required. The algorithm guarantees mutual exclusion, avoids deadlock and starvation, and has minimal delay. It is optimal in terms of message complexity.