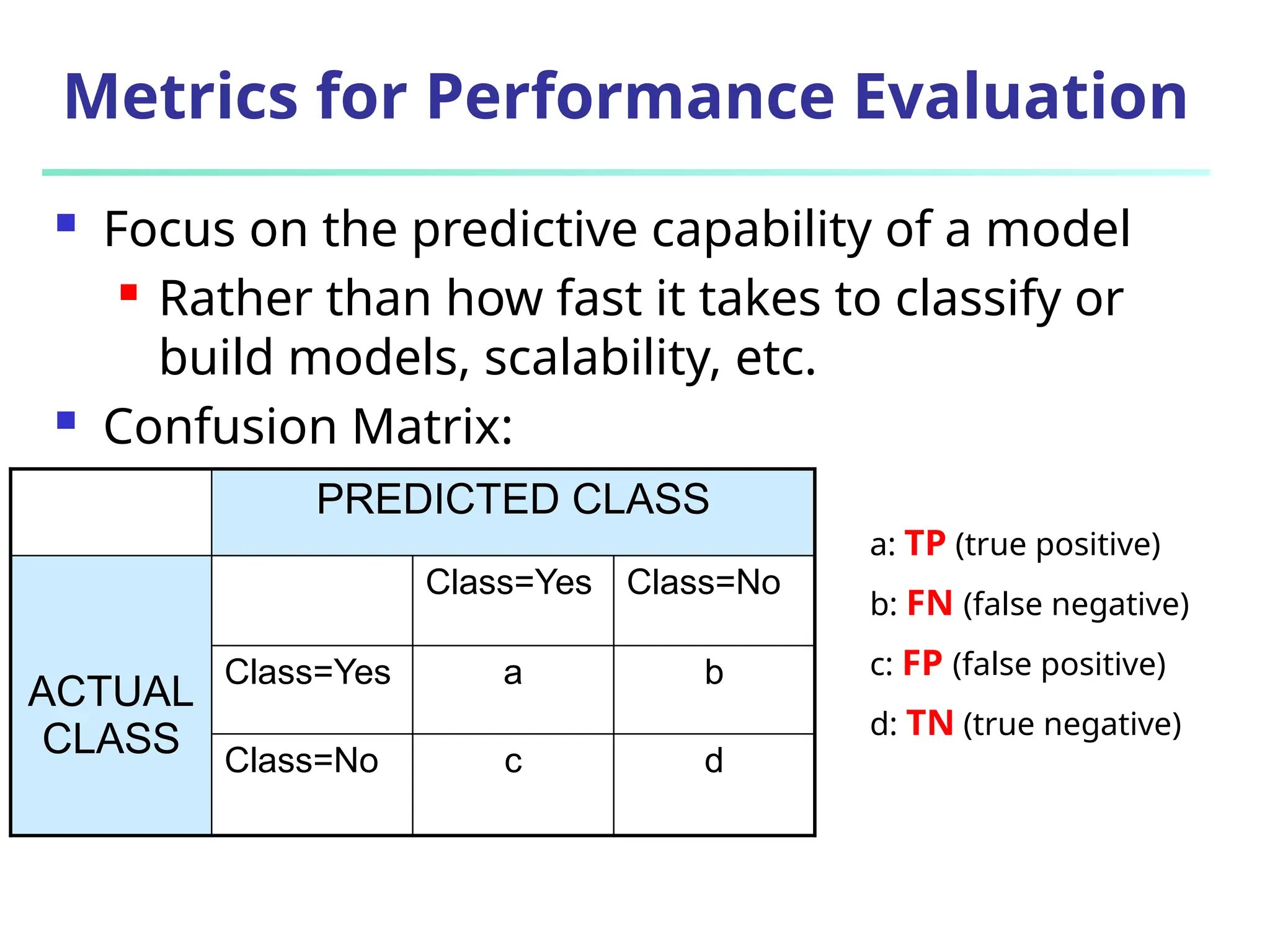
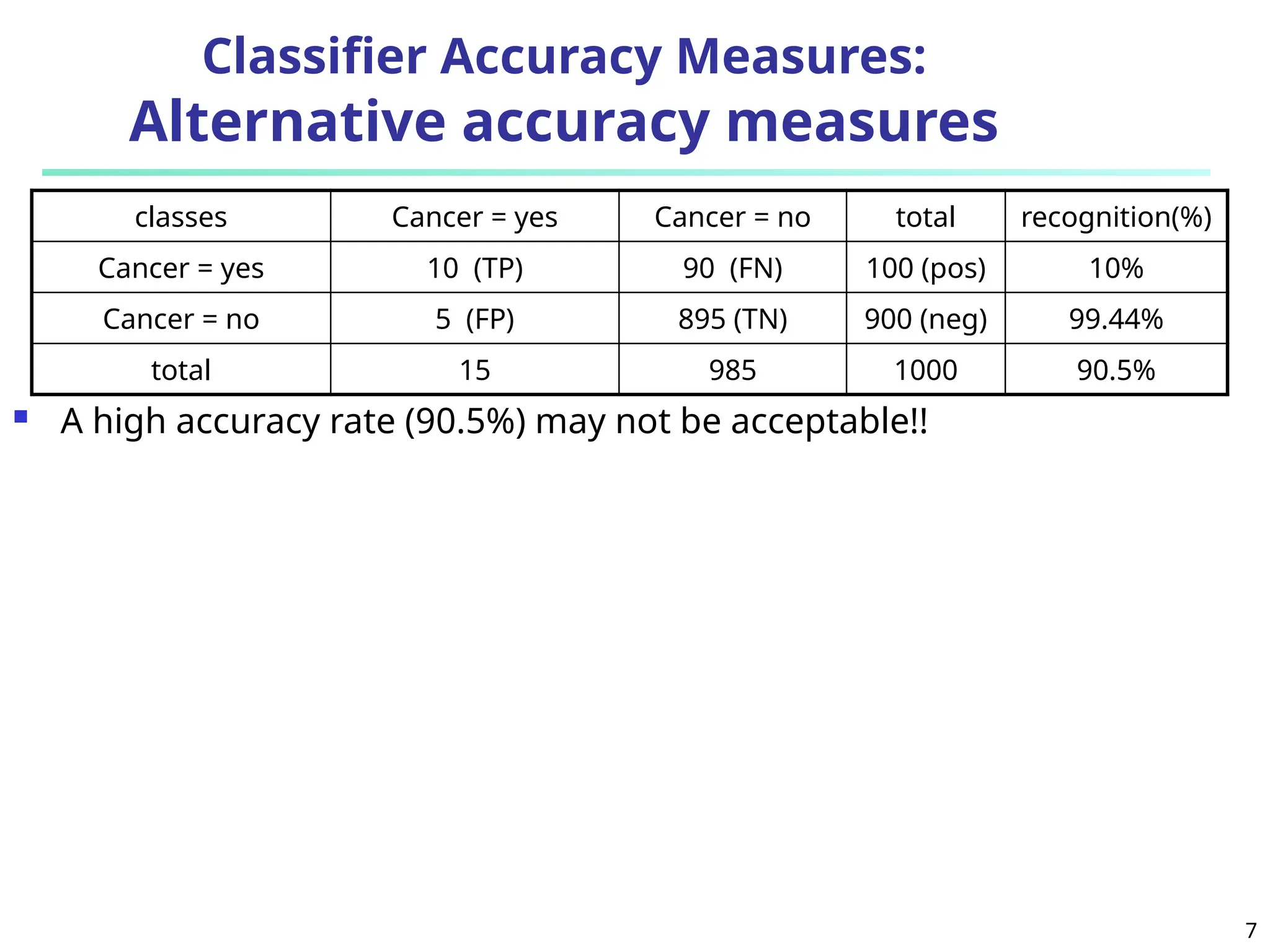
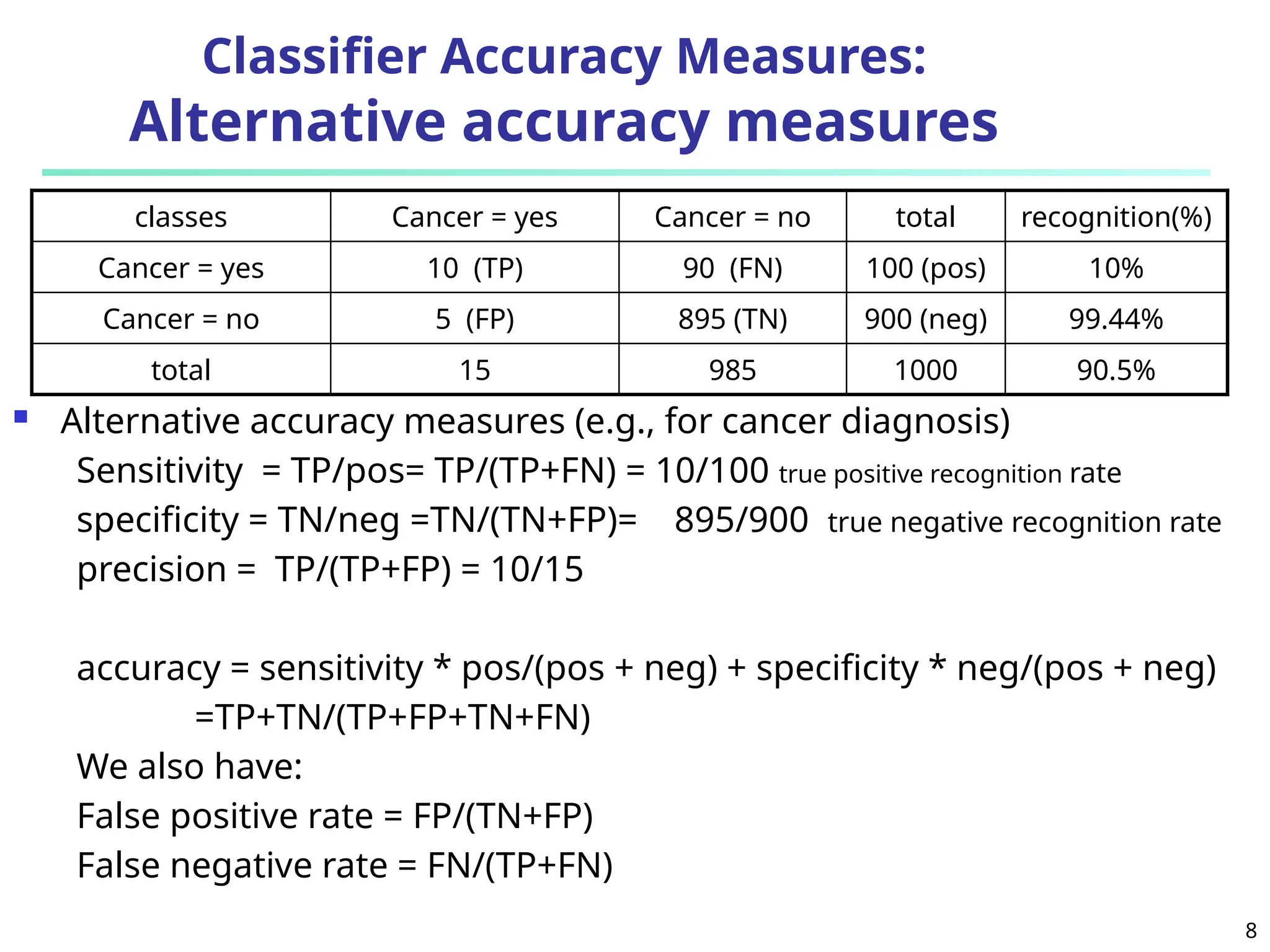
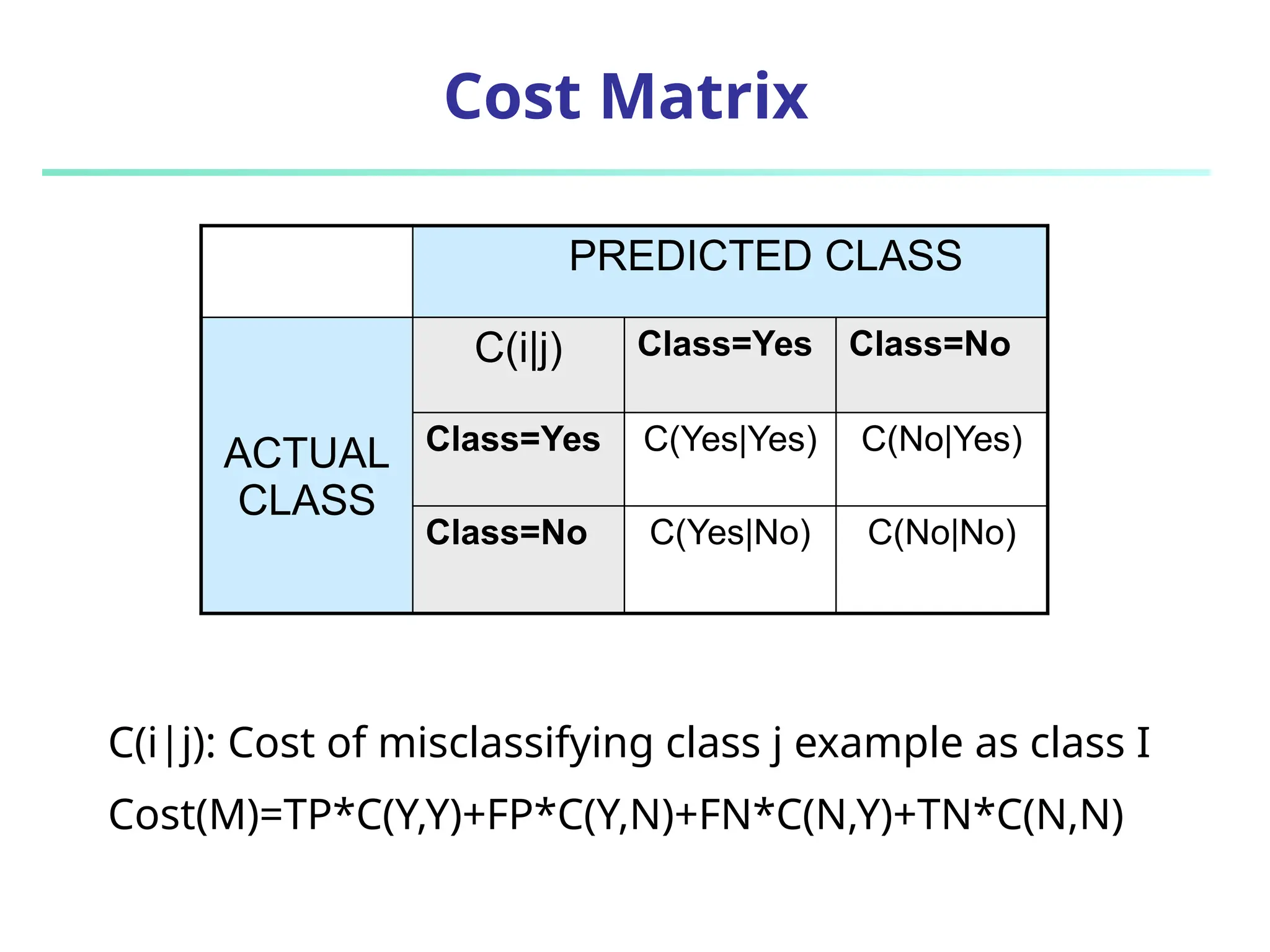
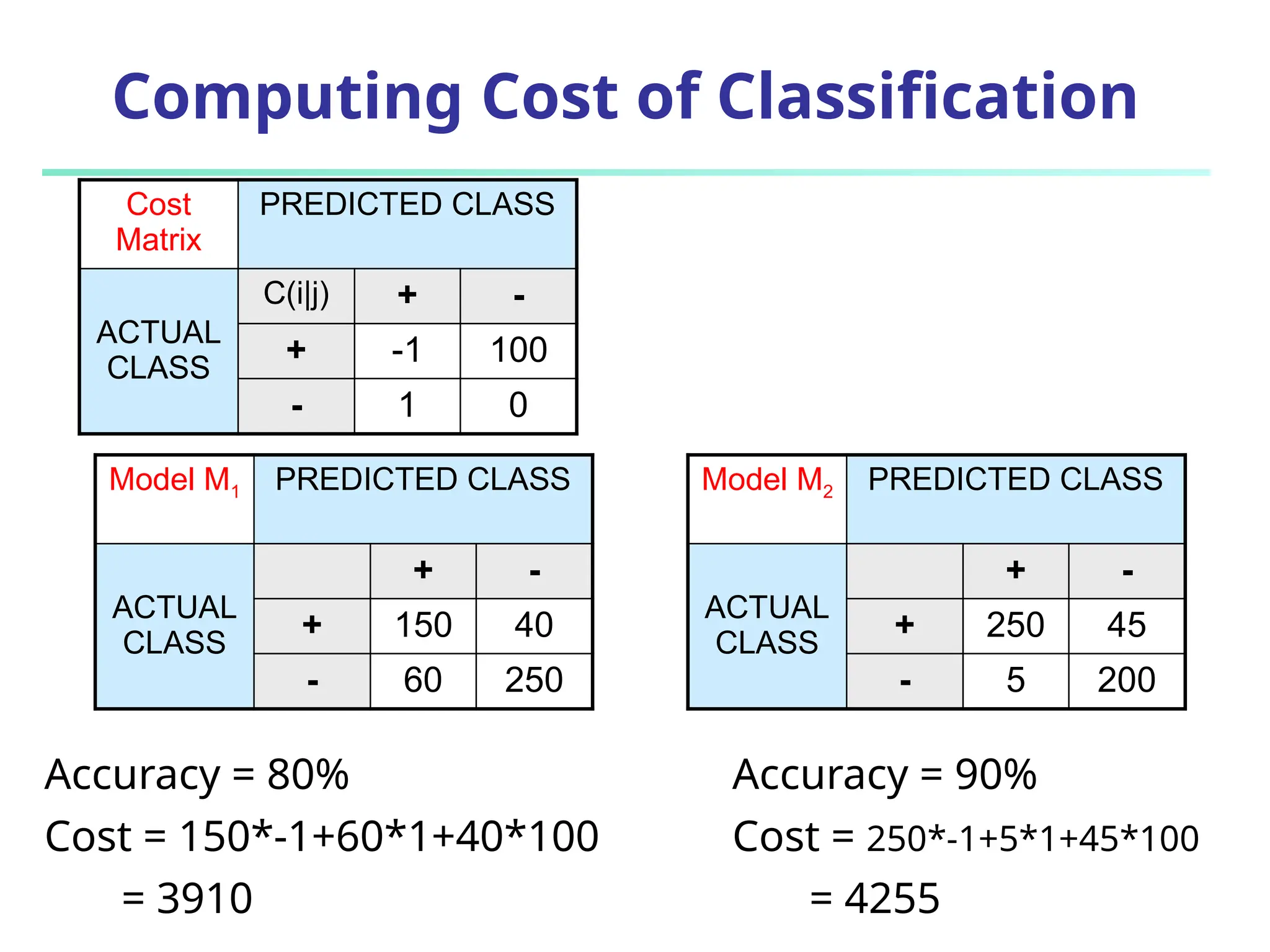
The document discusses model evaluation metrics for data mining classification, emphasizing performance evaluation techniques rather than model building speed. It explains various accuracy measures, such as sensitivity, specificity, precision, and the limitations of relying solely on accuracy. Additionally, the document outlines methods for obtaining reliable performance estimates, including holdout, cross-validation, and bootstrap sampling techniques.