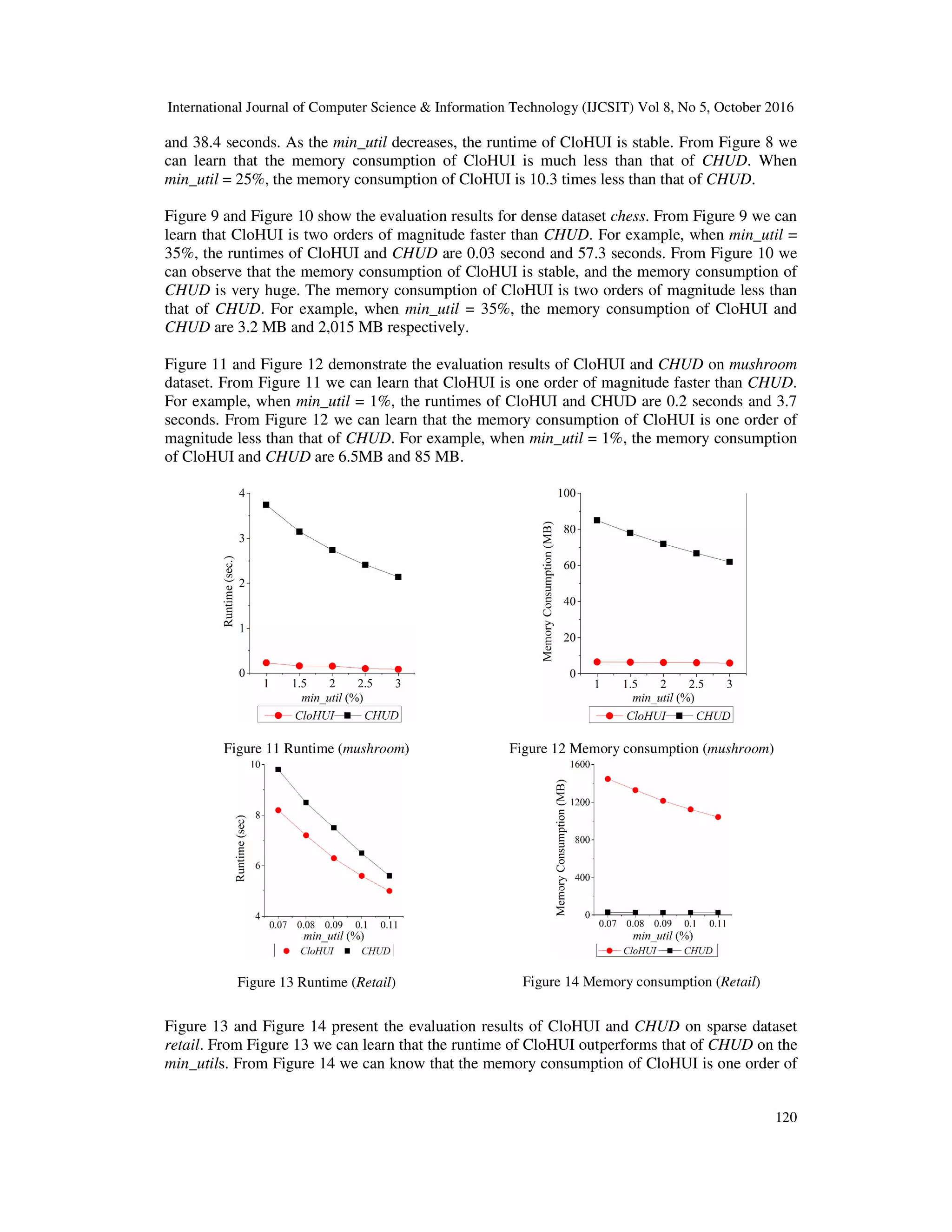
The document presents an efficient algorithm called Clohui for mining Closed + High Utility Itemsets (CHUIs) from transaction databases, addressing inefficiencies in existing High-Utility Itemset Mining (HUIM) methods. Clohui operates without generating candidate CHUIs by utilizing a tree structure for verification, significantly improving runtime and memory usage compared to the state-of-the-art algorithm CHUD. Experimental results demonstrate that Clohui is more than an order of magnitude faster and consumes less memory, especially for dense datasets.
![International Journal of Computer Science & Information Technology (IJCSIT) Vol 8, No 5, October 2016 DOI:10.5121/ijcsit.2016.8508 105 CLOHUI: AN EFFICIENT ALGORITHM FOR MINING CLOSED + HIGH UTILITY ITEMSETS FROM TRANSACTION DATABASES Shiming Guo and Hong Gao School of Computer Science, Harbin Institute of Technology, Harbin, China ABSTRACT High-utility itemset mining (HUIM) is an important research topic in data mining field and extensive algorithms have been proposed. However, existing methods for HUIM present too many high-utility itemsets (HUIs), which reduces not only efficiency but also effectiveness of mining since users have to sift through a large number of HUIs to find useful ones. Recently a new representation, closed+ high-utility itemset (CHUI), has been proposed. With this concept, the number of HUIs is reduced massively. Existing methods adopt two phases to discover CHUIs from a transaction database. In phase I, an itemset is first checked whether it is closed. If the itemset is closed, an overestimation technique is adopted to set an upper bound of the utility of this itemset in the database. The itemsets whose overestimated utilities are no less than a given threshold are selected as candidate CHUIs. In phase II, the candidate CHUIs generated from phase 1 are verified through computing their utilities in the database. However, there are two problems in these methods. 1) The number of candidate CHUIs is usually very huge and extensive memory is required. 2) The method computing closed itemsets is time consuming. Thus in this paper we propose an efficient algorithm CloHUI for mining CHUIs from a transaction database. CloHUI does not generate any candidate CHUIs during the mining process, and verifies closed itemsets from a tree structure. We propose a strategy to make the verifying process faster. Extensive experiments have been performed on sparse and dense datasets to compare CloHUI with the state-of-the-art algorithm CHUD, the experiment results show that for dense datasets our proposed algorithm CloHUI significantly outperforms CHUD: it is more than an order of magnitude faster, and consumes less memory. KEYWORDS Closed+ high-utility itemsets, pattern growth, utility mining 1. INTRODUCTION Along with the evolution of information technology and network infrastructure, an unprecedented amount of data are constantly being generated and collected, such as web click data, stock ticker data and sensor network data. Discovering useful patterns hidden in a database plays an essential role in several data mining tasks, such as frequent itemsets mining (FIM) and high-utility itemset mining (HUIM). FIM is a fundamental research topic, and has various application domains [1]. Given a transaction database, each transaction contains a set of items. FIM refers to discovering the complete set of itemsets from the database whose support (i.e. the number of transactions in the database that contain an itemset) is no less than a user-specified minimum support threshold. However there are two limitations in FIM. 1) The relative importance of items (i.e. weight) in the database is not considered, such as unit profit of products in market basket analysis; 2) The quantity of items in each transaction of the database is not considered. Therefore FIM cannot satisfy the requirement of users who desire to discover itemsets with high profits, since profit consists of two aspects, unit profit and purchased quantity [2]. In view of this, HUIM has been proposed as an important research topic [3]. Intuitively utility is a measure of how useful an](https://image.slidesharecdn.com/8516ijcsit08-161105043656/75/CLOHUI-AN-EFFICIENT-ALGORITHM-FOR-MINING-CLOSED-HIGH-UTILITY-ITEMSETS-FROM-TRANSACTION-DATABASES-1-2048.jpg)
![International Journal of Computer Science & Information Technology (IJCSIT) Vol 8, No 5, October 2016 106 itemset is. Utility of items in a database consists of two aspects: 1) the importance of different items, which is called external utility like unit profit; 2) the importance of items in each transaction of a database, which is called internal utility like purchased quantity. Let us consider an online sale database in Table 1 and unit profit of items in Table 2. In Table 1, each item in a transaction is associated with a quantity showing how many of this product was purchased. For instance in the first transaction T1 the purchased quantity of item B is 1. Utility of an item can be defined as the product of its external utility and its internal utility. Utility of an itemset can be defined as the sum of utilities of all the items it contains. For example, in the second transaction T2 the profit (utility) of item B is 2 × 2 = 4. The profit (utility) of itemset {BD} is 2 × 2 + 2 × 2 = 8. HUIM is to discover all the itemsets from a database whose utilities in the database are no less than a given minimum utility threshold. HUIM is a kind of constraint-based mining, in which users are allowed to specify their focus through constraints to capture certain itemsets from transaction databases [2]. This kind of constraint is called utility constraint. HUIM has wide applications such as website click stream analysis, online e-commerce management and mobile commerce environment planning [4][5]. Up to now, extensive algorithms have been proposed for HUIM [6][7][8]. However they present too many HUIs, which reduces not only efficiency but also effectiveness of mining since users have to sift through a large number of HUIs to find useful ones. To reduce the number of HUIs and present fewer but more important HUIs to users, closed+ high-utility itemset (CHUI) has been proposed [9], which incorporates the closure property of frequent itemsets into HUIM. With the concept of CHUI, HUI can be divided into two categories, CHUI and non-closed+ high-utility itemset. For each one in non-closed high-utility itemsets, there must be a corresponding closed itemset in CHUIs. Thus, the number of CHUIs is much smaller than that of HUIs. Existing methods adopt two phases to mine CHUIs from transaction databases. In phase I, each itemset is first verified whether it is closed. If the itemset is closed, an overestimation technique is adopted to set an upper bound of the utility of the itemset in the database. The itemsets whose overestimated utilities are no less than a user-specified minimum utility threshold are selected as candidate CHUIs. In phase II, the candidates generated from phase I are verified through computing their utilities in the database to identify CHUIs. However, there are two problems in existing methods: 1) the number of the candidates generated from phase I is usually huge, and extensive memory is required; 2) it is time-consuming to adopt these methods to compute closed itemsets. To deal with these problems, in this paper we propose an efficient algorithm for mining CHUIs from transaction databases. The contributions in this paper are as follows: 1) We propose a new data structure HUITWU-Tree (high utility itemsets tree which arranges items according to transaction weighted utility of single itemsets) to store the information of itemsets in a transaction database, and a utility database is adopted to store the utility of items in each transaction of the database. 2) We propose an effective algorithm CloHUI to discover the complete set of CHUIs from a transaction database. CloHUI adopts pattern-growth methodology to divide the search space into several subspaces. Each itemset in each subspace is first verified whether it is closed. If the itemset is closed, its utility in the database is calculated from utility databases directly, i.e., during the mining process there is no candidate generation. 3) Extensive experiments have been performed on real and synthetic datasets to compare the performance of CloHUI with the state-of-the-art algorithm CHUD. The experimental results show that for dense datasets CloHUI outperforms CHUD significantly in terms of runtime and memory consumption: it is an order of magnitude faster and consumes less memory.](https://image.slidesharecdn.com/8516ijcsit08-161105043656/75/CLOHUI-AN-EFFICIENT-ALGORITHM-FOR-MINING-CLOSED-HIGH-UTILITY-ITEMSETS-FROM-TRANSACTION-DATABASES-2-2048.jpg)

![International Journal of Computer Science & Information Technology (IJCSIT) Vol 8, No 5, October 2016 108 u(D, T1) + u(E, T1) = 13, and the utility of the database is TU(T1) + TU(T2) + TU(T3) + TU(T4) = 48. Definition 7 An itemset X is a closed itemset if there exists no itemset X′ such that 1) X′ is a proper superset of X and 2) every transaction containing X also contains X′. For example, in the database of Table 1, {AE} is a closed itemset, since there exists no superset of {AE} with the same support. Definition 8 (Closed high-utility itemset) An itemset X is called a closed high utility itemset (CHUI) if the two following conditions are satisfied: 1) X is closed and 2) X is a HUI. Problem statement. Given a transaction database TDB and a minimum utility threshold min_util, CHUI mining refers to discovering the complete set of closed itemsets whose utilities in TDB are no less than min_util. Without loss of generality, for min_util we use absolute utility value describing our proposed algorithm and the percent of database utility for experimental evaluation. In HUIM, utility of an itemset does not have the downward-closure property, i.e., utility of an itemset does not decrease monotonically when adding items to the itemset. In fact, utility of any superset of an itemset may be larger than, less than or equal to that of the itemset. A naive method for HUIM is to enumerate all itemsets from a database by the principle of exhaustion. However, this method suffers from the problem of a large search space. Hence, how to effectively prune the search space is a crucial challenge in HUIM. To deal with this problem, "Transaction-Weighted Utility" has been proposed [6]. With this concept, we can overestimate the utility of an itemset in a database to prune the search space. Definition 9 Transaction-Weighted Utility (TWU) of an itemset X in a transaction database TDB is the sum of utilities of the transactions in TDB that contain X, and denoted as TWU(X) = ∑ TU( )⊆ ⋀ ∈ . Clearly, TWU(X) ≥ u(X). In addition, TWU satisfies the downward closure property. That is, for all Y ⊆X, TWU(Y) ≥ TWU(X). Thus TWU of itemsets can be used to prune the search space. For example, in the database of Table 1, the TWU of items is shown in Table 3. Suppose min_util = 18, item F and its superset cannot be HUIs. Thus F can be pruned in the search space. 2.2. RELATED WORK FIM is a foundational research topic and quite a few algorithms have been proposed for FIM [1], such as Apriori [10] and FP-Growth [11]. However these algorithms are all based on the support/frequency framework, which makes the itemsets with frequencies lower than a given threshold but more important be filtered. Thus HUIM has been proposed as an important research topic. Existing methods for HUIM can be classified into three categories. The first category is candidate generation-and-test approaches, such as Two-Phase [6] and IIDS [12]. They discover the complete set of HUIs with two phases. In phase I, an overestimation technique is adopted to calculate an upper bound of the utility of each itemset in the database. The itemsets whose overestimated utilities are no less than a given threshold are selected as candidate HUIs. The search space is traversed by breadth first search, and candidate HUIs of length (k + 1) are iteratively generated from a set of candidate HUIs of length k (k ≥ 1). In phase II, the candidates generated from phase I are verified through scanning the database one more time. The second category is pattern-growth methods, such as IHUP [4] and UPGrowth [7]. They are also based on two-phase framework, and generally adopt tree structures to store the information of itemsets and their overestimated utilities in the database. In phase I, instead of generating level-wise candidate HUIs, they recursively partition the database into sub-databases according to the candidate 1-](https://image.slidesharecdn.com/8516ijcsit08-161105043656/75/CLOHUI-AN-EFFICIENT-ALGORITHM-FOR-MINING-CLOSED-HIGH-UTILITY-ITEMSETS-FROM-TRANSACTION-DATABASES-4-2048.jpg)
![International Journal of Computer Science & Information Technology (IJCSIT) Vol 8, No 5, October 2016 109 Table 3 TWU Of Items Item A B C D E F TWU 36 35 23 35 38 12 Table 4. Revised Database Trans ID Transactions T1 (E, 1) (A, 1) (B, 1) (D, 1) (C, 1) T2 (E, 1) (B, 2) (D, 2) T3 (A, 1) (B, 1) (D, 1) (C, 1) T4 (E, 1) (A, 2) itemsets found and search for local candidate items to assemble longer global candidate HUIs. In phase II, the candidates are verified. The third category is vertically formatting methods, such as HUI-Miner [8]. In these methods each itemset isassociated with a vertical data format, i.e., TID list showing the transactions containing the itemset. The utility of an itemset in the database is calculated through its vertical data format. The search space is represented as a set-enumeration tree, and the vertical data format of (k + 1)-itemsets is computed through the join operation on the vertical data format of two certain subsets (k ≥ 1). However, the methods in the above categories generally generate too many HUIs. Thus CHUI mining has been proposed to deal with this problem. To our best knowledge, CHUD is the state-of-the-art algorithm for mining CHUIs from transaction databases [9]. In CHUD each itemset is associated with a TID list. The TID list of single itemsets is computed through scanning the original database twice. The TID list of (k + 1)- itemsets is computed through intersecting the TID list of two certain subsets (k ≥ 1). CHUD discovers the complete set of CHUIs with two phases. In phase I, each itemset is first checked whether it is closed through intersecting its TID list with the TID list of some single itemsets. If an itemset is closed, an overestimation technique is adopted to set an upper bound of the utility of the itemset in the database. The itemsets whose overestimated utilities are no less than a user- specified minimum utility threshold are selected as candidate CHUIs. In phase II, the candidates generated from phase I are verified through computing their utilities in the database. However the number of candidates is usually very huge and extensive memory is required. Moreover it is time- consuming to perform the join operation on the TID lists to identify a closed itemset. 3. PROPOSED DATA STRUCTURE In this section we proposed a novel data structure HUITWU-Tree to store the information of itemsets in a database, and a utility database is adopted to store the utility of items in each transaction of the database. Utility database is a two-dimension array. The length of utility database is the size of the longest transaction in the database, and the width of utility database is the number of transactions in the database. 3.1. HUITWU-TREE AND UTILITY DATABASE As stated in [4], item-arranging order in a tree structure can facilitate to improve the performance of algorithms. Support descending order, lexicographic order and TWU descending order are common used in algorithms. The experimental results in [4] show the algorithm based on the tree structure where items are arranged in TWU descending order has the best execution time. Thus in our proposed tree structure TWU descending order is adopted. An initial HUITWU-Tree and a utility database can be constructed by two scans of a database. We call the HUITWU-Tree and the utility database generated from the database global HUITWU-Tree and global utility database. Firstly, the TWU of all the items in the database is accumulated by a database scan. If TWU of an item is less than a given minimum utility threshold, the item and its](https://image.slidesharecdn.com/8516ijcsit08-161105043656/75/CLOHUI-AN-EFFICIENT-ALGORITHM-FOR-MINING-CLOSED-HIGH-UTILITY-ITEMSETS-FROM-TRANSACTION-DATABASES-5-2048.jpg)
![International Journal of Computer Science & Information Technology (IJCSIT) Vol 8, No 5, October 2016 110 supersets cannot be HUIs, which means they also cannot be CHUIs. The items whose TWUs are no less than the threshold are collected into a set named SET. The remaining items are sorted according to TWU descending order, and the item order is denoted as R. Secondly, the database is scanned for the second time. In each transaction of the database, the items appearing in SET are removed, and then the remaining items are sorted according to R. The new transaction is called revised transaction. For example, in the database of Table 1, suppose the minimum utility threshold min_util = 18, the TWU of items after the first database scan is shown in Table 3. From Table 3 we can learn that item F can be removed from the database, and the item order is (E, A, B, D, C). After the second scan of the database all the transactions are revised. The database after revising is called revised database, and the revised database of Table 1 is shown in Table 4. As stated in [5], the tree-based framework for HUIM applies the divide-and-conquer technique in the mining process. Let (i1, i2, …, in) be the items in the header table of tree structures. The search space is divided into the following subspaces: • {in}’s conditional tree (abbreviated as {in}-Tree); • {in−1}-Tree without containing item in; • ···; • {ij}-Tree without containing any item in {ij+1, ..., in}; and so on until j = 1. It can be observed that in the subspace {ij}-Tree (1 ≤ j < n), all paths are not related to any item in {ij+1, ..., in}, i.e., the items that are descendant nodes of item ij in a global tree will not appear in {ij}-Tree. From this viewpoint, prefix utility of an item in a transaction is proposed to facilitate estimating the true utility of an itemset [13]. Definition 10 Assume the items in Td are listed in transaction-weighted utility descending order. The prefix set of ip in Td consists of all the items in Td that are not listed after ip, which is denoted as PrefixSet(ip, Td). Definition 11 Prefix utility of an item ip in a transacrion Td is the sum of the utilities of the items of PrefixSet(ip, Td) in Td, and defined as PrefixUtil(ip, Td) = ∑ ( , )∈ ( , ) . Definition 12 Prefix utility of an item ip in a database TDB is the sum of the prefix utilities of ip in all the transactions of TDB that contain ip, and defined as ∑ Pre ixUtil( , )∈ ∧ ∈ . For example, in Table 4, PrefixSet(B, T1) is {ABE}. The prefix utility of item B in T1 is PrefixUtil(B, T1) = u(E, T1) + u(A, T1) + u(B, T1) = 3 + 5 + 2 = 10. The prefix utility of item B in the database is PrefixUtil(B, T1) + PrefixUtil(B, T2) + PrefixUtil(B, T3) = 24. With the concept of prefix utility of an item in a database, HUITWU-Tree is defined as follows: Definition 13 (HUITWU-Tree) A HUITWU-Tree is a tree structure satisfying the following conditions: 1) It consists of one root labeled as null, a set of item prefix subtrees as the children of root and a header table. 2) Each node in an item prefix subtree consists of four fields: item_name, support, node_link and tp_link. Item_name records which item this node represents. Support registers the number of the transactions falling onto the path from the root to the node. Node_link links to the next node in a HUITWU-Tree carrying the same item_name. Tp_link is an array whose elements are the links to the transactions in a utility database.](https://image.slidesharecdn.com/8516ijcsit08-161105043656/75/CLOHUI-AN-EFFICIENT-ALGORITHM-FOR-MINING-CLOSED-HIGH-UTILITY-ITEMSETS-FROM-TRANSACTION-DATABASES-6-2048.jpg)
![International Journal of Computer Science & Information Technology (IJCSIT) Vol 8, No 5, October 2016 111 3) Each entry in the header table consists of three fields, (1) item_name, (2) prefix utility of an item in a database and (3) head of node_link, which points to the first node in a HUITWU-Tree carrying the same item_name. The construction of an initial global HUITWU-Tree and a global utility database is presented in Algorithm 1. Figure 1. Global HUITWU-Tree and global utility database An example is given to explain how to construct an initial global HUITWU-Tree and a global utility database. In the database of Table 4, the revised transactions are inserted into the global HUITWU-Tree as follows. When T1 = {(E, 1) (A, 1) (B, 1) (D, 1) (C, 1)} is retrieved, the first node NE (The item_name of this node is E) is created (line 9 - 10). The utility of item E in T1 is 3 × 1 = 3, which is stored in the first record of utility database (line 12 - 13). The prefix utility of E in T1 is calculated, and accumulated into the prefix utility of E in the header table (line 14 - 16). The same operation is conducted on item A, B, D and C. Since C is the last item of T1, the transaction identification T1 is inserted into NC.tp_link (line 17 - 18). After inserting all the transactions in the revised database of Table 4, the global HUITWU-Tree and the global utility database are constructed, which are shown in Figure 1. Note in Figure 1 we present items in each record of the utility database just for describing the relations between items and their utilities in the transactions. In fact in our implementation we just store the utility of items in the transactions instead of items and their utilities in the transactions to reduce memory consumption. Thus the items in the utility database of Figure 1 are presented with 50% transparency. 3.2. COMPUTING CLOSURES As stated in [9], different join orders between utility constraint and closed constraint produce the same result sets. In CloHUI closed itemsets are computed first, and then the complete set of CHUIs is discovered from the result set. The divide-and-conquer framework for mining closed itemsets in [14] is adopted in CloHUI. Similar to FP-Growth [11], suppose the items in the header table are (i1, i2, …, in), the problem of mining the complete set of closed itemsets can be divided into n sub-problems: The jth problem (1 ≤ j ≤ n) is to find the complete set of closed itemsets containing in+1-j but no ik (for n + 1 - j < k ≤ n). We refer readers to [14] for more details about the related techniques. As stated in [14], each closed itemset generated from FP-Tree needs to be checked whether it is subsumed by some already found closed itemset with identical support.](https://image.slidesharecdn.com/8516ijcsit08-161105043656/75/CLOHUI-AN-EFFICIENT-ALGORITHM-FOR-MINING-CLOSED-HIGH-UTILITY-ITEMSETS-FROM-TRANSACTION-DATABASES-7-2048.jpg)
![International Journal of Computer Science & Information Technology (IJCSIT) Vol 8, No 5, October 2016 112 Algorithrim 1 (Construction of global HUITWU-Tree and global utility database) Input: The revised database TDB Output: A global HUITWU-Tree Tree and a global utility database UDB 01: Create the root R of Tree, and label it as null 02: Initialize the header table Header of Tree with the items in TDB 03: Set the prefix utilities of all the items in Header as 0 04: For each transaction Trans in TDB 05: Allocate a record Record from UDB for Trans 06: Call Insert_trans(Trans, R, Record, Header) Insert_trans(Trans, R, Record, Header) 07: Let Trans be represented as [p|P], where p is the first element and P is the remaining list 08: If R does not have a child N with N.item_name = p.item_name, then 09: Create a new node N as a child of R 10: N.item_name = p.item_name 11: Let N.node_link be linked to the nodes with the same item_name 12: Calculate p.utility in the transaction Trans 13: Store p.utility in Record 14: Calculate p.prefix_utility 15: Find the entry E in Header with p.item_name 16: Increase E.prefix_utility by p.prefix_utility 17: If P is empty, then 18: Insert the TID of Trans into N.tp_link 19: Else 20: Call Insert_trans(P, N, Record, Header) When the number of close itemsets is very huge, this operation is costly. In [15], a new theoretical framework has been proposed to avoid comparing a candidate closed itemset with already found closed itemsets. In this framework, each itemset is associated with a TID list and the search space is a set-enumeration tree. If the TID list of an itemset is a subset of that of some single itemsets, the itemset is not closed. For example, given a total order relation R defined among item literals, for an item ip if there exists an item iq which appears before ip according to R such that the TID list of ip is a subset of that of iq, {ip} is not a closed itemset. According to the theory in [15], we propose a novel optimization strategy to verify closed itemsets in a tree structure. Definition 14 For a non-root node N of HUITWU-Tree whose item_name is ip, the subtree rooted at N is denoted as subT. If there exists an item iq such that the support of iq in subT is the same as the support of the node N in the HUITWU-Tree, N is called a non-closed node and iq is called a closed item of N; otherwise, N is called a closed node. For example, in the global HUITWU-Tree of Figure 1 there are three nodes whose item_name is B. For each node NB the support of item D in the subtree rooted at NB is the same as the support of the node NB in the HUITWU-Tree, which is 1. Thus the three nodes are non-closed nodes and item D is a closed item of the three nodes. Lemma 1 For each item ip in the header table, if the tree nodes obtained from traversing the node link started from the entry in the header table are all non-closed nodes and there exists an item iq which is a closed item of the above non-closed nodes, the itemsets where ip is the last item are not closed itemsets. Proof. Since iq is a closed item of each non-closed node, the projected paths of {ipiq} are the same as the projected paths of {ip}. For example, in the global HUITWU-Tree of Figure 1, the projected paths of {BD} are A, E and E → A, which are the same as the projected paths of {B}. Each itemset X generated from ip-conditional pattern tree must have the same support with X ∪ iq. Thus X is not a closed itemset.](https://image.slidesharecdn.com/8516ijcsit08-161105043656/75/CLOHUI-AN-EFFICIENT-ALGORITHM-FOR-MINING-CLOSED-HIGH-UTILITY-ITEMSETS-FROM-TRANSACTION-DATABASES-8-2048.jpg)
![International Journal of Computer Science & Information Technology (IJCSIT) Vol 8, No 5, October 2016 113 (a) (b) (c) (d) Figure 2. Transfer process of arrays in the global HUITWU-Tree (a) C → D (b) D → B (c) B → A (d) A → E In a global HUITWU-Tree we maintain an array for each leaf node to record the support of descendent nodes. The length of the array is the number of items in the header table. For example, in the global HUITWU-Tree of Figure 1 there exists three arrays and the length of each array is 5. In CloHUI the header table are traversed from bottom to up to compute closed itemsets from a HUITWU-Tree. For each item ip in the header table there are three phases to compute the closed itemsets where ip is the last item. In phase I, ip is checked whether it can be pruned according to lemma 1, i.e., whether the conditions in lemma 1 are satisfied by the nodes whose item_names are ip. If ip cannot be pruned, ip-conditional database is generated and i-conditional pattern tree is constructed in phase II. Then closed itemsets are mined from i-conditional pattern tree. In phase III, when the closed itemsets containing ip have been finished, the arrays associated with the nodes whose item_names are ip are transferred to their parents in the HUITWU-Tree for computing the closed itemsets where the remaining items in the header table are the last items. During the construction of conditional pattern tree in phase II, if there are items appearing in each transaction of conditional database, the item-merging strategy is adopted [14]. Lemma 2 (Item-merging strategy) If a local item ip appears in each transaction of X’s conditional database, the conditional itemset can be adjusted to X ∪ {ip} and there is no closed itemset missing. (We refer readers to [14] for the proof). Let’s use the global HUITWU-Tree in Figure 1 to examine how to compute closed itemsets. For the global HUITWU-Tree, the transfer process of the arrays associated with leaf nodes is shown in Figure 2. When the arrays associated with the tree nodes are transferred, the support in these tree nodes is accumulated into the arrays. For example in Figure 2(a) the support in the nodes Figure 3. {BD}’s conditional pattern tree Figure 4. Transfer process from A to E](https://image.slidesharecdn.com/8516ijcsit08-161105043656/75/CLOHUI-AN-EFFICIENT-ALGORITHM-FOR-MINING-CLOSED-HIGH-UTILITY-ITEMSETS-FROM-TRANSACTION-DATABASES-9-2048.jpg)

![International Journal of Computer Science & Information Technology (IJCSIT) Vol 8, No 5, October 2016 115 4. PROPOSED ALGORITHM In this section we propose an efficient algorithm named CloHUI for mining CHUIs from transaction databases. Similar to UP-Growth [7], CloHUI adopts pattern-growth methodology and the bottom-up order is used to traverse the header table of HUITWU-Tree. As stated in [13], prefix utility of an item in a database has the downward closure property, and lemma 3 is proposed in [13]. Lemma 3 Assume that items in all the transactions of a database TDB are listed in TWU descending order. Let X be an nonempty itemset where ip is the last item of X, PrefixUtil(ip, TDB) ≥ u(X) (We refer readers to [13] for the proof). This lemma means that for a global HUITWU-Tree, if prefix utility of an item ip in a database is less than min_util, the itemsets where ip is the last item according to item order R cannot be HUIs (They also cannot be CHUIs), i.e., there is no need to construct {ip}-Tree. Thus the prefix utility of items in the header table can be used to prune the search space. If the prefix utility of item ip in the header table is no less than min_util, there are four steps in CloHUI to compute the CHUIs where ip is the last item according to item order R. 1) The conditions in lemma 1 are checked. If the conditions are satisfied, Step 2 and 3 are skipped; 2) {ip}’s conditional database is generated by tracing the paths in the global tree, and a conditional pattern tree is constructed by the information in {ip}’s conditional database; 3) CHUIs are iteratively mined from the conditional pattern tree; 4) the information related to ip in the global HUITWU-Tree and the global utility database is updated. If the prefix utility of item ip in the header table is less than min_util, only Step 4 is performed. Generating a conditional database. For an item ip in the header table of a global HUITWU-Tree (1 ≤ p ≤ n), if the prefix utility of ip in the header table is no less than min_util, {ip}’s conditional database is generated as follows. First, the node links in the global tree corresponding to ip are traced. Found nodes are traced to the root of global tree, and all the paths related to ip can be retrieved and collected into {ip}’s conditional database. Moreover the utility of items in the paths can also be collected into {ip}’s conditional database from the global utility database with the tp_link of found nodes. Table 5. {D}’s conditional database TID Transactions Merging item Condition T1 (E, 1) (A, 1) (B, 1) (D, 1) T2 (E, 1) (B, 2) (D, 2) T3 (A, 1) (B, 1) (D, 1) Figure 5 {BD}’s conditional pattern tree and conditional utility database Example 1. In the global HUITWU-Tree and the global utility database of Figure 1, item C in the header table is considered first. Suppose min_util = 18, since the prefix utility of C in the header table is greater than min_util, {C}’s conditional database is generated. The link queue started](https://image.slidesharecdn.com/8516ijcsit08-161105043656/75/CLOHUI-AN-EFFICIENT-ALGORITHM-FOR-MINING-CLOSED-HIGH-UTILITY-ITEMSETS-FROM-TRANSACTION-DATABASES-11-2048.jpg)
![International Journal of Computer Science & Information Technology (IJCSIT) Vol 8, No 5, October 2016 116 from the head of node_link in the entry of C is traced. Two paths E → A → B → D → C and A → B → D → C are retrieved. {C}’s conditional database is {[(A, 1) (B, 1) (C, 1) (D, 1) (E, 1)], [(A, 1) (B, 1) (C, 1) (D, 1)]}. Since item A, B and D appear in each transaction of {C}’s conditional database, item merging strategy is adopted and the conditional itemset is adjusted to {ABCD}. The first closed itemset {ABCD} is obtained and the utility of {ABCD} in the database is calculated, which is 20. Then we can learn that {ABCD} is a CHUI. Constructing a conditional HUITWU-Tree. A conditional HUITWU-Tree can be constructed by two scans of a conditional database. For {ip}’s conditional database, the TWU of items in the conditional database is calculated during the first scan. The items whose TWUs are less than min_util and the ones appearing in each transaction of {ip}’s conditional database are collected into a set which is denoted as S. The remaining items are sorted according to TWU descending order, and the item order is denoted as R′. During the second scan of the conditional database, the items in S are removed from the transactions. The remaining items are sorted according to R′. The revised transactions in the {ip}’s conditional database are inserted into a conditional HUITWU-Tree which has the similar structure with a global HUITWU-Tree except that 1) the root of conditional HUITWU-Tree is labelled as the conditional itemset, and 2) for an item iq in the header table, the utilities of the condition itemset in all the transactions where the condition itemset and iq co-exist need to be accumulated into the prefix utility of iq in the header table. Example 2. In the global HUITWU-Tree of Figure 1, {D}’s conditional database is shown in Table 5. Since item B appears in each transaction of {D}’s conditional database, item-merging strategy is adopted and the conditional itemset is adjusted to {BD}. The TWU of items in {BD}’s conditional database is calculated during the first scan and the results are {(E: 24), (A: 23)}. The number beside each item is its TWU. The root of {BD}’s conditional HUITWU-Tree is created, and is labeled as {BD}. The header table is initialized with the items whose TWUs are no less than min_util according to TWU descending order. During the second scan, the first revised transaction {E, A} in Table 5 forms the first branch adhered to the root of {BD}’s conditional HUITWU-Tree. The tp_link of the node NA which corresponds to the last item of {E, A} is set to T1. The utilities of item E and A in T1 are stored in the first record of {BD}’s conditional utility database. The sum of the prefix utility of E in T1 and the utility of the condition itemset {BD} in T1 is 3 + 4 = 7, which is accumulated into the prefix utility of E in the header table. The same calculation is conducted for item A. The second revised transaction and the third one are dealt with in the same way. The {BD}’s conditional HUITWU-Tree and the {BD}’s conditional utility database are shown in Figure 5. Mining CHUIs from a conditional HUITWU-Tree. Mining CHUIs from a conditional HUITWU- Tree has the same steps as a global HUITWU-Tree. The header table is traversed in bottom-up order. For each item iq in the header table, if the prefix utility of iq in the header table is no less than min_util, the conditions in lemma 1 are checked in Step 1. If the conditions are satisfied, (a) (b)](https://image.slidesharecdn.com/8516ijcsit08-161105043656/75/CLOHUI-AN-EFFICIENT-ALGORITHM-FOR-MINING-CLOSED-HIGH-UTILITY-ITEMSETS-FROM-TRANSACTION-DATABASES-12-2048.jpg)

![International Journal of Computer Science & Information Technology (IJCSIT) Vol 8, No 5, October 2016 118 10: Results ← Results ∪ Y 11: Construct Y’s conditional HUITWU-Tree Tree′ and Y’s utility database UDB′ 12: If Tree′ is not empty then 13: call CloHUI(Tree′, UDB′, min_util, Y, Results) 14: Update the information of Tree and UDB related to ip 15: Transfer the arrays associated with the nodes Nip to their parents 16: Return Results In summary, for the dataset in Table 1, suppose min_util = 18, the CHUIs in the order of output are {{ABCD}: 20, {BDE}: 18, {A}: 20, {AE}: 21}. The number after “:” is the utility of itemsets in the database. Based on above analysis, the pseudo code of CloHUI is in Algorithm 2. If the input parameter Tree is a global HUITWU-Tree, the condition itemset X is empty. At first Results used to store CHUIs from a database is initially set to null. The complete set of CHUIs is generated by recursively calling the procedure CloHUI(global HUITWU-Tree, global utility database, min_util, ϕ, Results). The header table is traversed in bottom-up order (line 1). If the prefix utility of item ip in the header table is no less than min_util (line 2), the conditions in lemma 1 are checked (line 3). If the conditions in lemma 1 are not satisfied, the conditional database of itemset Y = X ∪{ip} is generated (line 5). The items appearing in each transaction of conditional database are merged into the conditional itemset (line 6 - 7) and the utility of conditional itemset is calculated (line 8). If it is a HUI, we can learn it is a CHUI (line 9 - 10). Then a conditional HUITWU-Tree and a utility database of the condition are constructed (line 11). If the conditional HUITWU-Tree is not empty, CloHUI(conditional HUITWU-Tree, conditional utility database, min_util, Y, Results) is called (line 12 - 13). After the itemsets where ip is the last item have been computed, the information related to ip is updated in X’s HUITWU-Tree and X’s utility database (line 14 - 15). 5. EXPERIMENTAL EVALUATION In this section, the performance of CloHUI is evaluated and compared with the state-of-the-art algorithm CHUD. We take runtime and peak memory consumption as the evaluation criteria, which are adopted in [8]. Running time contains input time, CPU time and output time. When measuring running time, we varied min_utils for each dataset. Since CloHUI does not generate any candidate, we also report the number of candidates in CHUD. Experiments are performed on a computer with 2.93 GHz Intel Core 2 Processor and 4 GB memory. The operating system is Ubuntu 12.04. All the algorithms are implemented in C++. The “time” command is adopted to measure the runtime of algorithms and the “massif” tool in the software “valgrind”1 is used to record the memory consumption of algorithms Table 6. Datasets′ characteristics Database No. of Trans No. of Items AvgLen MaxLen Type Mushroom 8,124 119 23 23 Dense Chess 3,196 75 37 37 Dense Accidents 340,183 468 33.8 51 Dense Retail 88,162 16,470 10.3 76 Sparse T40I10D100K 100,000 942 39.6 77 Dense T10I4D100K 100,000 870 10.1 29 Sparse 1 Valgrind: A GPL’d System for Debugging and Profilling Linux Program. http://valgrind.org.](https://image.slidesharecdn.com/8516ijcsit08-161105043656/75/CLOHUI-AN-EFFICIENT-ALGORITHM-FOR-MINING-CLOSED-HIGH-UTILITY-ITEMSETS-FROM-TRANSACTION-DATABASES-14-2048.jpg)
![International Journal of Computer Science & Information Technology (IJCSIT) Vol 8, No 5, October 2016 119 Six datasets are used in our experiments, which were obtained from FIMI Repository2 . Datasets mushroom, chess, accidents and retail are real. Datasets T10I4D100K and T40I4D100K are synthetic, and were generated by IBM Quest Synthetic Data Generation Code. “T” means average transaction length, “I” represents average frequent itemset length and “D” refers to the number of transactions in a dataset. In above datasets, unit profit of items and purchased quantity of items in each transaction are not provided. Like the performance evaluation of the previous algorithms [6][7][8], unit profit of items is generated between 0.01 and 10 by using a lognormal distribution and quantity of items in each transaction is generated randomly between 1 and 10. Table 6 shows the characteristics of datasets used in the experiments, including the number of transactions, the number of distinct items, the average number of items in a transaction and the maximal number of items in the longest transaction. 5.1 EXPERIMENTS ON REAL-LIFE DATASET WITH SYNTHETIC UTILITY VALUES The performance evaluation of CloHUI and CHUD on accidents dataset are depicted in Figure 7 and Figure 8. From Figure 7 we can learn that CloHUI is an order of magnitude faster than CHUD. For example, when min_util = 25%, the runtimes of CloHUI and CHUD are 2 seconds Figure 7 Runtime (accidents) Figure 8 Memory consumption (accidents) Figure 9 Runtime (Chess) Figure 10 Memory Consumption (Chess) 2 http:// fimi.ua.ac.be/](https://image.slidesharecdn.com/8516ijcsit08-161105043656/75/CLOHUI-AN-EFFICIENT-ALGORITHM-FOR-MINING-CLOSED-HIGH-UTILITY-ITEMSETS-FROM-TRANSACTION-DATABASES-15-2048.jpg)
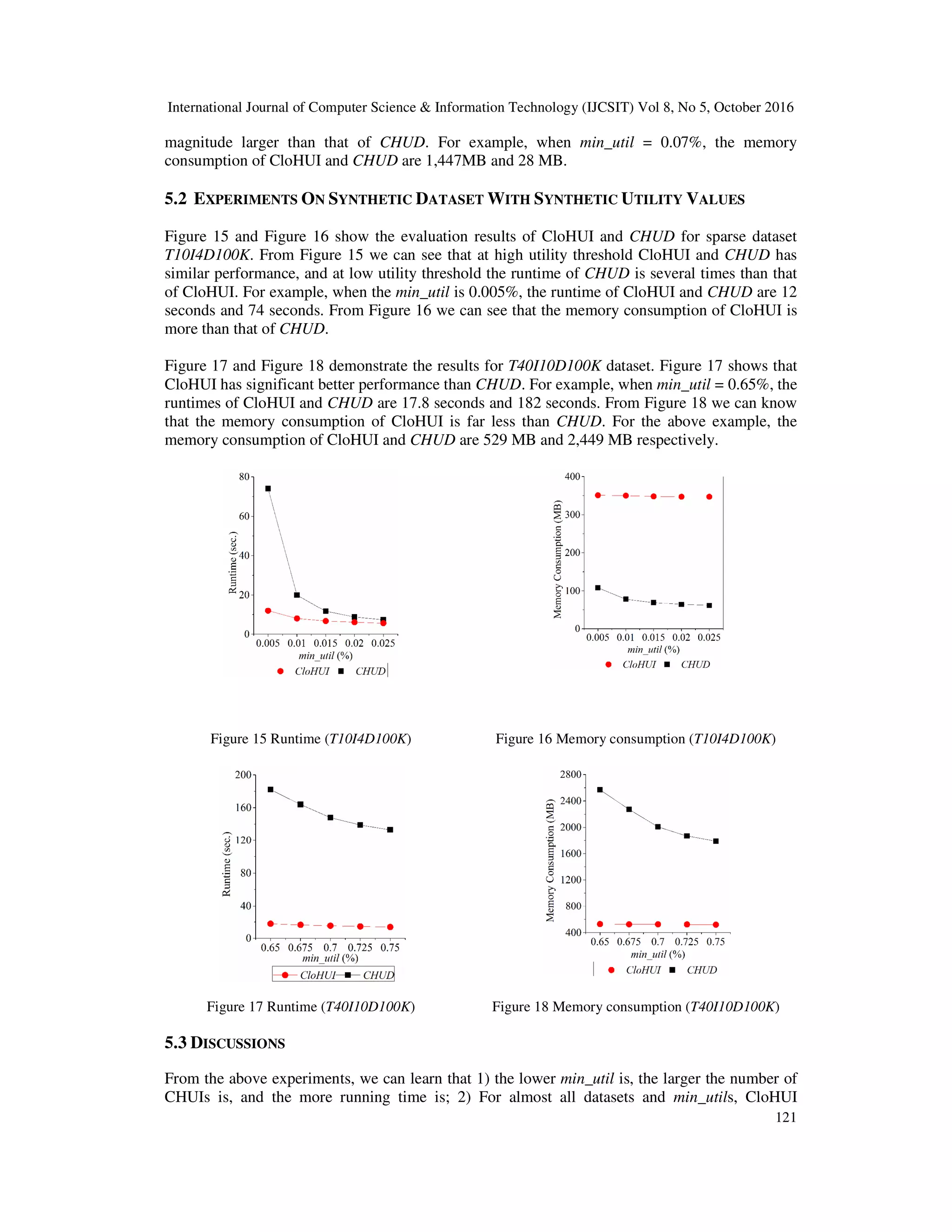

![International Journal of Computer Science & Information Technology (IJCSIT) Vol 8, No 5, October 2016 123 At last, compared to CLOSET [14], the optimization strategy we proposed can efficiently verify a closed itemset from tree structures, and avoid checking whether it is subsumed by some already found closed itemset with identical support. From experimental results we can learn that the search space can be pruned efficiently, and the verifying process is improved. 6. CONCLUSIONS In this paper, we have proposed an efficient algorithm named CloHUI for more efficiently mining CHUIs from transaction databases. A novel data structure HUITWU-Tree was proposed for maintaining the information of itemsets in a database. Moreover, we developed an efficient strategy to verify a closed itemset faster. In CloHUI, closed itemsets are first computed. If an itemset is closed, its utility in the database can be calculated directly from a HUITWU-Tree and a utility database. Compared with the method generating candidates first and then computing the utilities of the candidates in the database, the performance of our proposed algorithm is enhanced significantly. In the experiments, both of synthetic and real datasets were used to evaluate the performance of CloHUI. The experimental results showed that for dense datasets our proposed algorithm is an order of magnitude faster than the state-of-the-art algorithm CHUD, and consumes less memory. For sparse datasets, CloHUI outperforms CHUD in terms of runtime. ACKNOWLEDGEMENTS This work is partly supported by the National Natural Science Foundation of China under Grant Nos. 61190115 and 61173022. REFERENCES [1] Han J, Cheng H, Xin D et al. (2007) Frequent pattern mining: current status and future directions, Data Min. Knowl. Discov., Vol. 15, No. 1, pp55-86. [2] Yao H, Hamilton H J (2006) Mining itemset utilities from transaction databases, Data Knowl. Eng., Vol. 59, No. 3, pp603-626. [3] Yao H, Hamilton H J, Butz C J (2004) A foundational approach to mining itemset utilities from databases, In Proc. the 4th SIAM Int. Conf. Data Min., pp482-486. [4] Ahmed C F, Tanbeer S K, Jeong B S et al. (2009) Efficient tree structures for high utility pattern mining in incremental databases, IEEE Trans. Knowl. Data Eng., Vol. 21, No. 12, pp1708-1721. [5] Tseng V S, Wu C W, Shie B E et al. (2013) Efficient algorithms for mining high utility itemsets from transactional databases, IEEE Trans. Knowl. Data Eng., Vol. 25, No. 8, pp1772-1786. [6] Liu Y, Liao W, Choudhary A (2005) A two-phase algorithm for fast discovery of high utility of itemsets, In Proc. the 9th Pacific-Asia Conf. Knowl. Discov. Data Min., pp689-695. [7] Tseng V S, Wu C W, Shie B E et al. (2010) UP-Growth: an efficient algorithm for high utility itemset mining, In Proc. the 16th ACM Conf. Knowl. Discov. Data Min., pp253-262. [8] Liu M C, Qu J F (2012) Mining high utility itemsets without candidate generation, In Proc. the 21th ACM Conf. Inf. Knowl. Man., pp55-64. [9] Wu C W, Philippe F V, Yu P S et al. (2011) Efficient mining of a concise and lossless representation of high utility itemsets, In Proc. the 11th IEEE Conf. Data Min., pp824-833. [10] Agrawal R, Srikant R (1994) Fast algorithms for mining association rules, In Proc. the 20th Conf. Very Large Data Bases, pp487-499. [11] Han J, Pei J, Yin Y (2000) Mining frequent patterns without candidate generation, In Proc. the 2000 ACM SIGMOD Conf. Man. Data, pp1-12. [12] Li Y X, Yeh J S, Chang C C (2008) Isolated items discarding strategy for discovering high utility itemsets, Data Knowl. Eng., Vol. 64, No.1, pp198-217. [13] Zihayat M, An A (2014) Mining top-k high utility patterns over data streams, Inf. Sci., Vol. 285, pp138-161. [14] Pei J, Han J, Mao R (2000) CLOSET: an efficient algorithm for mining frequent closed itemsets, ACM SIGMOD workshop Data Min. Knowl. Discov., pp21-30.](https://image.slidesharecdn.com/8516ijcsit08-161105043656/75/CLOHUI-AN-EFFICIENT-ALGORITHM-FOR-MINING-CLOSED-HIGH-UTILITY-ITEMSETS-FROM-TRANSACTION-DATABASES-19-2048.jpg)
