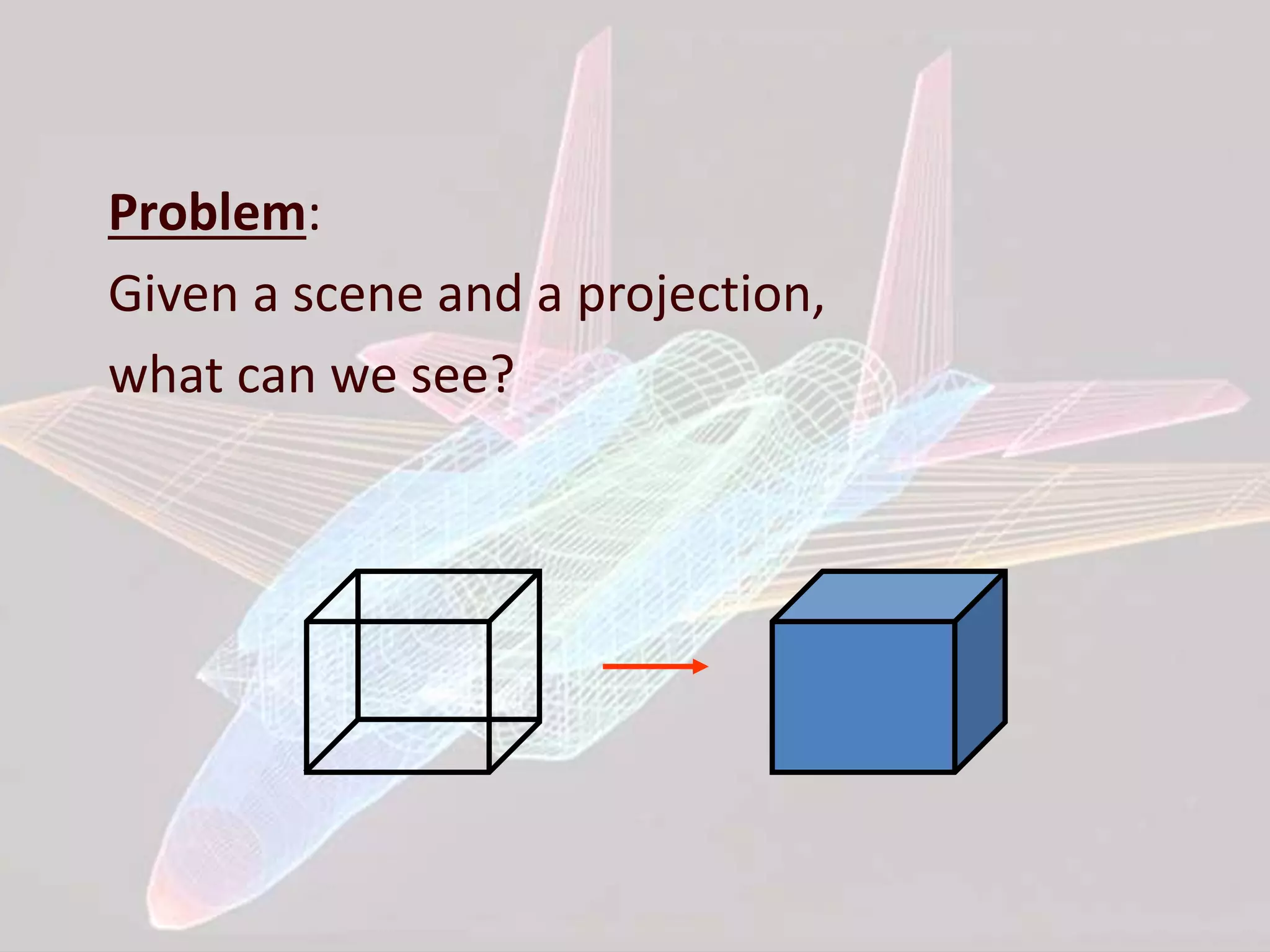
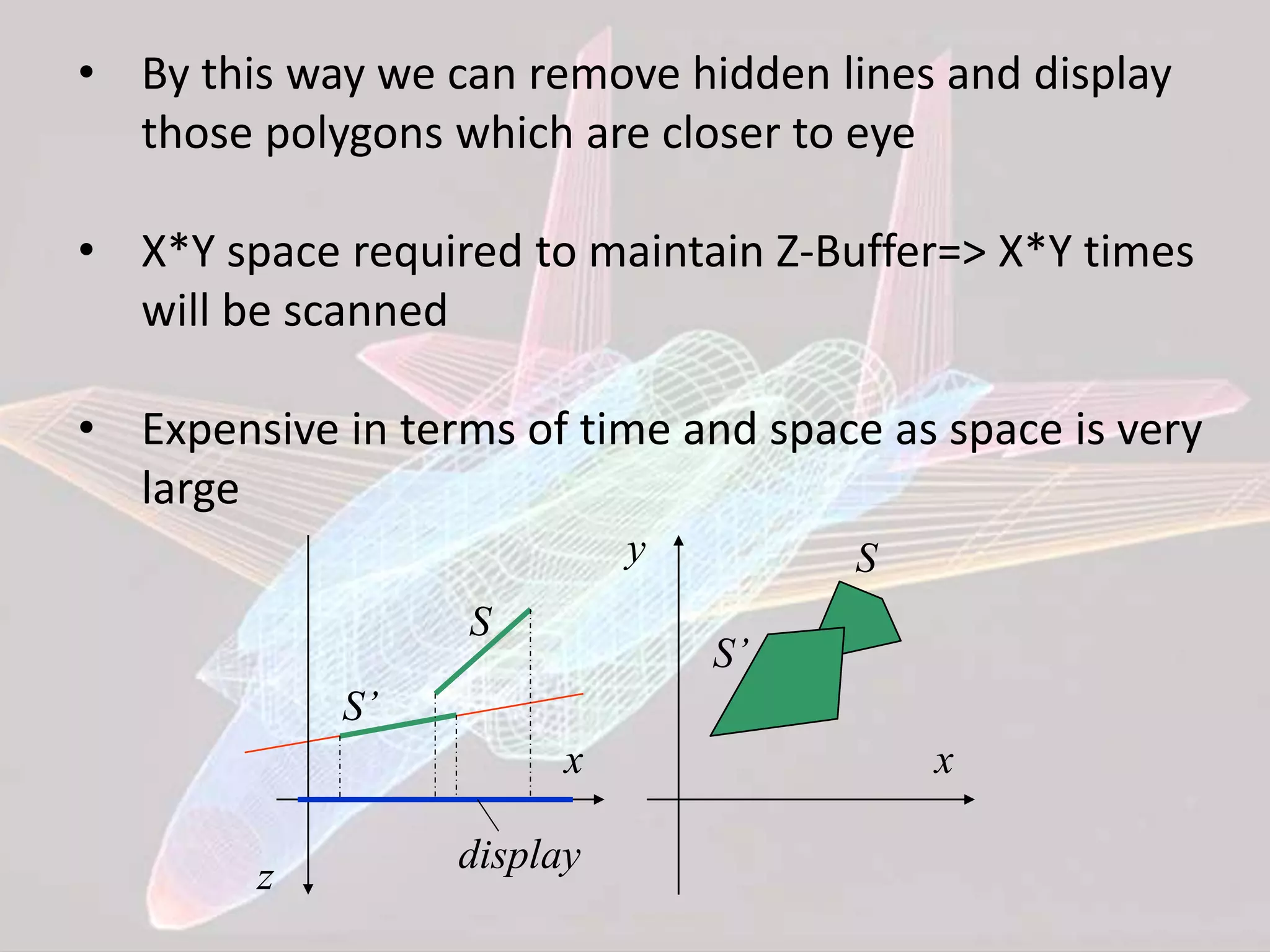
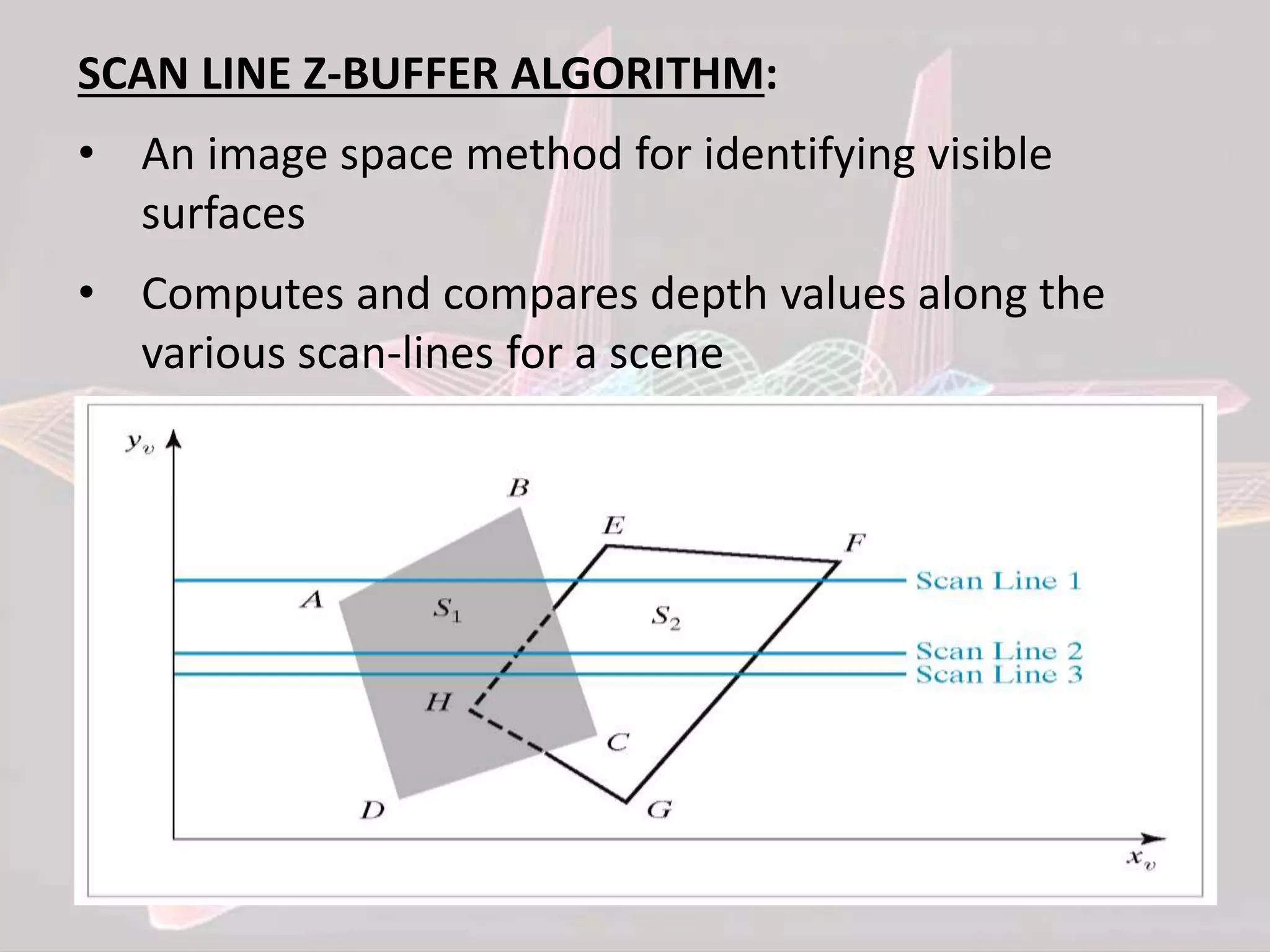
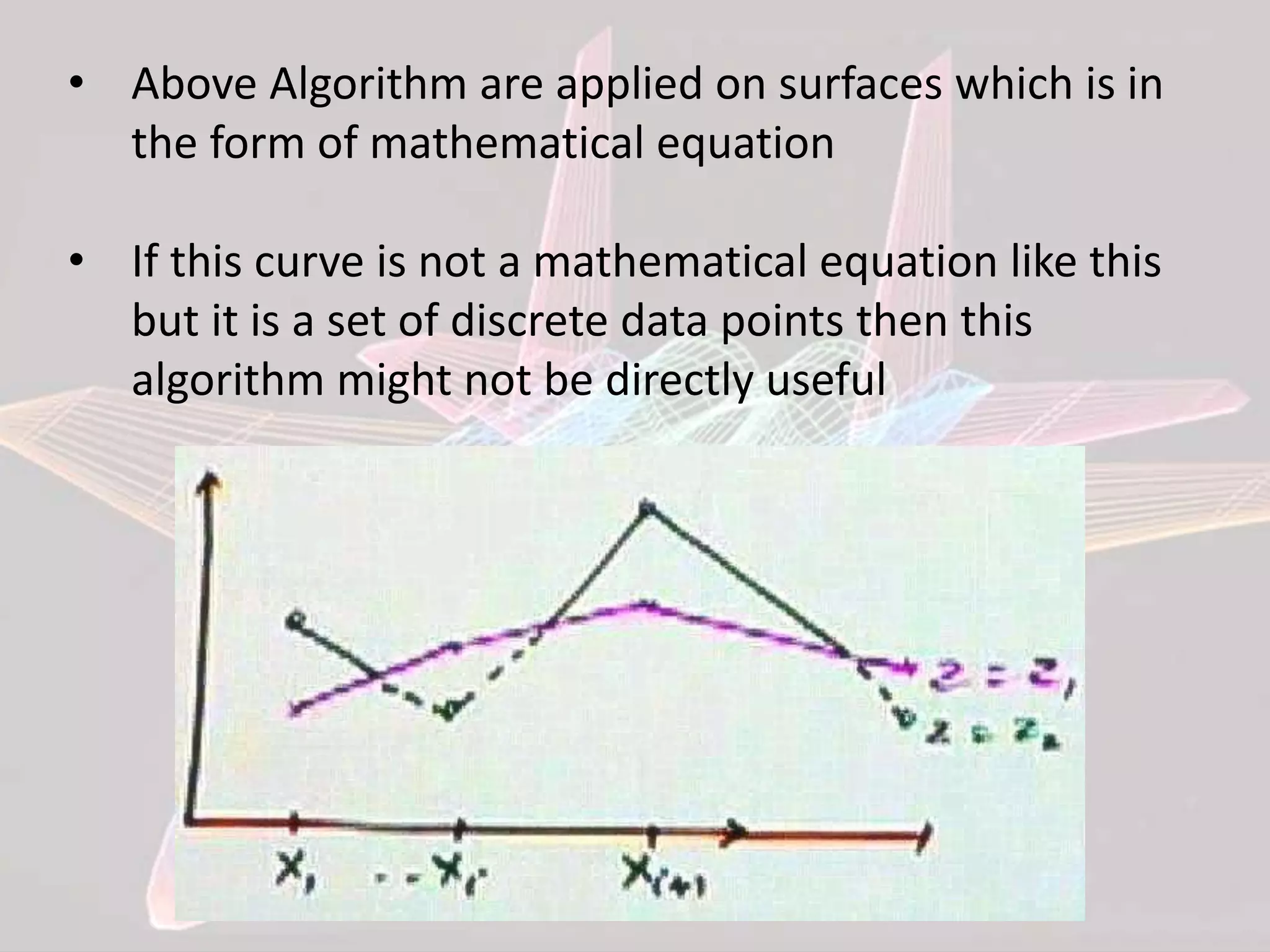
This document discusses various algorithms for hidden surface removal when rendering 3D scenes, including the z-buffer method, scan-line method, spanning scan-line method, floating horizon method, and discrete data method. The z-buffer method uses a depth buffer to track the closest surface at each pixel. The scan-line method only considers visible surfaces within each scan line. The floating horizon method finds the visible portions of curves using a horizon array. The discrete data method handles surfaces defined by discrete points rather than mathematical equations.




![Z-BUFFER ALGORITHM: • Its an extension of Frame Buffer • Display is always stored on Frame Buffer • Frame Buffer stores information of each and every pixel on the screen • Bits (0, 1) decide that the pixel will be ON or OFF • Z- Buffer apart from Frame buffer stores the depth of pixel • After analyzing the data of the overlapping polygons, pixel closer to the eye will be updated • Resolution of X,Y => Array[X,Y]](https://image.slidesharecdn.com/cghlrappt-150601180631-lva1-app6892/75/Computer-Graphics-Hidden-Line-Removal-Algorithm-6-2048.jpg)






![1 2 3 4 5 6 Each span at most one polygon shall be displayed • For each polygon determine the highest scan line intersected by it • Place the polygon in the Y-Bucket of that scan line [YB] • For each scan line -Examine YB for any new polygon -Add new polygon to APL -Update AEL -Divide into spans -In each span decide which polygon shall be displayed -Increment Y, update AEL & APL](https://image.slidesharecdn.com/cghlrappt-150601180631-lva1-app6892/75/Computer-Graphics-Hidden-Line-Removal-Algorithm-15-2048.jpg)
![FLOATING HORIZON ALGORITHM: • Used for displaying surface • Take each plane & intersection z=constant plane and get a curve from F(x,y)=0 f(x,y,z)=0 Array HORIZONTAL[X]=Ymax Curve in each plane=>f(x,y)=0 y=f(x,y) z=constant curves Family of curves](https://image.slidesharecdn.com/cghlrappt-150601180631-lva1-app6892/75/Computer-Graphics-Hidden-Line-Removal-Algorithm-16-2048.jpg)

![• Maintain HORIZON[X] at each side • While displaying next curve, it will be compared to 2 points i.e, Y(Xi) & Y(Xi+1) • If both points are visible, then the complete curve is visible • Algorithm will be complex as the curve is in discrete data form Y(Xi) Y(Xi+1) Result V V Curve is visible V I Xi to Intersection -> Visible Intersection to Xi+1 -> NOT Visible I V Xi to Intersection -> NOT Visible Intersection to Xi+1 -> Visible I I NOT Visible](https://image.slidesharecdn.com/cghlrappt-150601180631-lva1-app6892/75/Computer-Graphics-Hidden-Line-Removal-Algorithm-19-2048.jpg)


