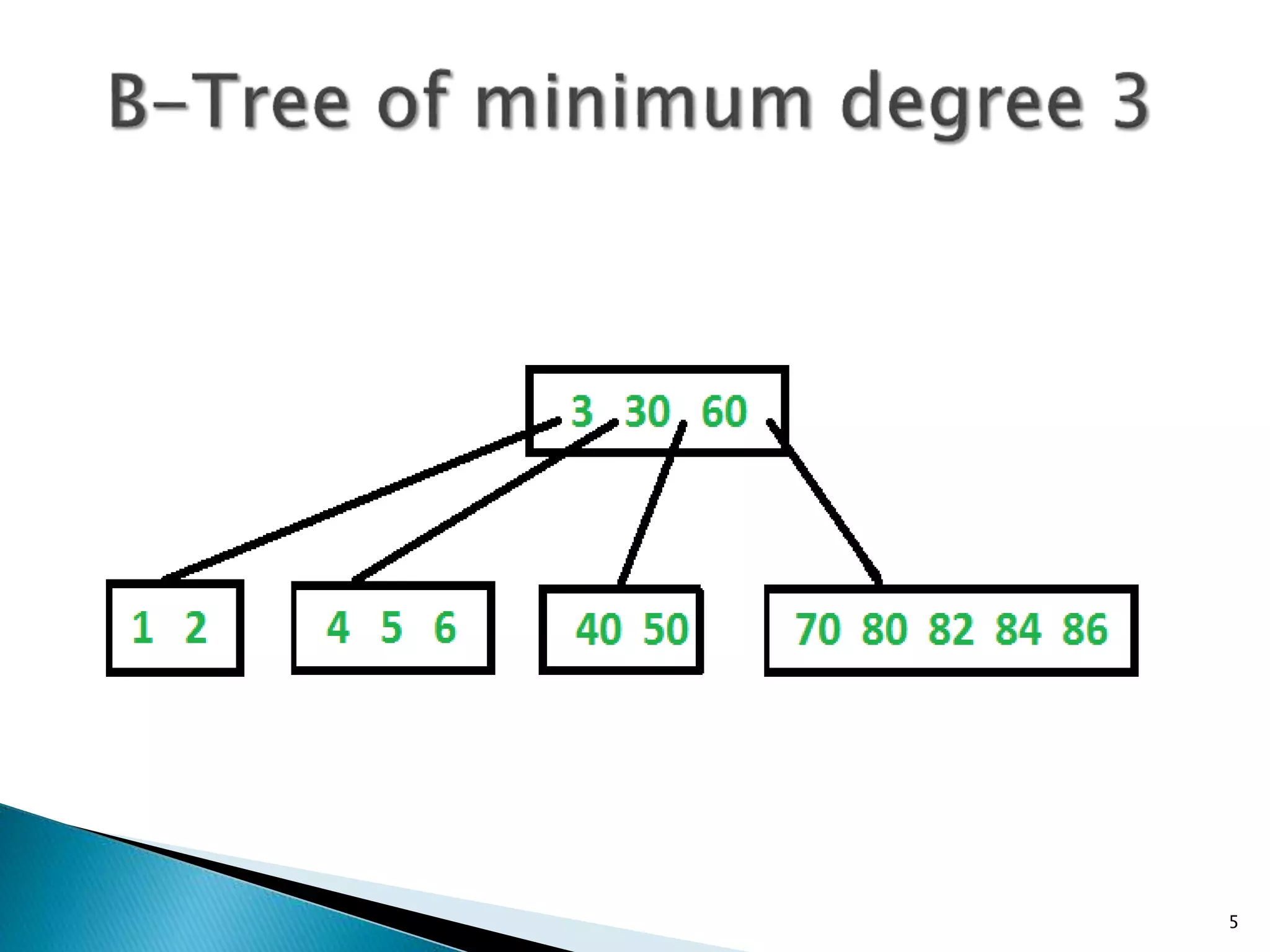
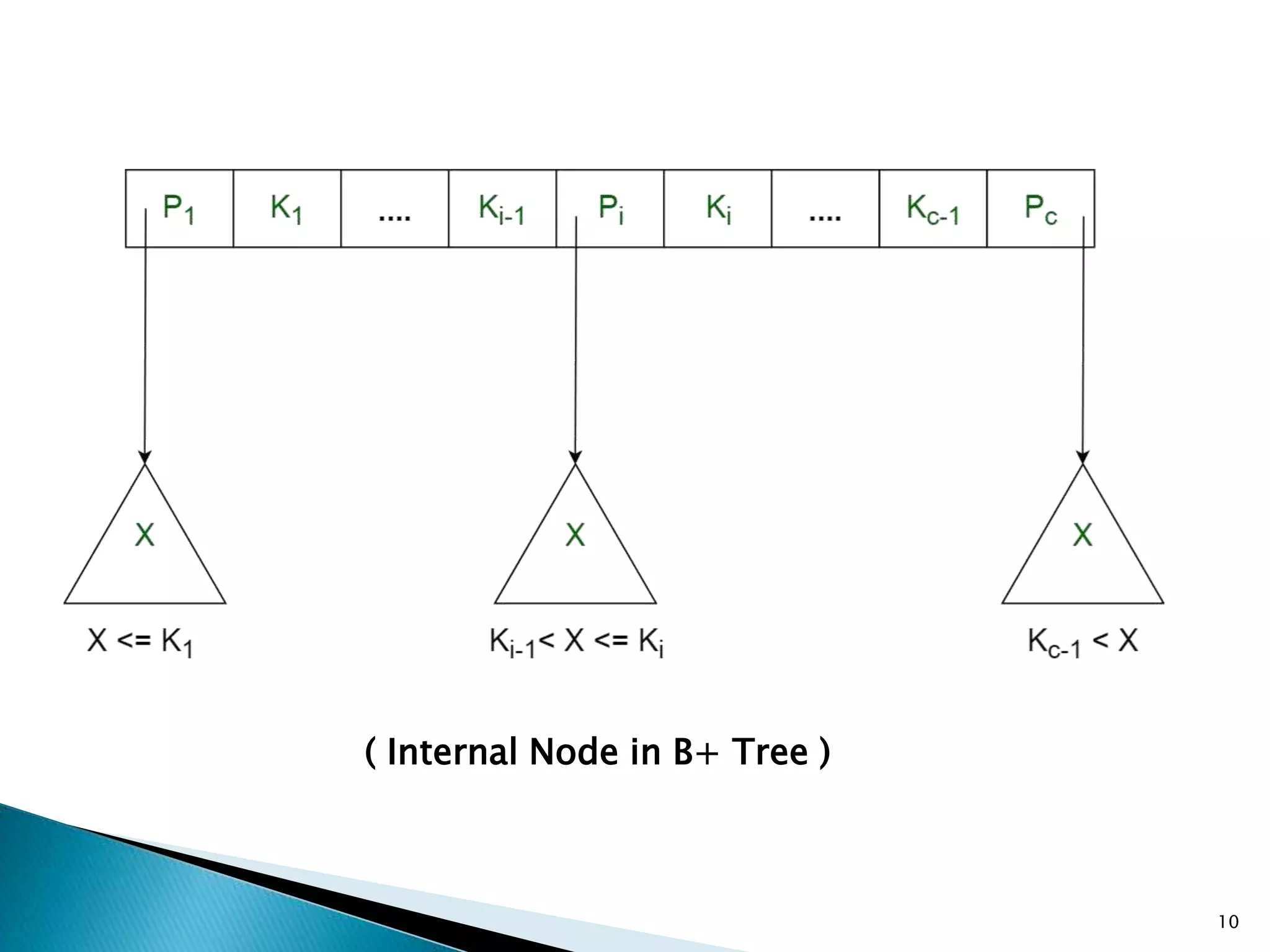
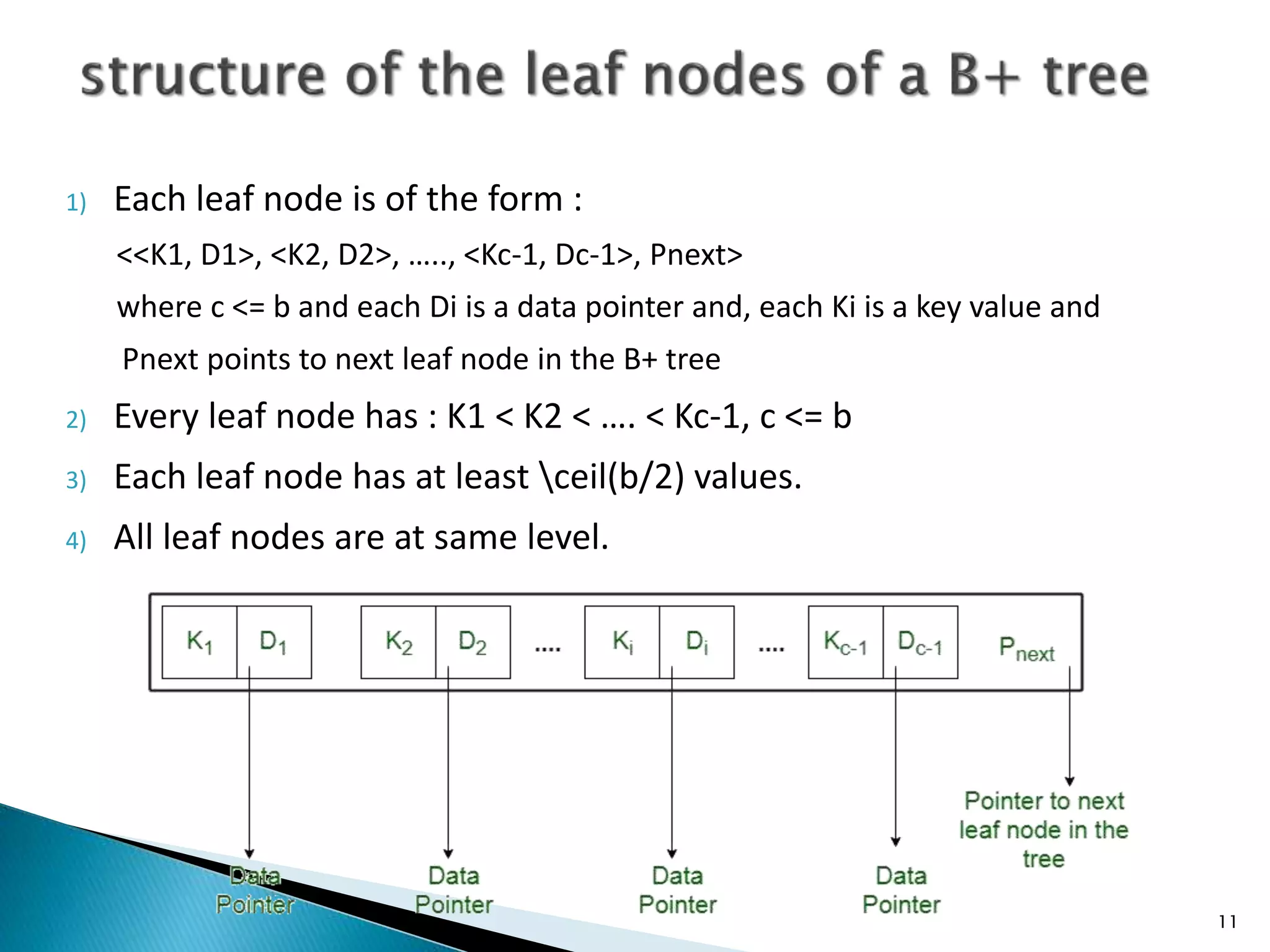
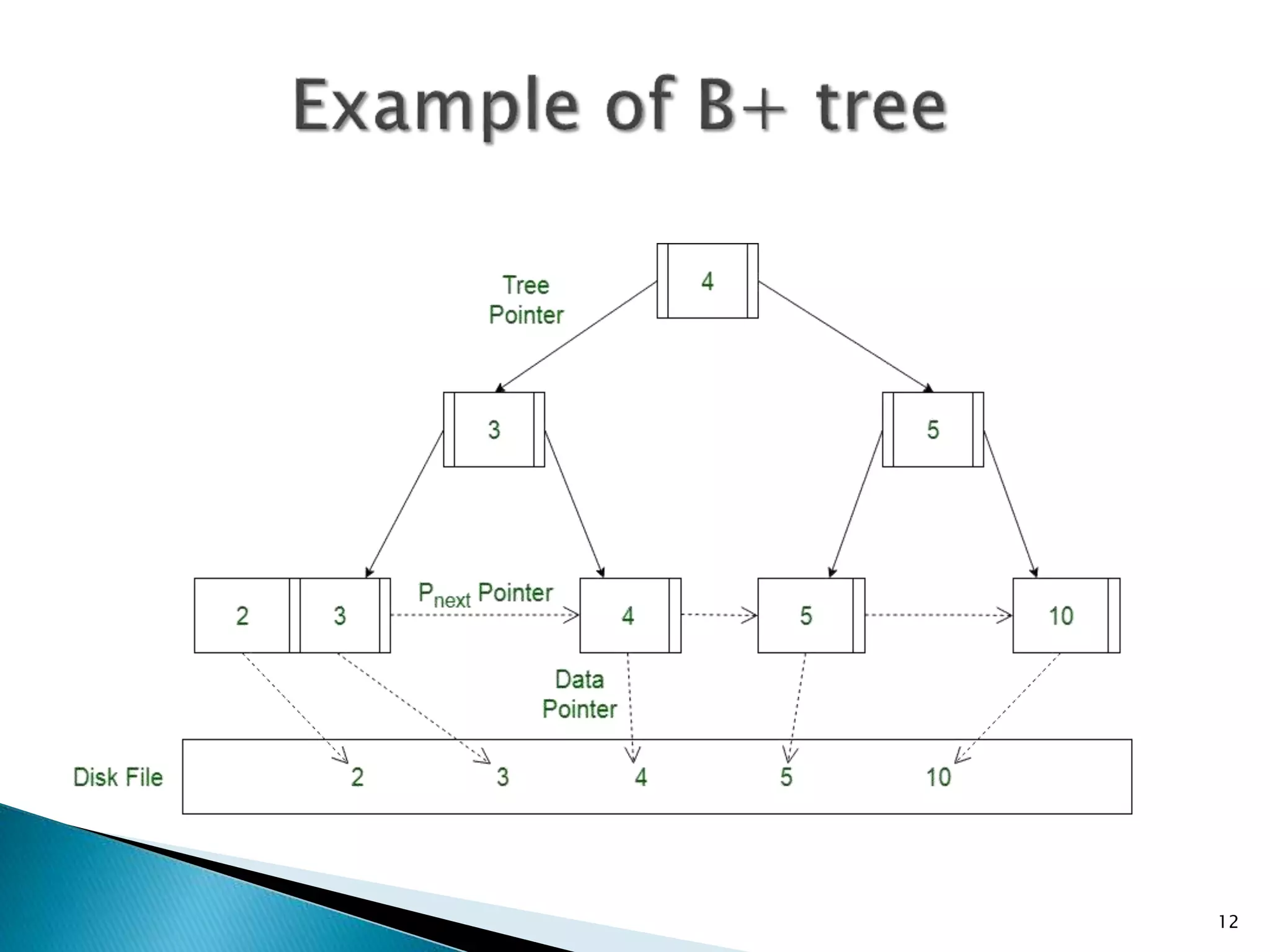
The document discusses B-trees and B+ trees, which are self-balancing search trees designed to minimize disk access time during data retrieval. B-trees store keys and data pointers at all nodes, while B+ trees store data pointers only at the leaf nodes, facilitating a more efficient indexing structure. Both structures maintain low height and balance by maximizing the number of keys per node, ensuring optimal performance in data operations.