Empirical Coding for Curvature Based Linear Representation in Image Retrieval System

IOSR Journal of Computer Engineering (IOSR-JCE) e-ISSN: 2278-0661,p-ISSN: 2278-8727, Volume 17, Issue 3, Ver. VI (May – Jun. 2015), PP 05-16 www.iosrjournals.org DOI: 10.9790/0661-17360516 www.iosrjournals.org 5 | Page Empirical Coding for Curvature Based Linear Representation in Image Retrieval System Dayanand Jamkhandikar1 , Dr. Surendra Pal Singh2 , Dr.V. D. Mytri3 1 (Research Scholar, CS&E Department, Nims Institute of Engineering and Technology, NIMS University, Jaipur, India) 2 (Assoc. Professor, CS&E Department, Nims Institute of Engineering and Technology, NIMS University, Jaipur, India) 3 (Principal, Appa Institute of Engineering and Technology, Gulbarga, India) Abstract : Image retrieval systems are finding their applications in all automation systems, wherein automated decision needs to be taken based on the image contents. The prime requirement of such systems is to develop a very accurate coding system for maximum retrieval accuracy. Due to the processing error or surrounding errors the efficiency of such systems is reduced, so for the optimization of recognition efficiency, a linear coding for curvature based image recognition system is developed. This paper presents an approach of linear representation of curvature scale coding for an image shape descriptor. In this approach, an average curvature scale representation is done and an empirical modeling of signal decomposition is applied for feature description. In the process of empirical feature description, a spectral density based coding approach is also proposed for the selection of descriptive shape information from the extracted contour regions. This approach is named as Linear Curvature Empirical Coding (LCEC) which is simpler to derive shape features from curvature information based on linear signal representation and coding. The results show that our proposed approach performs better in comparison with previous known approaches. Keywords: Empirical Signal Decomposition, Curvature Scale Coding, Linear Curvature Empirical Coding, CBIR. I. Introduction In the process of image recognition various approaches of image representation and coding were developed. Image recognition has emerged into new area of applications, such as e-learning, medical diagnosis, authentication and security, mining, industrial applications etc. With development of new technologies in imaging, images are now captured at very high resolutions, and each detail of the image could be extracted at a very finer level to represent the image. However the representing coding, such as shape, color, textures was extracted from the content based on feature descriptors used. It is hence observed that the performance of an image retrieval system mainly depends on the representing features. Among all these representative features, shape is observed to be a simpler and distinct representative feature for an image sample. To derive the shape feature edge based feature descriptors were proposed. In [1] an optimal edge based shape detection using the approach of derivative of the double exponential (DODE) function is proposed. The approach is a enhance modeling of image shape representation, wherein a DODE filter is applied over the bounding contour to derive exact shape of an image. In [2] to derive edge features, a combination of invariant moments and edge direction histogram is proposed. In various approaches, moments are used as a shape descriptor to define the shape feature. In [3] an angular radial transform (ART) descriptor, for MPEG-7 region-based shape description is proposed. This ART descriptor is defined as a ICA Zernike moment shape descriptor and the whitening Zernike moment shape descriptor for image shape representation. Where in edge based approaches are the simplest mode of shape representation, in most of the image representation, edge operators derive coefficients out of the bounding regions. These extra information’s result in computational overhead. Hence, results in slower system process. To derive more precise shape description, contour based codlings were developed. A contour based learning approach is defined in [4]. The approach of contour is a bound region growing method where the outer bounding region is extracted via a region growing approach to derive image representation. In [5], a binary image is decomposed into a set of closed contours, where each contour is represented as a chain code. To measure the similarity between two images, the distances between each contour in one image and all contours in the other are computed using a string matching technique. Then, a weighted sum of the average and maximum of these distances constitutes the final similarity. The methods of the contour-based are mainly Polygonal approximation, Fourier descriptors [6], wavelet descriptors, or scale space [7, 8], wherein the region-based methods are mainly geometric moment invariants, and orthogonal moments [9]. In addition to the edge and contour based coding various other approaches such as in [10], a graph structure, called concavity graph, representing multi object images using individual objects and their spatial relationships is proposed. In [11] a

Empirical Coding for Curvature Based Linear Representation in Image Retrieval System DOI: 10.9790/0661-17360516 www.iosrjournals.org 6 | Page very efficient shape descriptor called shape context (SC) was developed. This descriptor defines a histogram based modeling is proposed for the attached coefficient of each boundary point describing the relative distribution of the remaining points to that point. In [12] a polar transformation uses the shape points about the geometric center of object, the distinctive vertices of the shape are extracted and used as comparative parameters to minimize the difference of shape distance from the center. In [13], a retrieval method based on local perceptual shape descriptor and similarity indexing is proposed. A local invariant feature called ‘SIFT’ (Scale- invariant feature transform) [14], which compute a histogram of local oriented gradients around the feature point is proposed. However the contour based or the other techniques such as graph based, context based etc. defines the overall bounding contour, wherein the variations in the feature coefficients are very large. Each projection in the contour region is taken as a feature, which leads to large feature data set. To overcome the problem of large feature vectors, curvature coding has emerged in recent past. A curvature based scale space representation is presented in [3]. A very effective representation method was proposed that makes use of both concavities and convexities of all curvature points [6]. It is called multi scale convexity concavity (MCC) representation, where different scales are obtained by smoothing the boundary with Gaussian kernels of different widths. The curvature of each boundary point is measured based on the relative displacement of a contour point with respect to its position in the preceding scale level. The approach of curvature coding, results in lower feature descriptors for image retrieval. However in such coding, features are extracted based on a thresholding of the curvature plot, and values with higher magnitude are selected. This approach of feature selection process discards the lower variational information considering as noise. However in various image samples curvature with variations existing for a lower time period exist. So, this assumption of feature selection process minimizes the descriptive features relevancy with respect to image representation. To overcome this issue, in this paper a new coding approach, by the linearization of curvature coding and normalization process is proposed. The linearization process results in the representation of curvature information into a 1-D plane, which is then processed for feature representation, based on Empirical coding. This proposed approach improves the selection of feature relevancy, in terms of selectivity, where features are selected based on variational density rather to magnitudes. To present the stated work, this paper is presented in 6 sections. Wherein, section 2 outlines the modeling of an image retrieval system. The geometrical features for image representation are presented in section 3. The conventional approach of curvature based coding for image retrieval is presented. Section 4 presents the approach of proposed LCEC approach for image retrieval. The evaluation of the developed approach is presented in section 5. The concluding remark is presented in section 6. II. Image Retrieval System In the process of image retrieval various coding approaches were developed in past. These developed approaches were developed based on the content information’s of the sample. Such systems are termed as content based image retrieval (CBIR) system. A lot of research has been carried out on Content based image retrieval (CBIR) in the past decade. The goal of CBIR systems is to return images or its information’s, which are similar to a query image. Such system characterizes images using low-level perceptual features like color, shape and texture and the overall similarity of a query image with data base images. Due to rapid increase in amount of digital image collections, various techniques for storing, browsing, retrieving images have been investigate in recent years. The traditional approach to image retrieval is to interpret image by text and then use text based data base management system to perform image retrieval. The image retrieval systems are computed with basically the content features of the image namely color, or shape recognition. To achieve the objective of image retrieval, the operation is performed in two operational stages, training and testing. A Basic operational architecture for such a system is shown in figure 1. Figure 1: A Basic model of content based image retrieval system

Empirical Coding for Curvature Based Linear Representation in Image Retrieval System DOI: 10.9790/0661-17360516 www.iosrjournals.org 7 | Page In such system the samples are preprocessed for filtration, and dimensional uniformity. The preprocessed samples were then processed for feature extraction. These features are the descriptive details of each test sample or training sample which are stored onto dataset for further processing. The accuracy of these feature descriptors defines the processing accuracy of the system. III. Geometrical Shape Descriptor In the process of feature extraction, to retrieve geometrical feature information’s, edge descriptors were used. Edge descriptors were defined to represent the image information in 2 logical levels representing, high or low based on the bounding regions pixel magnitude. Edge information’s were then used to derive the regions content for which feature extraction process is carried out. An Edge based coding approach for image retrieval application is presented in [1]. However in the process of edge based coding the discontinuous edge regions reflects in discard of image regions or the inclusion of such regions increases the number of processing regions. This intern increases the overhead of feature extraction, number of feature coefficients and reduces the retrieval performance. To overcome the limitation of region selection on edge coding, curvature based coding were developed. This approach is observed to be more effective in region extraction based on the closed bounding regions, termed as contours. The approach of contour based curvature coding, were also applied to image retrieval. In [4, 6] a curvature coding approach is proposed. The coding approach derives all the concavity and connectivity of a contour region by the successive smoothening of contour region using a Gaussian filtration kernel. A multi scale curvature coding termed MCC is defined for such coding. The approach present an approach to curvature coding based on 8-negihbour hood region growing method for contour extraction and region representation. A bounding corner point for the contour is used as shape descriptor in this approach. To derive the curvature points in such approach a contour coding is defined, over which a curvature based coding is developed. In the process of contour coding, with defined constraints contours were extracted. For the detection of contour evaluation all the true corners should be detected and no false corners should be detected. All the corner points should be located for proper continuity. The contour evaluator must be effective in estimating the true edges under different noise levels for robust contour estimation. For the estimation of the contour region an 8-region neighborhood-growing algorithm is used [20, 21]. The process of contour evolution process is depicted in figure 2. Figure 2: Tracing operation in contour evolution. To the derived contour coordinates (x (u), y(u)) a curvature coding is applied to extract the shape features, defining dominant curve regions. The curvature of a curve is defined as the derivative of the tangent angle to the curve, consider a parametric vector equation for a curve [15, 22]; given by eqn.(1) ... (1) Where u is an arbitrary parameter. The formula for computing the curvature function can be expressed as the curvature, ‘K’, for given contour coordinates is defined by the eqn.(2) ... (2) Where are first derivative and are the double derivative of x and y contour co-ordinates respectively.

Empirical Coding for Curvature Based Linear Representation in Image Retrieval System DOI: 10.9790/0661-17360516 www.iosrjournals.org 8 | Page This curvature represents the curvature pattern for the extracted contour. A smoothening of such contour reveals in the dominant curvature patterns, which illustrates the representing shape of the region. Hence to extract the dominant curvature patterns, the obtained curvature is recursively smoothened by using Gaussian smoothening parameter (σ). The Gaussian smoothening operation is then defined by eqn.(3), ( , ) ( ) ( , ) ( , ) ( ) ( , )X u x u g u Y u y u g u       … (3) Where, g(u, σ) denotes a Gaussian of width ‘σ’ defined by eqn.(4), 2 2 2 1 ( , ) 2 u g u e       … (4) The curvature ‘K’ is then defined by the eqn.(5) as;   3/22 2 ( , ) ( , ) ( , ) ( , ) ( , ) ( , ) ( , ) u uu uu u u X u Y u X u Y u k u X u Y u           … (5) Figure 3 shows the process of smoothening and the application of smoothening factor ‘σ’. Figure 3: Smoothening process for a curvature at different smoothening factors. These curvatures are stored as a measuring parameter defining, shape of the image. A plot of coordinate over the derived curvature coordinate is defined as the curvature scale space image (CSS) [15,22]. A CSS explores the dominant edge regions in an image, wherein curvature having higher dominance will be presented for a longer time than the finer edge regions. A threshold approach is then applied over this CSS curve to pick the defining features, and edge coefficients which are extracted over the threshold are used as feature descriptor. A CSS plot and the process of feature selection are as shown in figure 3. Figure 4: CSS plot and process of thresholding A CSS representation of a given query sample is illustrated in figure 4. (p1,k1),(p2,k2),…… (pn,kn) are the extracted feature values used as image descriptor. However, in such a coding process, information’s below the threshold is totally neglected. This elimination is made based on the assumption that, only dominant edges exist for longer duration of smoothing and all the lower values are neglected treating as noise. For example, for a given CSS plot for a query sample, the region below the threshold is considered to be non-informative and totally neglected. This consideration leads to following observations; 1) Under semantic objects having similar edge representation, a false classification will appear. 2) Information’s at lower regions also reveals information of images having shorter projections such as spines. 3) Direct elimination of the entire coefficient leads to information loss as well, a random pickup will leads to higher noise density. These problems are to be overcome to achieve higher level of retrieval accuracy in spatial semantic samples, or with sample having finer edge regions. To achieve the objective of efficient retrieval in semantic observations, a

Empirical Coding for Curvature Based Linear Representation in Image Retrieval System DOI: 10.9790/0661-17360516 www.iosrjournals.org 9 | Page linear curvature Empirical coding (LCEC) is proposed. The proposed approach is as outlined in following section. IV. Linear Curvature Empirical Coding (LCEC) It could be observed that the obtained CSS plot represents the edge variations over different smoothing factors. This CSS representation appears as a 1-D signal with random variations. Taking this observation in consideration, a linear representation of the curvature coding for feature representation is proposed. For the linearization of the CSS curve, a linear sum of the entire curvature plane at different Gaussian smoothening actor is taken. The linear transformation is defined by eqn.(6) as, Ls = … (6) Where, Ls is the linearized signal, and Ki is the obtained curvature for ith value of σ. 0 50 100 150 200 250 300 350 400 1 2 3 4 5 6 7 8 9 10 11 Time Magnitude 1-D Signal representtion Figure 5: Linearized representation of a CSS plot A linearized signal representation for a CSS plot is as shown in figure 5. This signal represents all the variations present from the lower smoothening to the highest smoothening factor. Among all these variations, it is required to extract the required variation coefficient, which best represent the image shape. To extract the optimal peak points, an empirical coding is developed. In the process of empirical coding, the linearized signal Ls is decomposed into intermediate frequency components using the approach of Empirical mode decomposition (EMD) [16]. Empirical mode decomposition (EMD) is a very popular and effective tool in the area of speech [17], image [18] and signal processing [19]. Various applications were developed using the approach of EMD for the enhancement of input sample, such as speech denoising, jitter elimination, or noise reduction. EMD is processed in a nonlinear manner for analysis of non-stationary signals. EMD decompose the time domain signal into a set of adaptive basis functions called intrinsic mode function (IMF). The IMF is formulated as the oscillatory components of the signal with no DC element. In the process of decomposition, tow extreme are extracted and high frequency components are selected between these two points. The left out are defined as the low frequency components. This process is repeated over the residual part repetitively to derive n-IMFs reflecting different frequency elements. A signal x(n) is represented by EMD as eqn.(7), … (7) Where, is the residual component. The IMFs are varied from high frequency content to low frequency content with increase in IMF order. The proposed Algorithm for LCEC is as outlined; Algorithm LCEC: Input: linear curvature, Output: Feature vector, sfi Step 1: Perform EMD computation for the obtained Linear Curvature signal. Compute EMD by following step a-f: Step a: compute the Local maxima(Xmax) and local minima(Xmin) for linear curvature sequence x[n] Step b: compute minimum and maximum envelop signal, emin and emax. Step c: Derive the mean envelop m[n]. Step d: Compute the detail signal d[n]. Step e: Validate for Zero mean stopping criterion. Step f: Buffer data as IMF or residuals, from the derived detail signal.

Empirical Coding for Curvature Based Linear Representation in Image Retrieval System DOI: 10.9790/0661-17360516 www.iosrjournals.org 10 | Page Step 2: For obtained IMFs compute spectral density of each IMF using PSD. Step 3: Select two IMFs having highest energy density (I1, I2). Step 4: Compute threshold limit for I1, I2 as 0.6 of max(Ii). Step 5: Derive the feature vectors (sfi) from these two IMFs for classification. The operational flow chart for the EMD based decomposition is summarized in figure 6. 0 50 100 150 200 250 300 350 400 -20 0 20 imf1 0 50 100 150 200 250 300 350 400 -10 0 10 imf2 0 50 100 150 200 250 300 350 400 -5 0 5 imf3 0 50 100 150 200 250 300 350 400 -2 0 2 imf4 0 50 100 150 200 250 300 350 400 0 0.5 1 residual time Figure 6: Operational flow chart for EMD coding Figure 7: IMFs derived for the linearized signal An example for the obtained IMFs for the linearized signal of figure 4, is shown in figure 7. The obtained IMFs {I1 – I4} are the decomposed detail IMFs reveling different frequency content at each level. At each decomposition level the residual IMF, r[n], is decomposed in each successive IMF to obtain finer frequency information’s. Each obtained IMF, reveals a finer frequency content and based on the density of these frequency contents, then a decision of feature selection is made. This approach of feature selection, results in selection of feature details, at lower frequency resolutions also, which were discarded in the conventional CSS approach. To derive the spectral density of these obtained IMFs, power spectral densities (PSD) to the obtained IMFs are computed. PSD is defined as a density operator which defines the variation of power over different content frequencies, in a given signal x(t). The Power spectral density (PSD) for a given signal x(t) is defined by eqn.(8) as, … (8) Taking each IMF ‘Ii’ as reference, a PSD for each IMF, ‘PIi’ is computed. The PSD features for the four obtained IMFs are then defined by eqn.(9) , PIi = PSD (Ii), for i = 1 to 4 … (9) The IMF PSD’s are derived as eqn.(10) , … (10) From these obtained energy values, IMFs are selected based on a defined selection criterion, as outlined,

Empirical Coding for Curvature Based Linear Representation in Image Retrieval System DOI: 10.9790/0661-17360516 www.iosrjournals.org 11 | Page for the obtained PIi, maximum PI is computed as given under, MPIi = max(PIi) For i =1 to 4 if (PIi ≥ (MPIi / 2)) sel_Ii = Ii, end For these selected IMFs, ‘Sel_Ii’ features are then computed by the approach of peak picking, as carried out in CSS approach. For each select IMF a maximum value is computed and all the coordinates above 60% of the pick value are taken as shape features ‘sfi’. With this approach the finer frequency contents which were discarded in the CSS approach, were also given consideration for feature extraction. These approaches hence derive more informative feature information than CSS. To evaluate the developed approach a simulation model of the proposed approach is developed. The system architecture for the proposed approach is shown in figure 8. Figure 8: System Architecture for the proposed approach The developed approach is carried out in two operation stages, training and testing. Wherein, training process set of recorded images are processed in a sequence and the process of feature extraction is performed. For each of the training image, the obtained features are buffered into an array termed as knowledge data base. During the process of querying the same process is repeated over the test sample and the obtained query feature is passed to a classifier to retrieve information’s from the knowledge data base. For the process of classification, a k-Nearest Neighbors (K-NN) classifier is used. The classifier is designed with a Euclidian distance based approach to obtain the best set of matches from the knowledge data base. The decision ‘D’ for the retrieval is derived as the minimum value of the Euclidian distance defined as eqn.(11) , … (11) Where, Euclidian Distance, … (12) Where, Q is the query feature and, dbfi is the features trained in the data base. To analyze the performance of this developed system an experimental analysis is carried out as presented below.

Empirical Coding for Curvature Based Linear Representation in Image Retrieval System DOI: 10.9790/0661-17360516 www.iosrjournals.org 12 | Page V. Experimental Results For the simulation of the proposed approach, ACER, leaf database MEW2010 [23], is used. This database was created for the experimental usage of recognition of wood species based on leaf shape. The data base consists of 90 wood species, for trees, and bushes. There are 2 to 25 samples for each species, with a total of 795 samples in the database. These samples were scanned by 300dpi scanner, and save in binarized format. Few of the samples of this data base are shown in figure 9. Figure 9: Training Database samples These test samples are passed to the processing algorithm for training, where each image is read in a sequence and the computed features are buffered in an array. This buffered information is taken as the knowledge information for classification. The process of proposed approach is carried out for a selected query sample. The processing results obtained are as illustrated below. Original Query Sample Extracted Edge Evolved Contour Figure 10: Query sample Figure 11: Extracted edge regions Figure 12: Extracted Contour regions For the evaluation of developed work, a randomly selected test query is passed to the developed system. The Selected test image sample is shown in figure 10. This sample is processed to retrieve similar details from the database stored. For the given test sample, an edge extraction process is carried out to find the bounding region for the given test sample. The extracted edge details are shown in figure 11. A Canny operator is used for the extraction of the edge details for the given test sample. By the usage of 8-neighbour region growing method, the contour evolution process is carried out. A bounding region for the obtained edge region is obtained, as shown in figure 12. The contour defines the defining shape region of a sample. In the figure illustrated it is observed that, for given sample the obtained contour, defines the shape of the feet region. Taking the contour evolved a curvature computation is made. The curvature obtained is represented in linear 1-D signal, as illustrated in below figure 13.

Empirical Coding for Curvature Based Linear Representation in Image Retrieval System DOI: 10.9790/0661-17360516 www.iosrjournals.org 13 | Page 0 100 200 300 400 500 600 700 1 2 3 4 5 6 7 Time Magnitude Linear Signal representtion 0 100 200 300 400 500 600 700 -4 -3 -2 -1 0 1 2 3 4 5 6 time(sec) magnitude(mv) initial IMF Figure 13: Linearized signal representation Figure 14: Initial IMF for the linearized signal of the curvature scale plot for the given sample To this derived Linear signal representation of the given test sample, the obtained curvature information’s are buffered in a linear array, and the coefficients are then considered as a 1-D linear signal elements to perform empirical decomposition to compute IMFs. The initial IMF for the linearized signal is shown in above figure 14. On the decomposition of the linearized signal, IMFs are obtained. In the initial IMF, the variations in the signals are highly concentric in this IMF. A successive decomposition is then carried out over the residual signal. 0 100 200 300 400 500 600 700 -10 0 10 imf1 0 100 200 300 400 500 600 700 -5 0 5 imf2 0 100 200 300 400 500 600 700 -10 0 10 imf3 0 100 200 300 400 500 600 700 -5 0 5 imf4 0 100 200 300 400 500 600 700 -5 0 5 imf5 0 100 200 300 400 500 600 700 -5 0 5 imf6 0 100 200 300 400 500 600 700 0 2 4 residual time(sec) 1 2 3 4 5 6 7 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 IMFs SpectralEnergyDensity Figure 15: IMFs for the linearized signal Figure 16: spectral Energy Density for Decomposed representation IMFs The 6 IMFs and the residual obtained are shown in above figure 15. It is observed that IMF 1 and IMF 3 exhibits higher coefficients variation than the other two bands, hence more curvature informations are presented in these two functions. To select the required IMFs for feature extraction, a spectral density using power spectral density is used. The energy density for each band is as shown in figure 16.The spectral energy density for each IMF is computed using, a power spectral density approach. Each IMF coefficients are averaged by the squared summation of its coefficients and energy is computed. From the IMF energy obtained, it is observed that, IMF 1 and 3 has comparatively higher energy density than the other two IMFs. This is observed to be synch with the observations made from the IMFs obtained as seen in above figure. Based on the energy derived, two highest energy density IMFs are selected, which is 1 and 3 in this case. Figure 17: Extraction of Features from Figure 18: Extraction of Features from selected IMF -1 selected IMF -3 Figure 17 and 18 shows the two selected IMFs for feature extraction. The features are selected based on the similar procedure of maximum thresholding approach as used in conventional MCC approach. For the two selected IMF, maximum peak values are found, and a threshold of 0.6 or the maximum peak is set as the

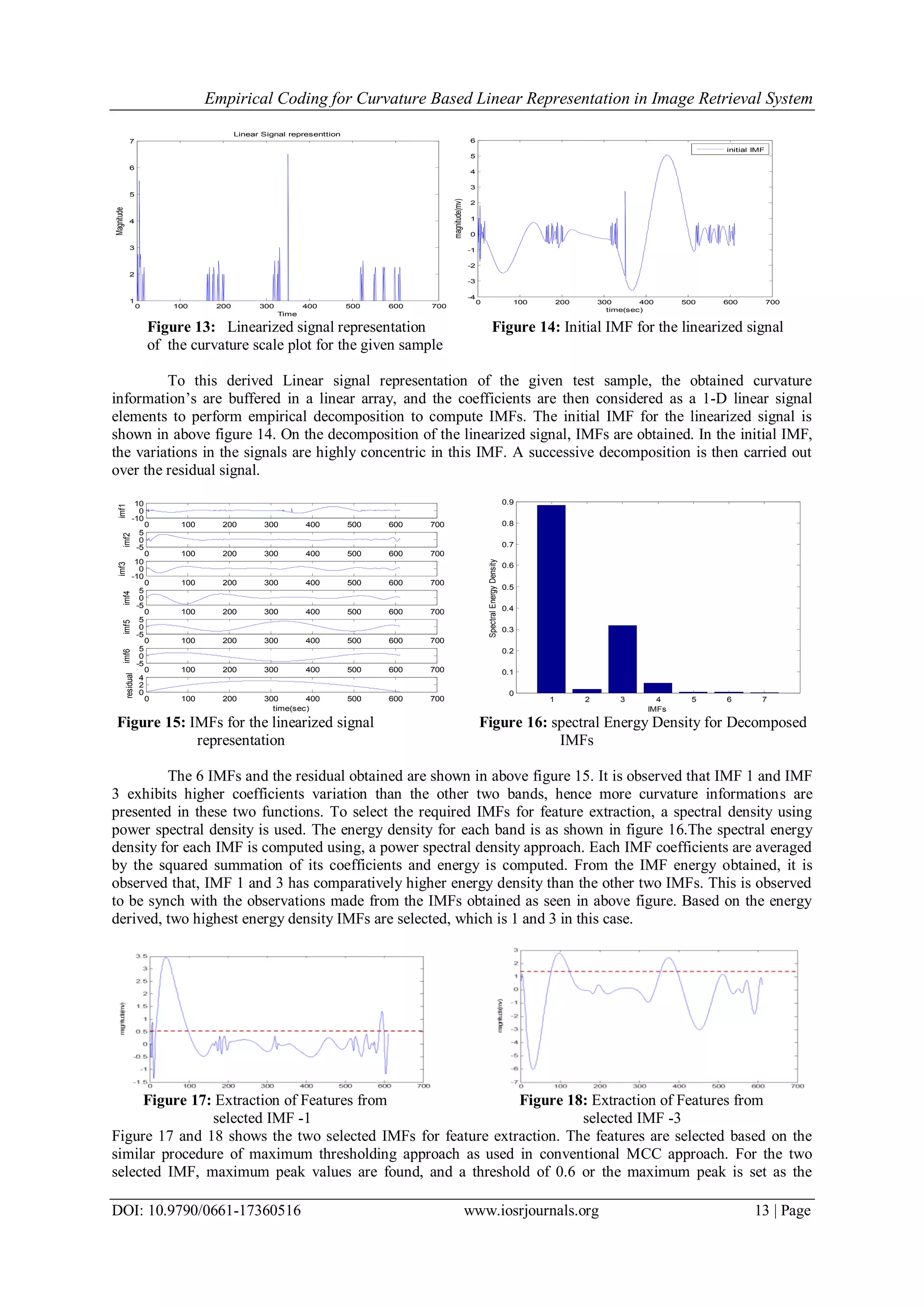
Empirical Coding for Curvature Based Linear Representation in Image Retrieval System DOI: 10.9790/0661-17360516 www.iosrjournals.org 14 | Page threshold value. All the peaks falling above to this threshold is recorded as the feature magnitude with its corresponding coordinates, recording dominant curvature peaks. The obtained feature values for the given test sample is recorded as, (3.5,50),(1.4,600),(2.9,99) and (2.3, 380). With these extracted features, a retrieval process is carried out for two test cases. The developed system is evaluated under two samples of different types, called dissimilar case, and two samples of spatially similar case, where the samples are observe to be visibly similar. This evaluation is carried out to analyze the performance of developed system retrieval performance under two distinct samples and two similar samples. The obtained results for the developed systems are as shown below. Original Query Sample Figure 19: Test Sample Top 3 classified Samples Using-Edge Reterived Sample-Edge (a) (b) Figure 20: (a) Top 3- classification for Edge Based [1] coding (b) Top retrieved sample Top 3 classified Samples Using-CONTOUR Reterived Sample-CONTOUR (a) (b) Figure 21: (a) Top 3- classification for contour Based [4,5] coding (b) Top retrieved sample Top 3 classified Samples Using-MCC Reterived Sample-MCC (a) (b) Figure 22: (a) Top 3- classification for MCC Based [6] coding (b) Top retrieved sample Top 3 classified Samples Using-LCEC Reterived Sample-LCEC (a) (b) Figure 23: (a) Top 3- classification for LCEC Based coding (b) Top retrieved sample The retrival system observations are presented in figure 20-23. The original test sample is shown in figure 19. For The retrival operation for a edge based coding is presented in figure 20 (a),(b). A canny edge operator is used to derive the edge informations [1], and features are drived based on the obtained edge region to retrive informations.The top three classifed observation and the best match retreival is shown in figure 20 (a) and (b) respectively. Figure 21(a) shows the top retrival resutls obtained for Contour based [4,5] approach, and the top retrieval is hown in figure 21(b). For the MCC [6] based aprpoach, the observtiosn are shown in figure 22(a) and (b) respectively. In figure 23, the retrival observations based on the proposed LCEC approach is

Empirical Coding for Curvature Based Linear Representation in Image Retrieval System DOI: 10.9790/0661-17360516 www.iosrjournals.org 15 | Page presented. From the obtained observations for the developed methods, it is observed that the proposed LCEC based approach retrieve better retrieval performance than the conventional approaches. This is obtained due to an inclusion of finer variation details in LCEC. Due to two variations selection process, the curvature of higher density are recorded as in MCC, however in the 2nd IMF selection, the second level curvature coefficients were also selected for feature description, which are totally discarded in all previous methods. This 2 level curvature selection results in higher retrieval accuracy. To evaluate the retrieval efficiency of the developed approach, the performance measures of recall and precision is made. The recall and the precision factor are derived from [10, 11], where the recall is defined as a ratio of number of relevant image retrieved over, total number of relevant image present. The Precision is derived as a ratio of number of relevant images retrieved to the total number of images retrieved. The recall and the precision factor are defined as; retrievedimagesofNo.. retrievedimagesrelevantofNo.. Precesion  presentimagesrelevantofNo.. retrievedimagesrelevantofNo.. Recall  The obtained recall over precision observation for different test observations is presented in below table I 10 20 30 40 50 60 70 80 40 50 60 70 80 90 100 Recall rate (%) Precission(%) EDge [1] Contour [4,5] MCC[6] LCEC-proposed Table I: Observation of recall v/s precision for Figure 24: Recall-Precision the developed system for developed system The observation obtained for the recall-precission curve for propsoed system is depicted in above figure 24. VI. Conclusion A new Linear Curvature Empirical Coding (LCEC) approach using Empirical Mode Decomposition for shape feature descriptor is proposed. The approach of linear representation of multiple signals is developed, wherein the curvature coefficient at different level of smoothening factor is aggregated to perform a linearization operation. In the process a spectral feature representation based on power spectral decomposition is developed. A selection criterion of IMFs for the feature extraction is proposed. From the obtained observations the recall rate of the proposed system is observed to be improved, due to finer feature information incorporated in the feature description. References [1] Hankyu Moon, Rama Chellappa, and Azriel Rosenfeld, Optimal Edge-Based Shape Detection, IEEE Transactions on Image Processing, Vol. 11, No. 11, November, 2002. [2] Ken Chatfield, James Philbin, Andrew Zisserman, Efficient retrieval of deformable shape classes using local self-similarities, proc. 12th international conference on computer vision workshops, IEEE ,2009. [3] Ye Mei and Dimitrios Androutsos, Robust affine invariant region-based shape descriptors: The ICA zernike moment shape descriptor and the whitening Zernike moment shape descriptor,” IEEE signal processing, Vol. 16, No. 10, October 2009. [4] Jamie Shotton, Andrew Blake, Roberto Cipolla, Contour-Based Learning for Object Detection”, Proc.10th International Conference on Computer Vision, IEEE, 2005. [5] Xiang Baia, Xingwei Yang, Longin Jan Latecki, Detection and recognition of contour parts based on shape similarity, Pattern recognition, Elsevier 2008. [6] Livari Kunttu, Leena Lepisto, Juhani Rauhamaa and Ari Visa, Multiscale Fourier descriptor for shape-based image retrieval, Proc. International conference on pattern recognition 2004. [7] B. Zhong and W. Liao, Direct curvature scale space: theory and corner detection, IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 29, no. 3, pp. 508–512, 2007.

Empirical Coding for Curvature Based Linear Representation in Image Retrieval System DOI: 10.9790/0661-17360516 www.iosrjournals.org 16 | Page [8] Y. Cui and B. Zhong, Shape retrieval based on parabolically fitted curvature scale-space maps, Intelligent Science and Intelligent Data Engineering, vol. 7751 of Lecture Notes in Computer Science, pp.743–750, 2013. [9] Y. Gao, G. Han, G. Li, Y.Wo, and D.Wang, Development of current moment techniques in image analysis, Journal of Image and Graphics, vol. 14, no. 8, pp. 1495–1501, 2009. [10] Mehul P. Sampat, Zhou Wang, Shalini Gupta, Alan Conrad Bovik and Mia K. Markey, Complex wavelet structural similarity: A new image similarity index, IEEE transactions on image processing, Vol. 18, No. 11, November 2009. [11] Suhas G. Salve, Kalpana C. Jondhale, Shape matching and object recognition using shape contexts, Proc. IEEE 2010. [12] Sergie Belongie, Jitendra Malik and Jan Puzicha, Shape matching and object recognition using shape contexts, IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002. [13] Dengsheng Zhang, Guojun Lu, Review of shape representation and description techniques, Pattern recognition, Elsevier, 2004. [14] Gul-e-Saman, S. Asif, M. Gilani, Object recognition by modified scale invariant feature transform, Proc. 3rd international workshop on semantic media adaptation and personalization, 2008. [15] Sadegh Abbasi, Farzin Mokhtarian, Josef Kittler, Curvature scale space image in shape similarity retrieval, Multimedia Systems 7: 467–476, Springer, 1999. [16] Donghoh Kim and Hee-Seok Oh, EMD: A Package for Empirical Mode Decomposition and Hilbert Spectrum, The R Journal Vol. 1,1, May 2009. [17] Navin Chatlani and John J. Soraghan, EMD-Based Filtering (EMDF) of Low-Frequency Noise for Speech Enhancement, IEEE Transactions on Audio, Speech, and Language Processing, Vol. 20, No. 4, May 2012. [18] Konstantinos Ioannidis and Ioannis Andreadis, A Digital Image Stabilization Method Based on the Hilbert–Huang Transform, IEEE Transactions on Instrumentation and Measurement, Vol. 61, No. 9, September 2012. [19] Jeffery C. Chan, Hui Ma, Tapan K. Saha and Chandima Ekanayake, Self-adaptive Partial Discharge Signal De-noising Based on Ensemble Empirical Mode Decomposition and Automatic Morphological Thresholding, IEEE Transactions On Dielectrics and Electrical Insulation, 21 1: 294-303, 2014. [20] Piotr Dudek, David Lopez Vilarino, A Cellular Active Contours Algorithm Based on Region Evolution, Proc. International Workshop on Cellular Neural Networks and Their Applications, IEEE, 2006. [21] Tian Qiu, Yong Yan, and Gang Lu, An Autoadaptive Edge-Detection Algorithm for Flame and Fire Image Processing, IEEE Transactions on Instrumentation and Measurement, Vol. 61, No. 5, May 2012. [22] Dayanand Jamkhnadikar, V.D. Mytri, CSS based Trademark retrieval system, Proc. of International Conference on Electronic Systems, Signal Processing and Computing Technologies IEEE 2014 pp 129-133. [23] http://zoi.utia.cas.cz/tree_leaves

Empirical Coding for Curvature Based Linear Representation in Image Retrieval System

More Related Content

What's hot

Viewers also liked

Similar to Empirical Coding for Curvature Based Linear Representation in Image Retrieval System

More from iosrjce

Recently uploaded

Empirical Coding for Curvature Based Linear Representation in Image Retrieval System