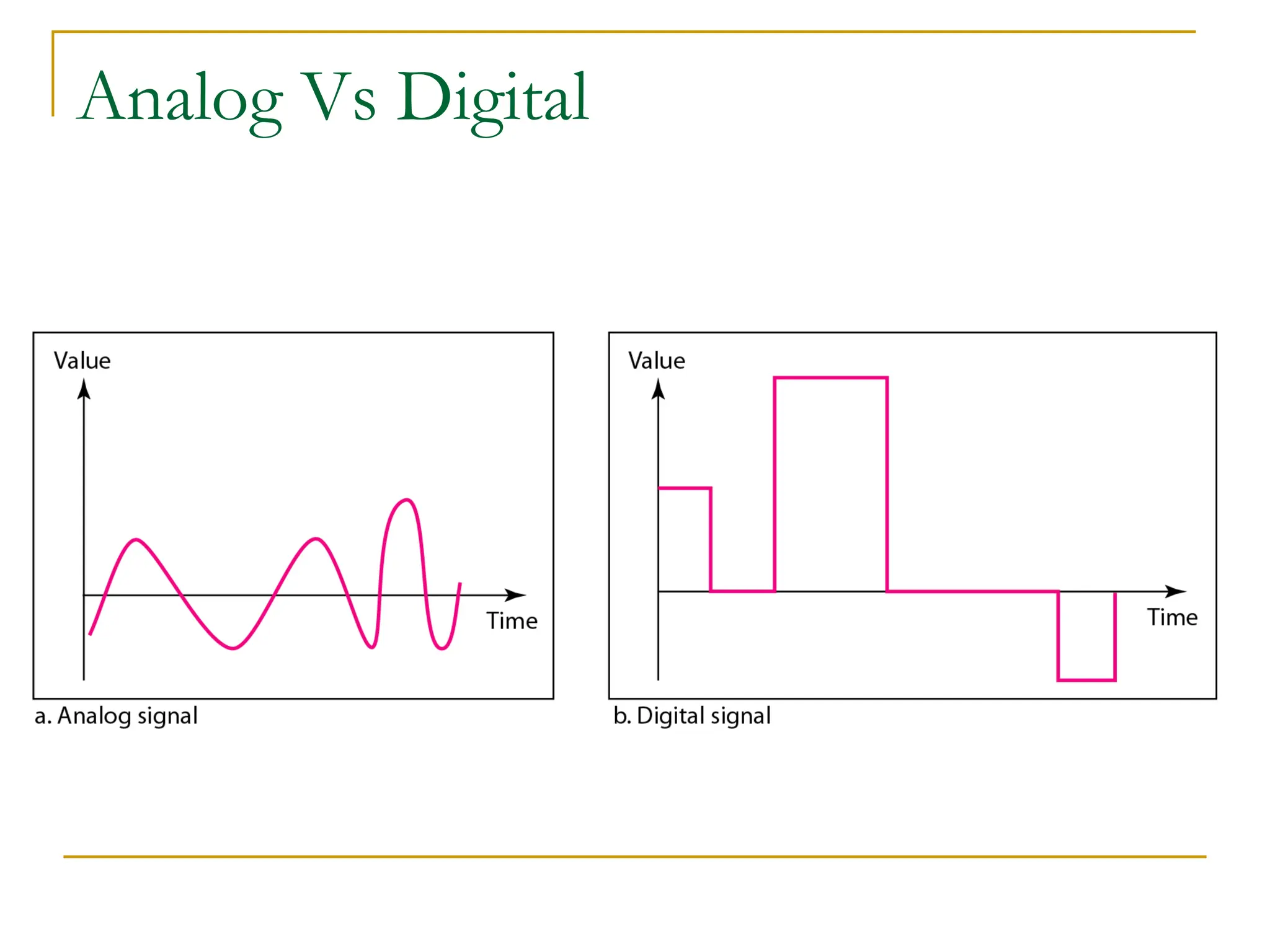
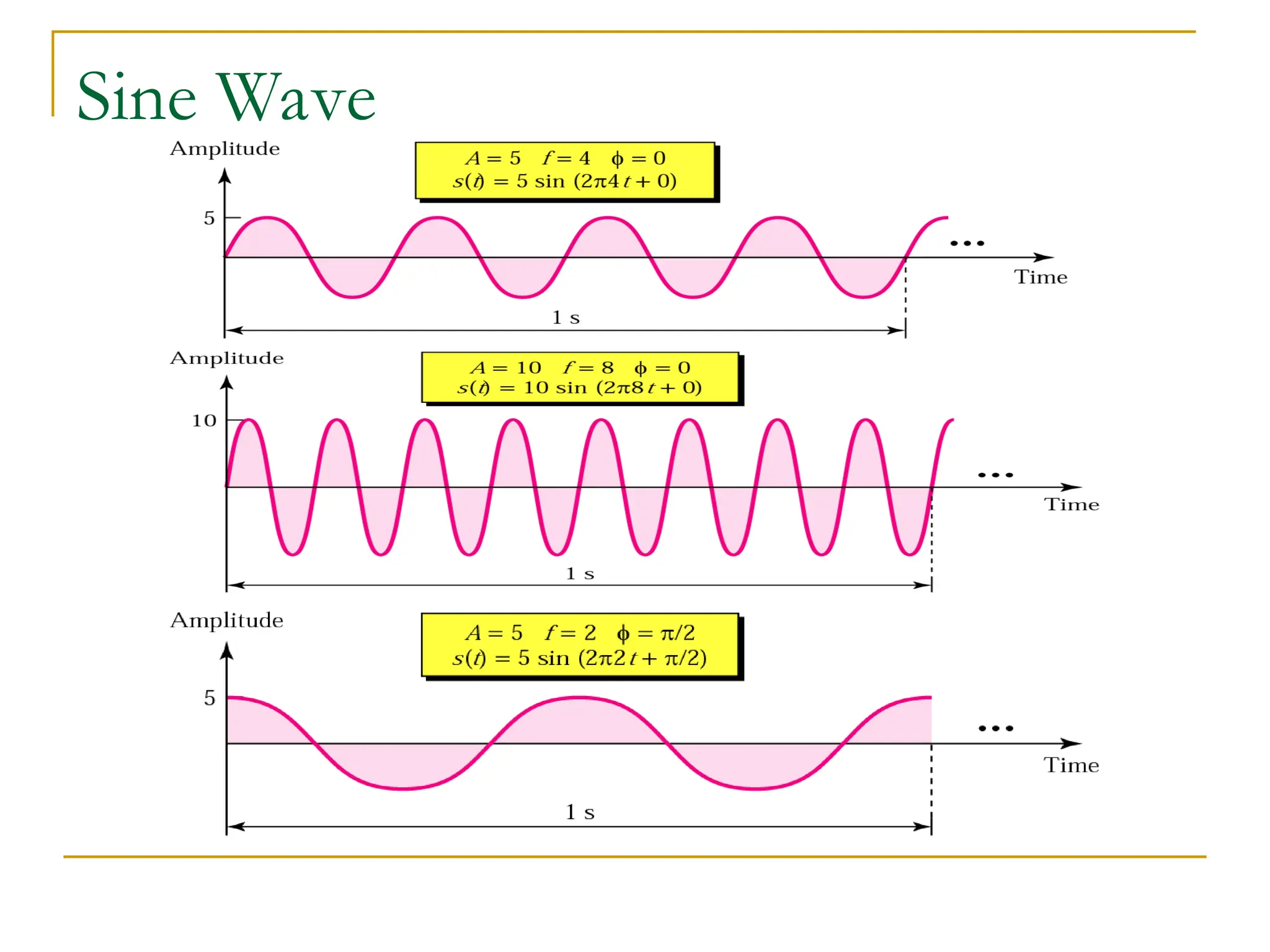
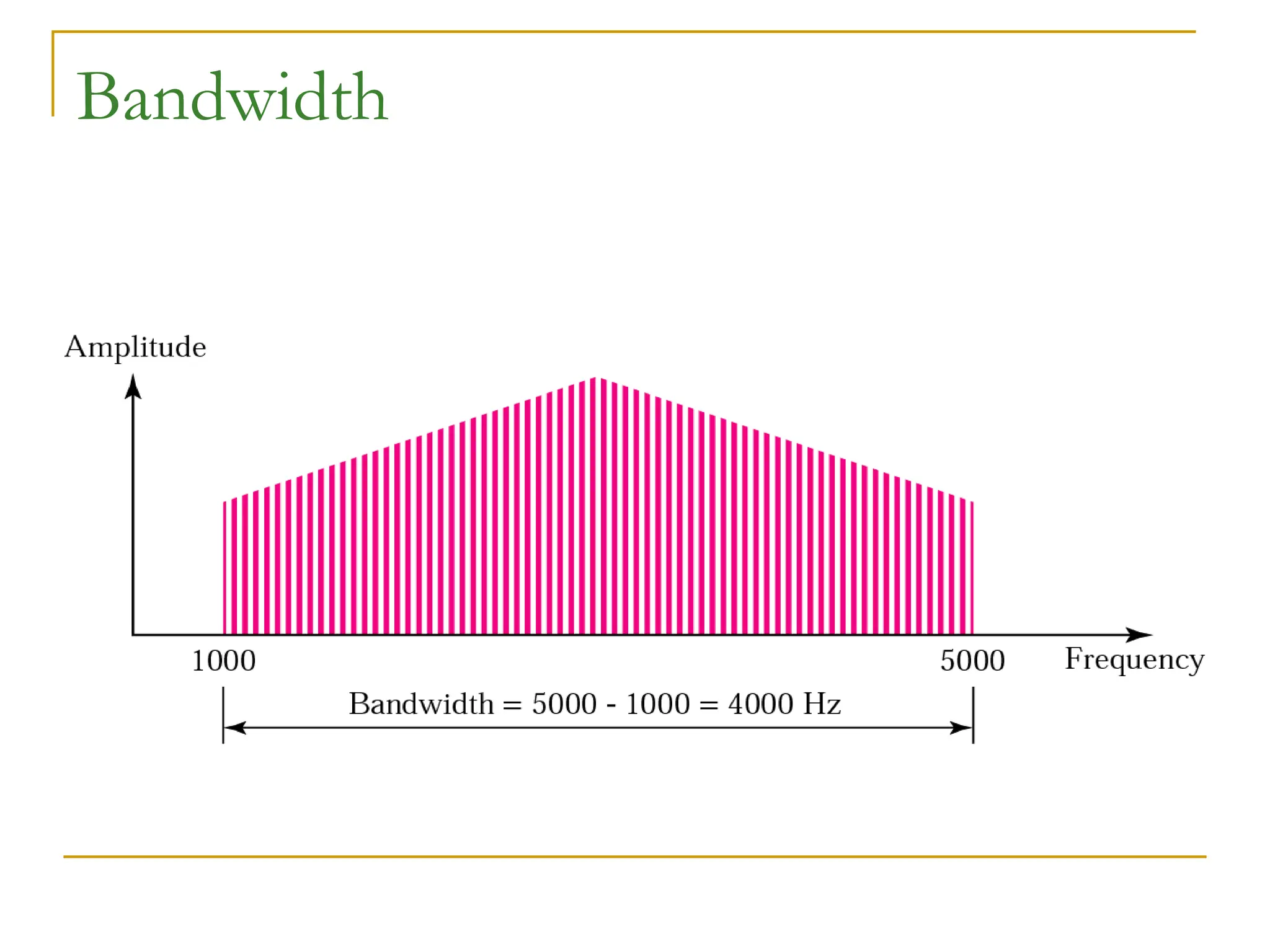
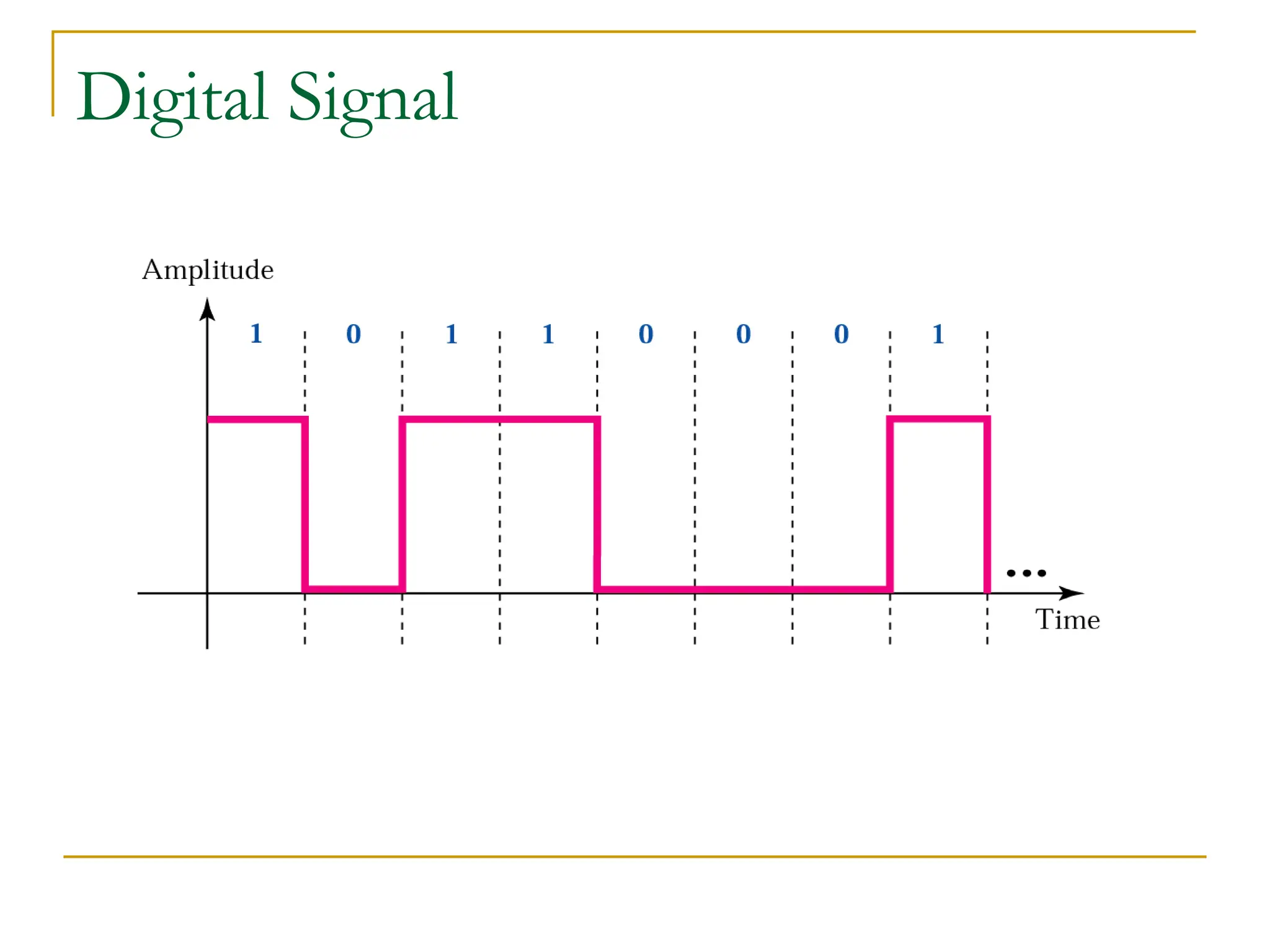
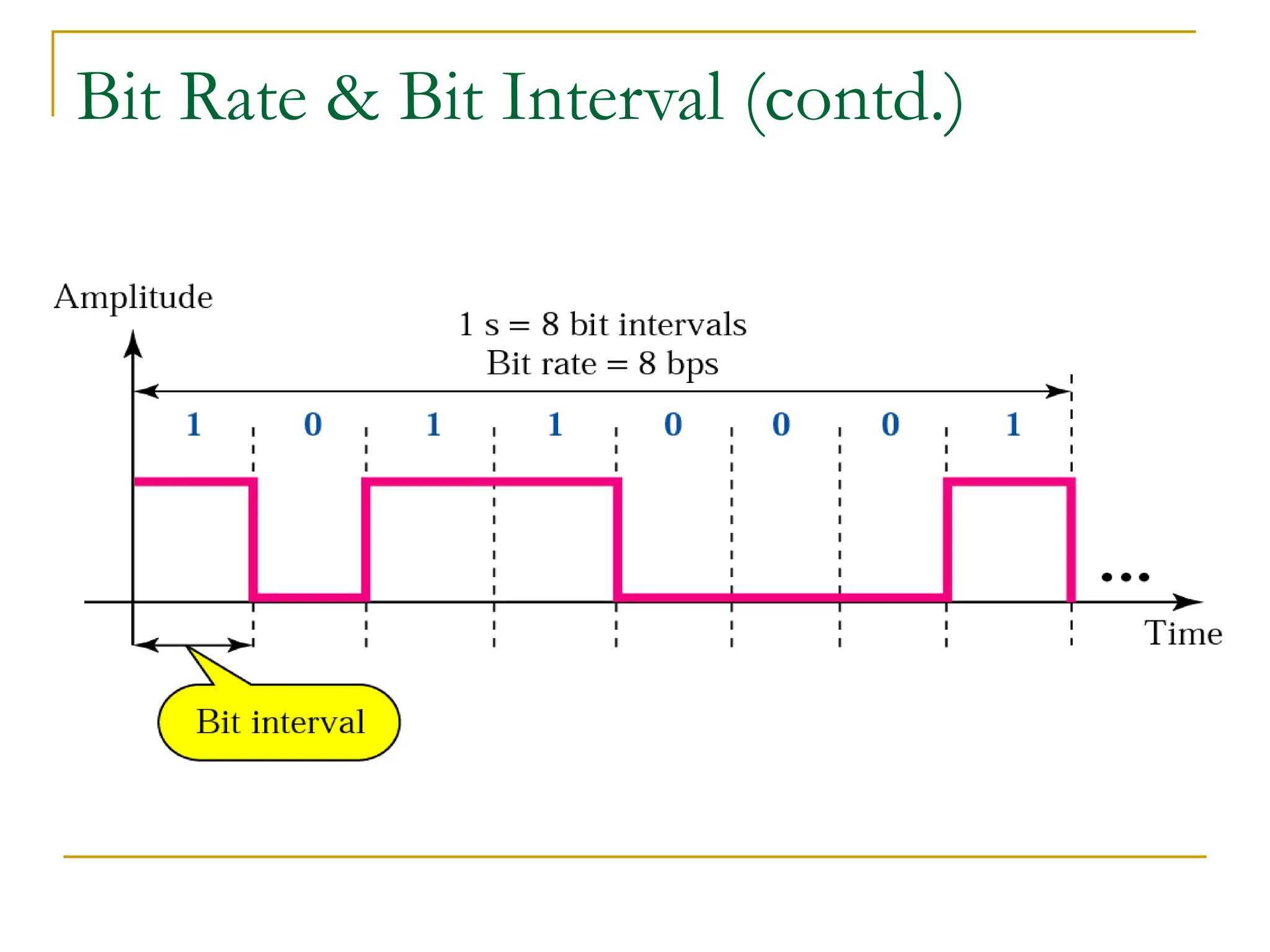
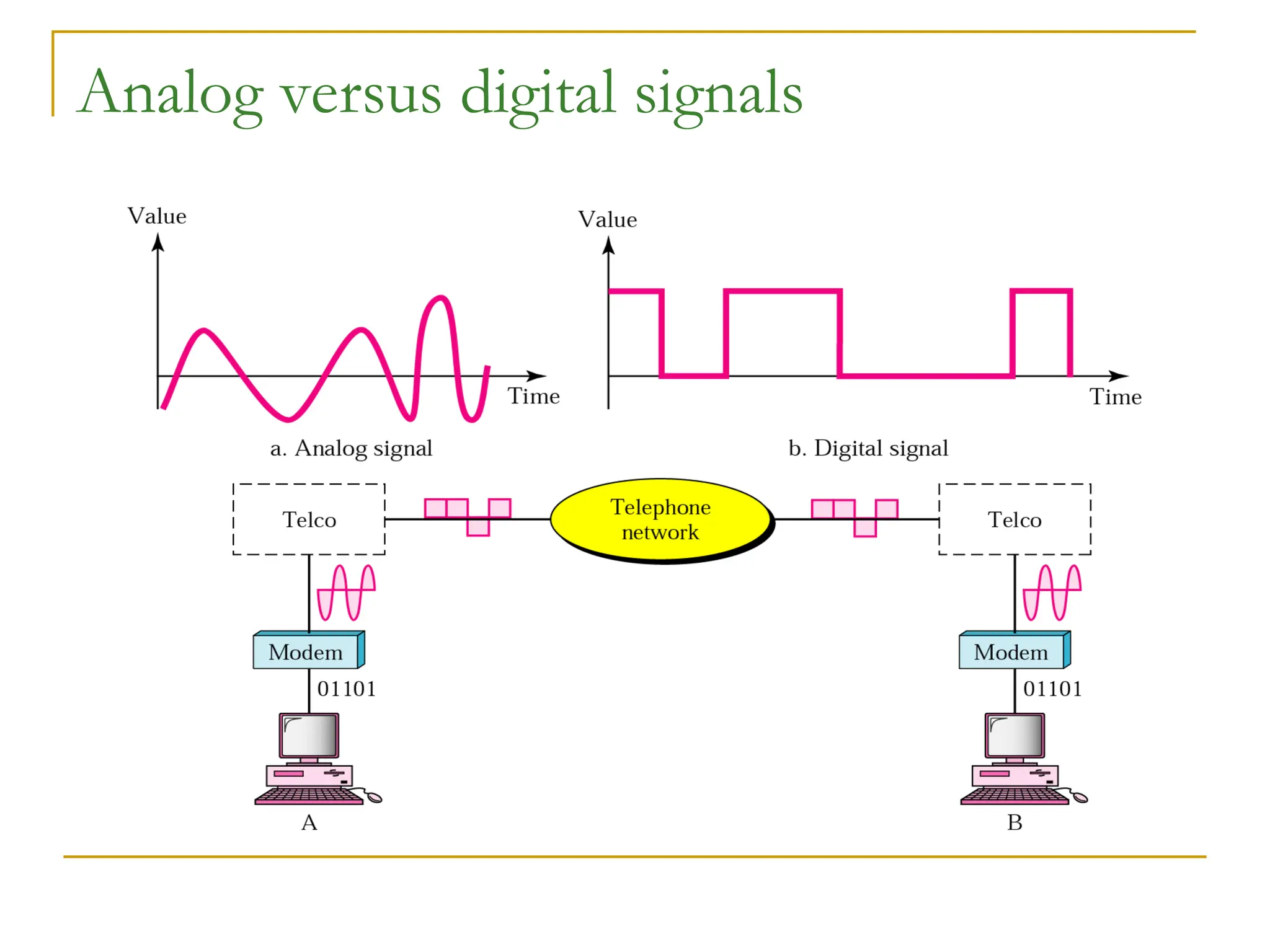
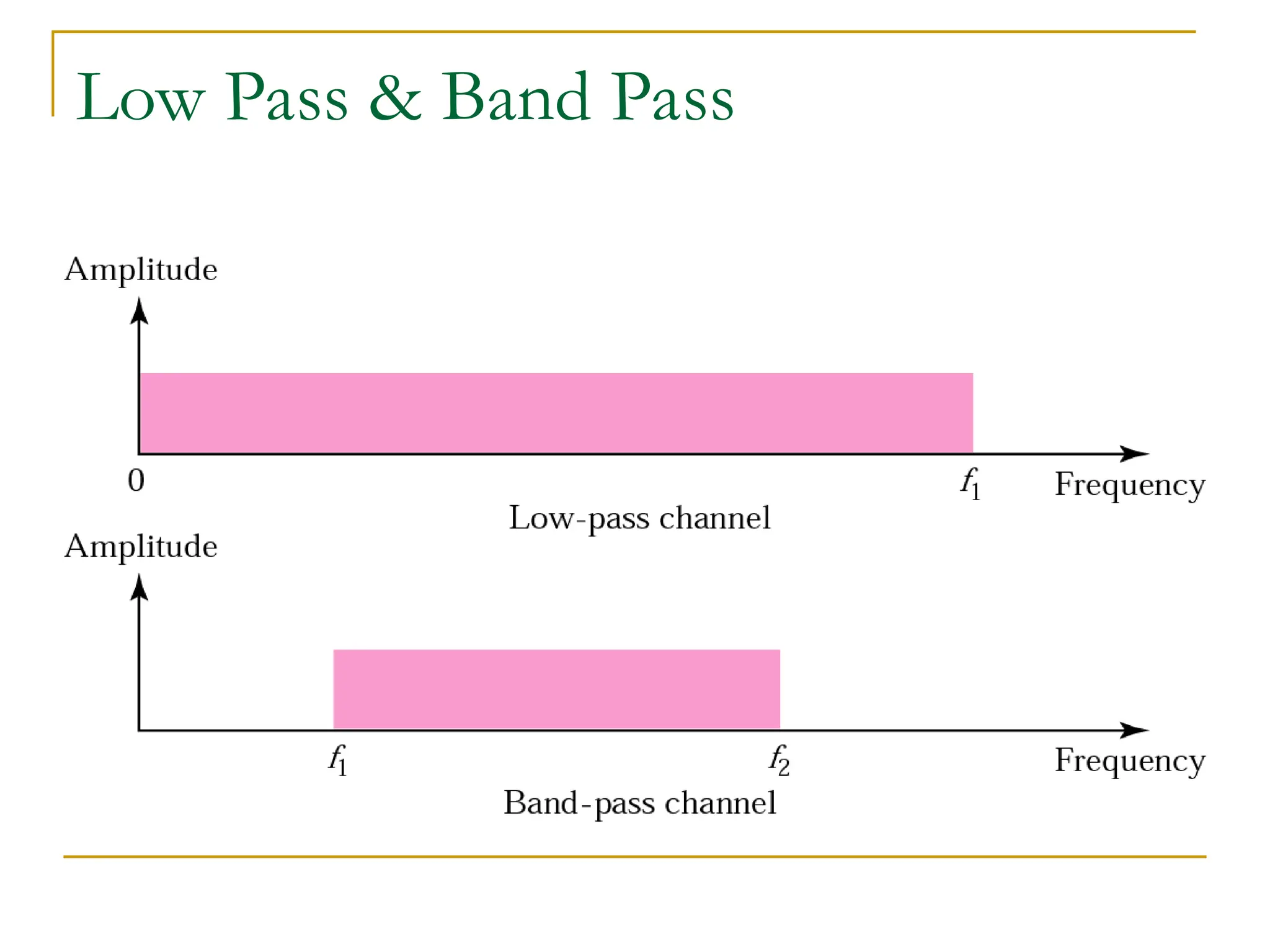
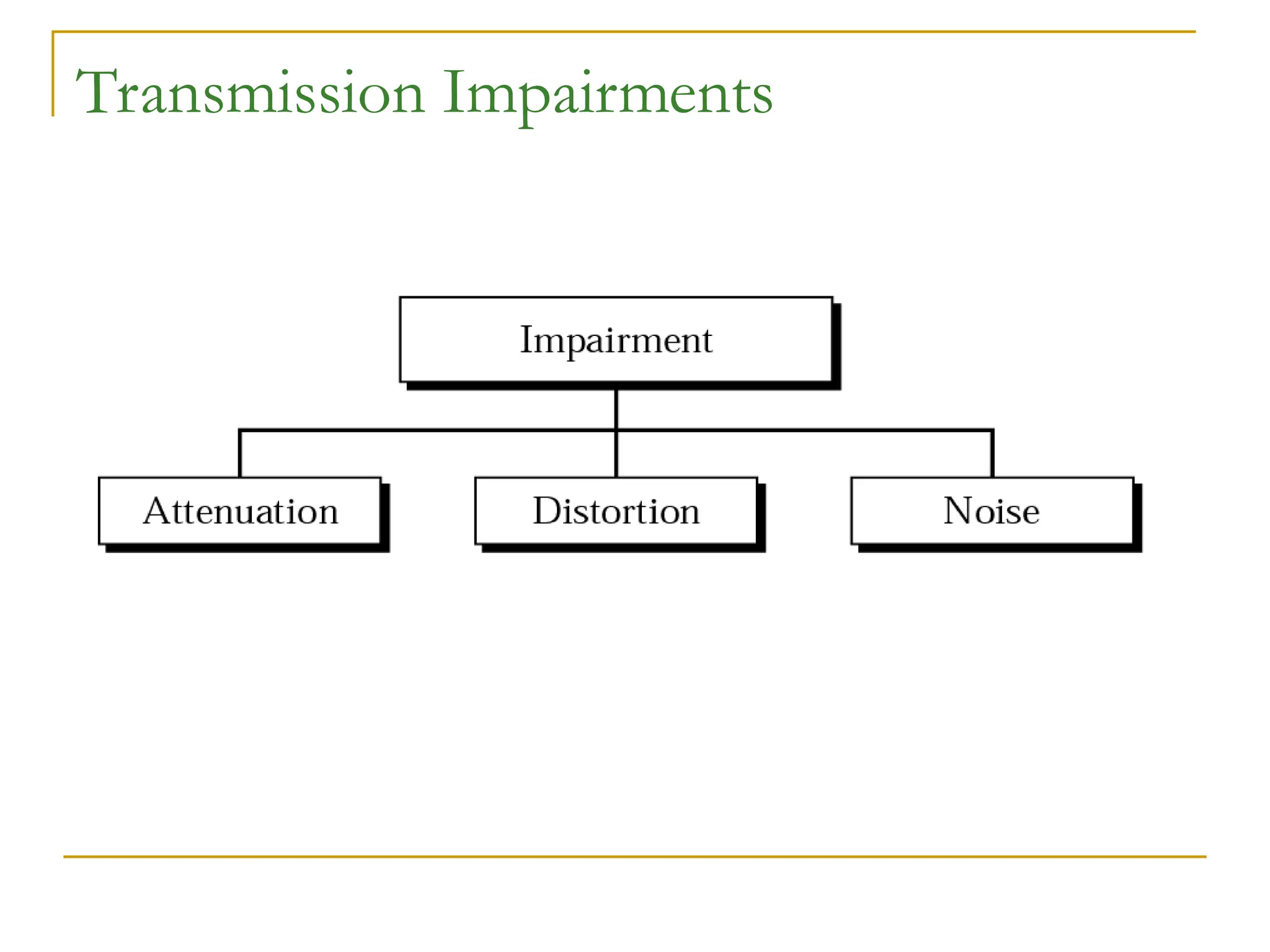
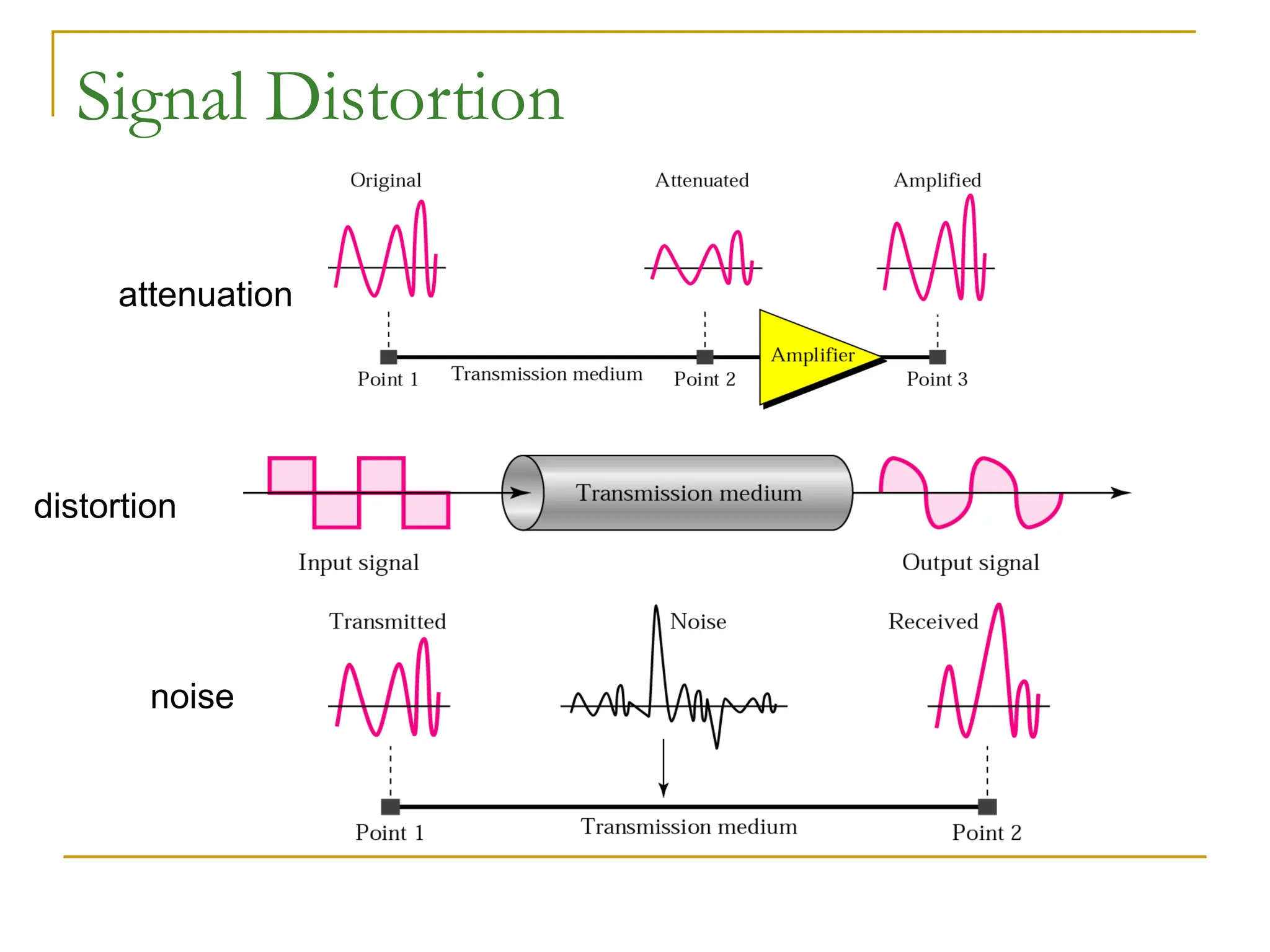
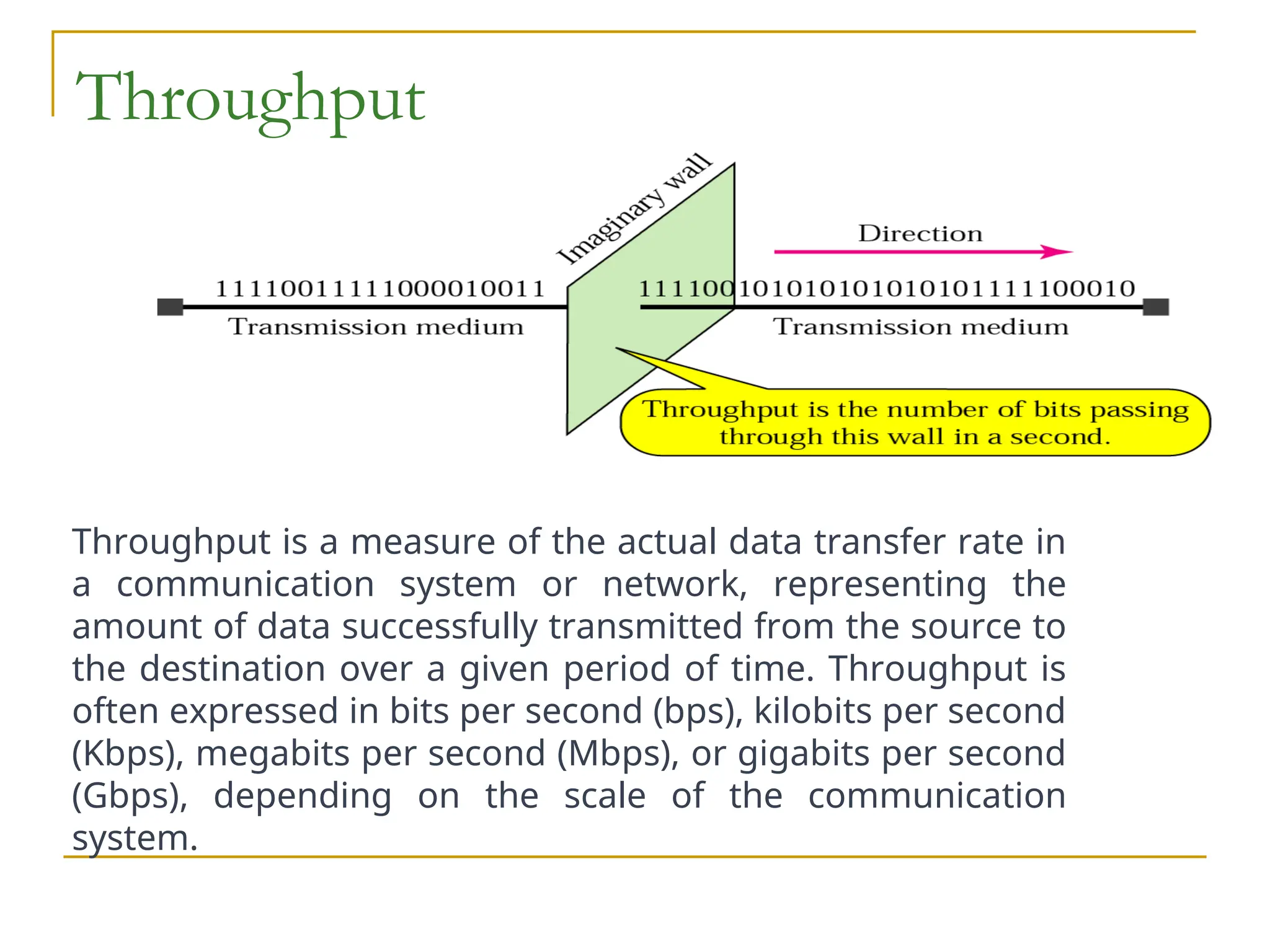
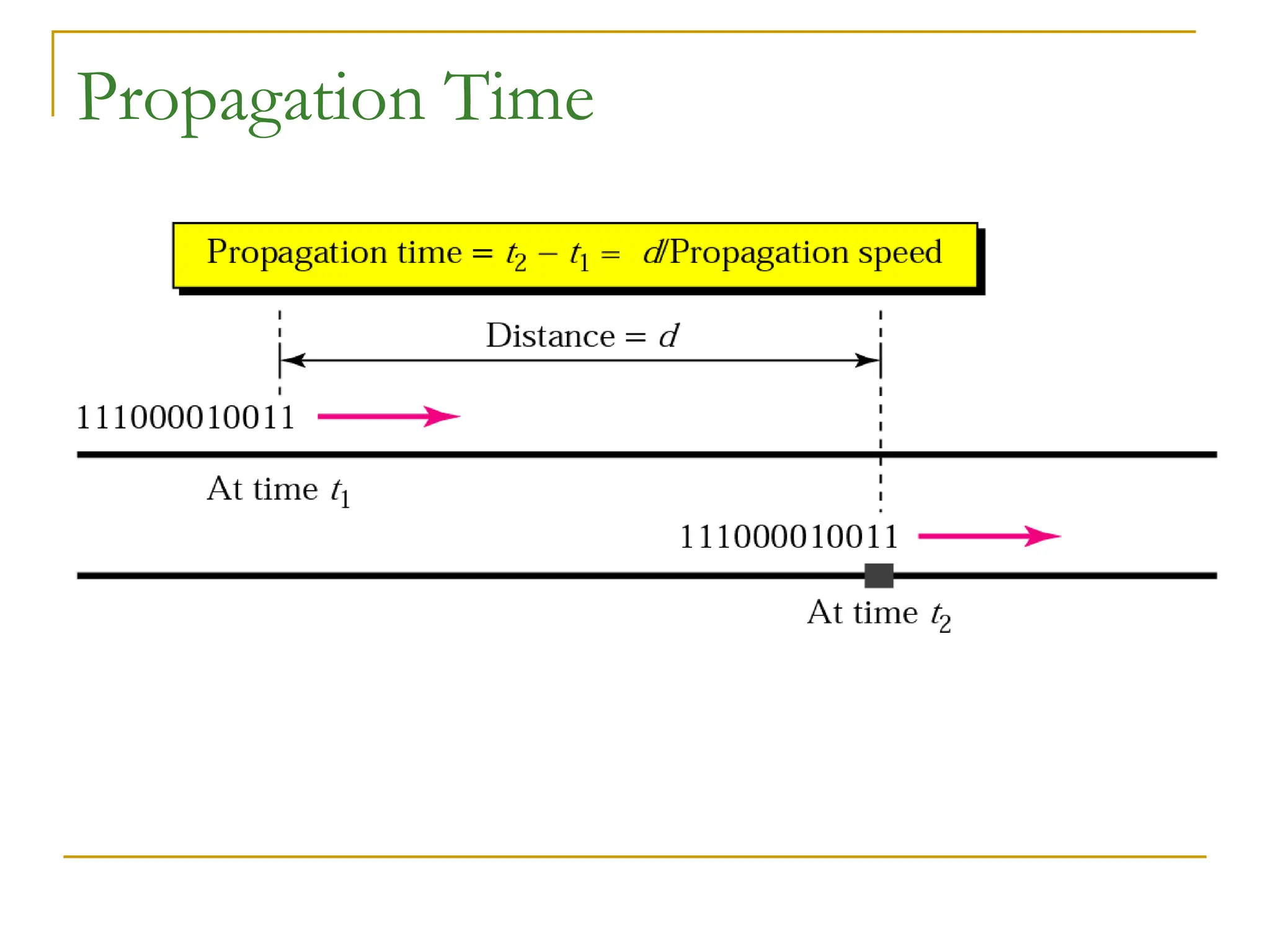
The document discusses the physical layer of data communication, covering concepts such as analog and digital data transmission, signal representation, and the factors affecting data rates over a communication channel. It details the Nyquist bit rate for noiseless channels and Shannon capacity for noisy channels, emphasizing the importance of bandwidth, signal levels, and signal-to-noise ratio. Additionally, it addresses transmission impairments and network performance metrics, including throughput and latency.